中值定理
一、罗尔定理
定理3.1 若函数f(x)满足条件:
1)在[a,b]上连续;
2)在(a,b)内可导;
3)在区间端点处的函数值相等,即f(a)=f(b);
则在(a,b)内至少存在一点ξ,使得f′(ξ)=0.
证 如图3-1所示,因为f(x)在[a,b]上连续,由连续函数的性质,f(x)在[a,b]上必有最大值M和最小值m.
1)如果m=M,则f(x)在[a,b]上恒为常数M,因此在(a,b)内恒有f(x)=M,于是,在整个区间(a,b)内恒有f′(x)=0,(a,b)内每一点都可取为ξ,定理成立.
2)如果m<M,因为f(a)=f(b),则M与m中至少有一个不等于端点a处的函数值f(a),设M≠f(a)(如果设m≠f(a),证法完全类似),从而,在(a,b)内至少有一点ξ,使得f(ξ)=M.下面证明f′(ξ)=0.
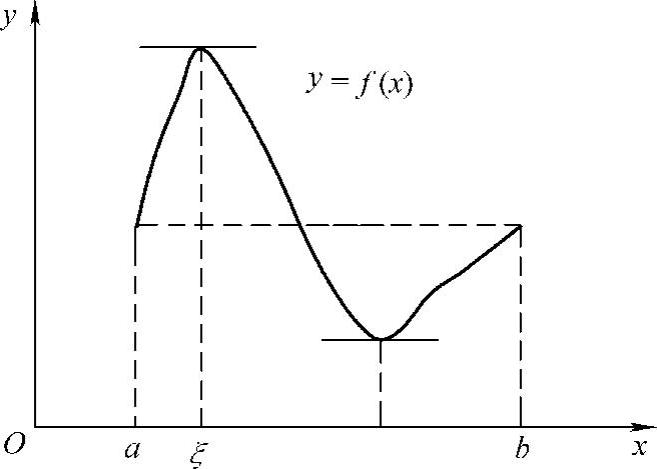
图3-1
事实上,因为f(ξ)=M是最大值,所以不论Δx为正或负,只要ξ+Δx∈(a,b),恒有f(ξ+Δx)≤f(ξ),由f(x)在ξ点可导的条件及极限的保号性
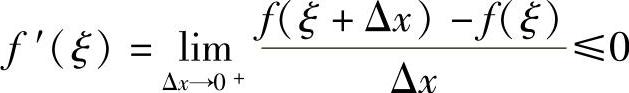
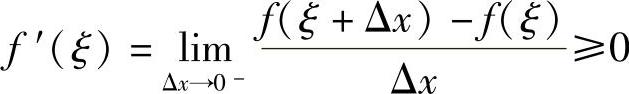
因此必有f′(ξ)=0.
定理的几何意义为,设有一段连续曲线,它的两端点的高度相等,且除两端点外,曲线上处处都有不垂直于x轴的切线,则曲线上至少有一点处的切线平行于x轴.
例1 不求出函数f(x)=(x-1)(x-2)(x-3)(x-4)的导数,说明方程f′(x)=0有几个实根,并指出它们所在的区间.
解 因为f(x)=(x-1)(x-2)(x-3)(x-4)在[1,4]上可导,且
f(1)=f(2)=f(3)=f(4),所以f(x)在[1,2],[2,3],[3,4]上满足罗尔定理的条件.因此f′(x)=0至少有三个实根,分别位于区间(1,2)、(2,3)、(3,4)内.
又因为f′(x)是三次多项式,故f′(x)=0至多有三个实根,于是方程f′(x)=0恰有三个实根,分别位于区间(1,2),(2,3),(3,4)内.
二、拉格朗日定理
定理3.2 若函数f(x)满足条件:
1)在[a,b]上连续;
2)在(a,b)内可导.则至少存在一点ξ∈(a,b)使得
f(b)-f(a)=f′(ξ)(b-a)
即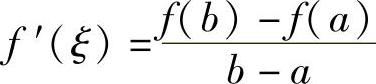 .
.
如图3-2所示,定理的几何意义是: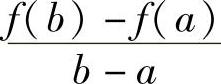 是割线AB的斜率,而f′(ξ)是曲线y=f(x)在点C(ξ,f(ξ))处的切线的斜率.拉格朗日定理的意义是:若区间[a,b]上有一条连续曲线,曲线上每一点都有切线,则曲线上至少有一点C(ξ,f(ξ)),过C点的切线与割线
是割线AB的斜率,而f′(ξ)是曲线y=f(x)在点C(ξ,f(ξ))处的切线的斜率.拉格朗日定理的意义是:若区间[a,b]上有一条连续曲线,曲线上每一点都有切线,则曲线上至少有一点C(ξ,f(ξ)),过C点的切线与割线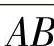 平行.
平行.
证 由几何意义可知,罗尔定理是拉格朗日定理的特殊情况,
为此,构造一个辅助函数F(x)=(b-a)f(x)-[f(b)-f(a)]x.可知F(x)在[a,b]上连续,且在(a,b)内可导.
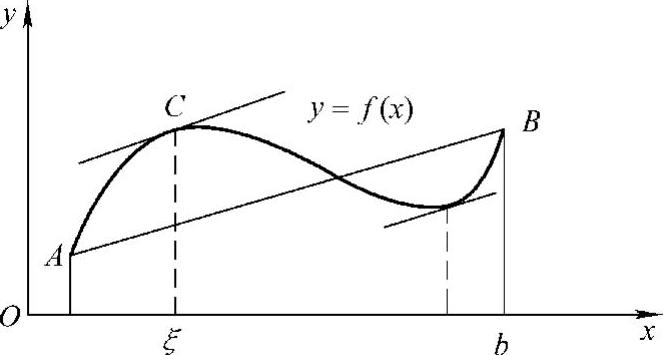
图3-2
又因为F(b)=bf(a)-af(b)=F(a),从而F(x)满足罗尔定理的条件,则在(a,b)内至少存在一点ξ,使得F′(ξ)=0.
即f(b)-f(a)=f′(ξ)(b-a)或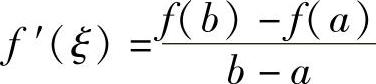 .
.
由a<ξ<b,可得ξ=a+θ(b-a)(0<θ<1)(https://www.daowen.com)
所以,拉格朗日中值定理又可写成:
f(b)-f(a)=f′[a+θ(b-a)]·(b-a)(0<θ<1),
称之为拉格朗日中值定理的有限增量形式.
例2 证明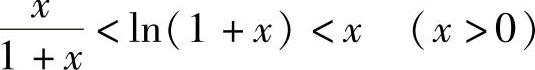 .
.
证 设f(x)=ln(1+x),则f(x)在[0,x]上满足拉格朗日中值定理的条件,且
f(x)-f(0)=f′(ξ)(x-0),(0<ξ<x)
即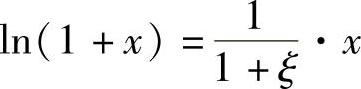 ,又因为
,又因为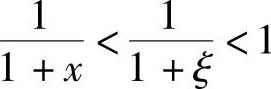 ,且x>0,从而得
,且x>0,从而得
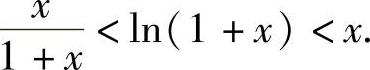
推论3.1 若函数f(x)在区间(a,b)内的导数恒为零,则函数f(x)在区间(a,b)内恒为常数.
证 在区间(a,b)内任意取两点x1和x2,设x1<x2,则f(x)在区间[x1,x2]上满足拉格朗日中值定理的条件,则有
f(x2)-f(x1)=f′(ξ)(x2-x1)ξ∈(x1,x2)
由已知,f′(ξ)=0,可得f(x1)=f(x2),
因此,区间(a,b)内任意两点的函数值相等,即函数f(x)在区间(a,b)内恒为常数.
推论3.2 若函数f(x)和g(x)在区间(a,b)内的导数都相等,则函数f(x)和g(x)在区间(a,b)内至多相差一个常数.
证 设F(x)=f(x)-g(x),由推论3.1可知在区间(a,b)内,
F(x)=C,即f(x)=g(x)+C.
例3 证明: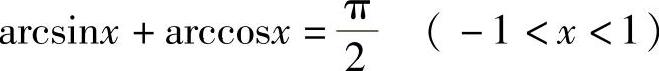 .
.
证 对于任意给定的x∈(-1,1),有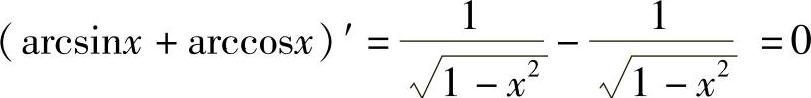 .
.
从而由推论3.1可知,
arcsinx+arccosx=C (C为常数).
又令x=0,得
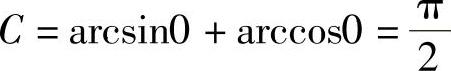 ,
,
即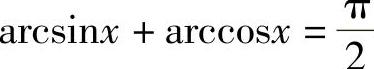 .
.
三、柯西中值定理
定理3.3 若函数f(x)与g(x)满足条件:
1)在闭区间[a,b]上连续;
2)在开区间(a,b)内可导;
3)对任意x∈(a,b),有g′(x)≠0;则至少存在一点ξ∈(a,b)使得
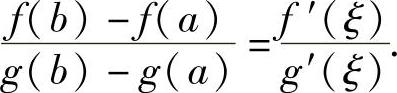
证 首先,可以推出g(b)-g(a)≠0.否则,若g(b)=g(a),则由罗尔定理可知,在(a,b)内至少存在一点ξ,使得g′(ξ)=0,这与条件3)矛盾.
作辅助函数F(x)=[f(b)-f(a)]g(x)-[g(b)-g(a)]f(x),有F(x)在[a,b]上连续,且在(a,b)内可导,
F(a)=g(a)f(b)-g(b)f(a)=F(b).
因此,F(x)满足罗尔定理的条件,则在(a,b)内至少存在一点ξ,使得F′(ξ)=0,即 [g(b)-g(a)]·f′(ξ)-[f(b)-f(a)]·g′(ξ)=0,从而有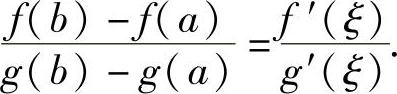
特别地,当g(x)=x时,柯西中值定理就变成拉格朗日中值定理.
