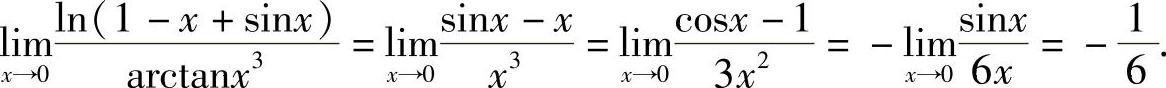洛必达法则
在求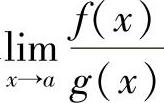
或
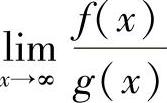时，若发现f（x）和g（x）同时趋于0，或同时趋于∞，如
，
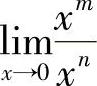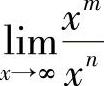，则上述极限可能存在，也可能不存在.要根据具体的函数来进一步确定，通常把这种极限称为
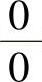或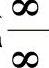
型的未定式，这种未定式是不能用商的极限运算法则来计算的.在这一节中，可以利用洛必达法则来解决这类问题.
一、“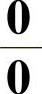
”型未定式
定理3.4 （洛必达法则）设函数f（x）和g（x）满足条件：
1）
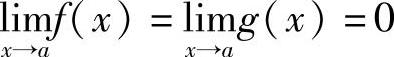；2）在点a的某个去心邻域U°（a）内都可导，且g′（x）≠0；3）
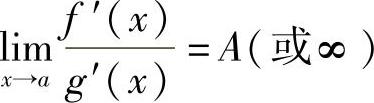；则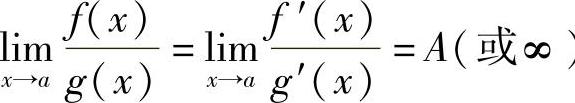
）.
证 在点x=a处补充定义f（x）=g（x）=0，则函数f（x）与g（x）在点x=a点连续.
对任意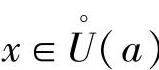
，在以x和a为端点的区间上，由柯西中值定理，则在x与a之间存在一点ξ，使得
.
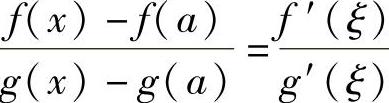又因为ξ在x与a之间，所以当x→a时，有ξ→a，上式两边取极限，得
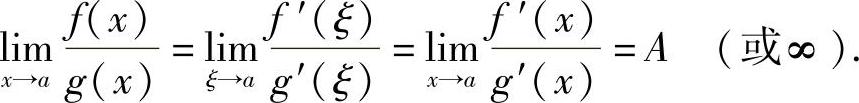
将此定理中的x→a换成其他的自变量变化过程亦成立，证明从略.
例1 求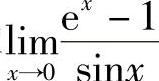
.
解 由洛必达法则，有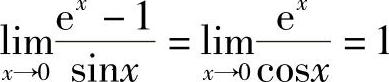
.
例2 求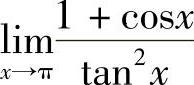
.
解 由洛必达法则，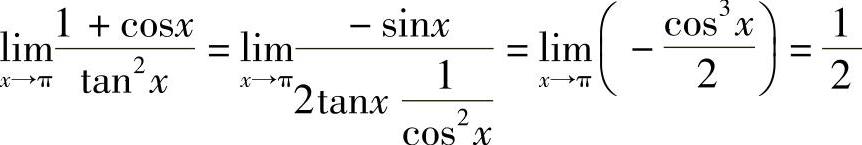
.
求一个未定式的极限时，如果一阶导数之比还是未定式，只要仍满足洛必达法则的条件，则可以再次使用洛必达法则.倘若结果还是未定式，那么还可以继续使用洛必达法则.
例3 求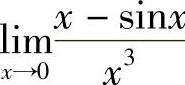
.
解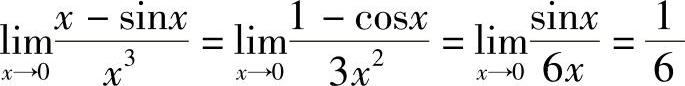 
.二、“
”型未定式
定理3.5 设函数f（x）与g（x）满足：
1）在点a的某个去心邻域U°（a）内都可导，且g′（x）≠0；2）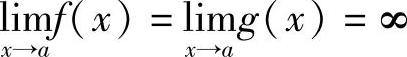
；3）
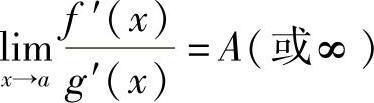；则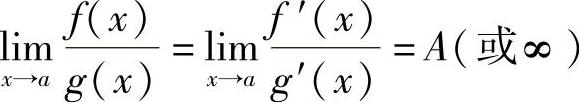
.将此定理中的x→a换成其他的自变量变化过程亦成立，证明从略.
例4 求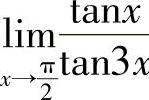
.
解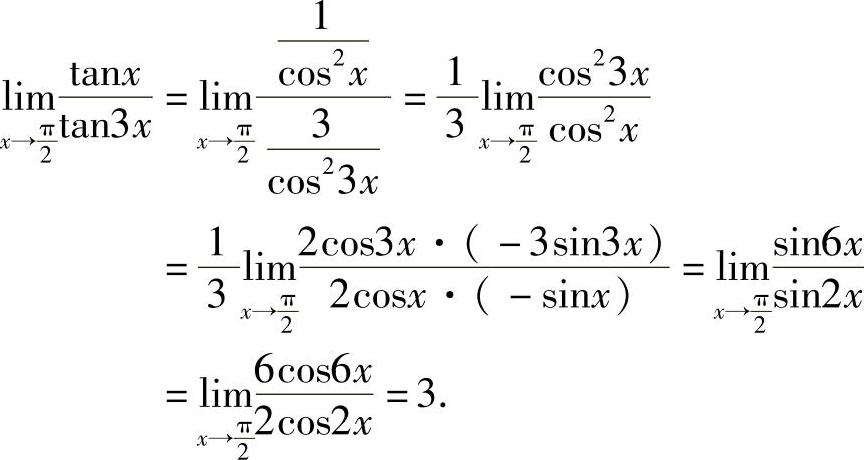 
例5 求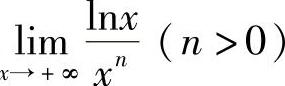
.(https://www.daowen.com)
解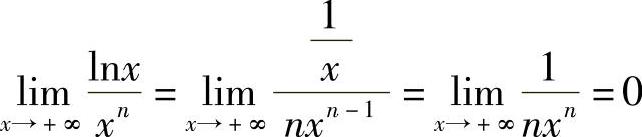 
.
例6 求极限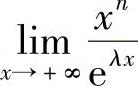
（n为正整数，λ＞0）.
解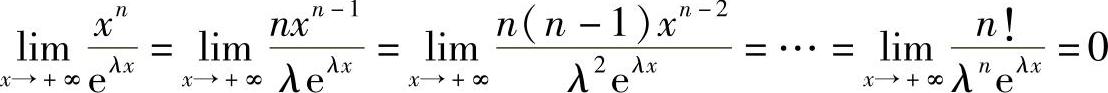 
.三、其他型未定式
例7 求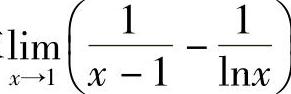
.
解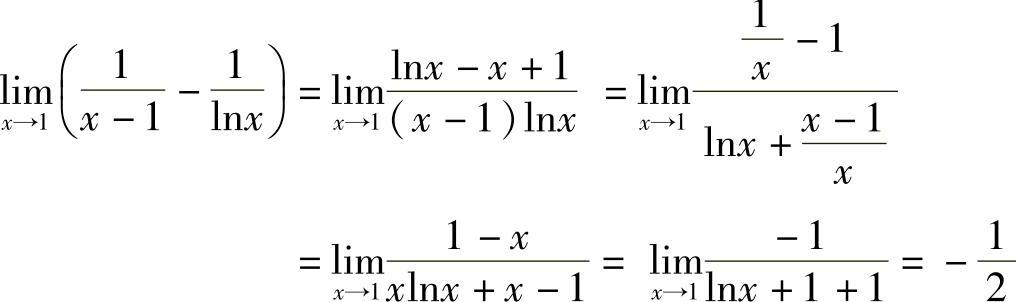 
.
例8 求极限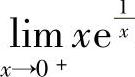
.
解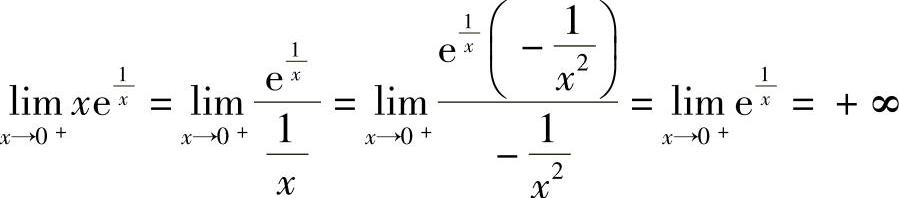 
.
例9 求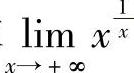
.
解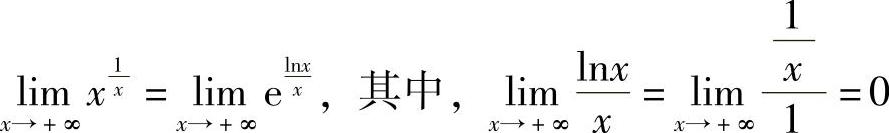 
，则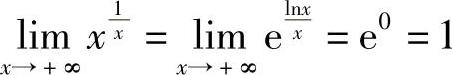
.
例10 求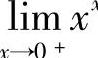
.
解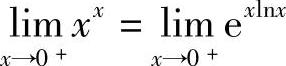 
，其中，
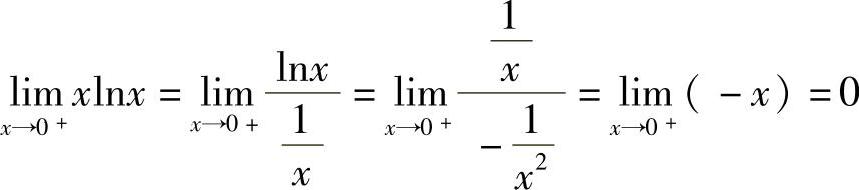，则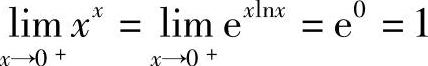
.
例11 求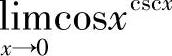
.
解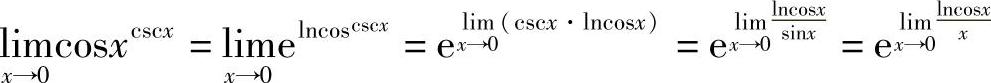
.
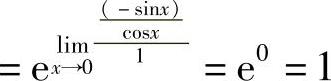例12 求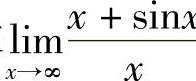
.
解 极限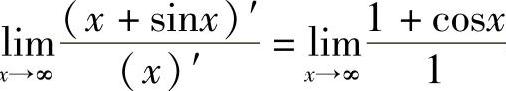
不存在，不能应用洛必达法则.实际上，
.
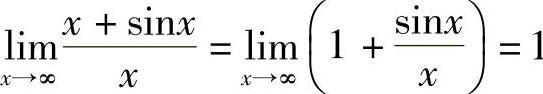例13 求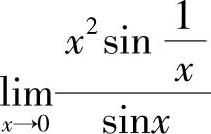
.
解 这是“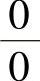
”型未定式，因极限
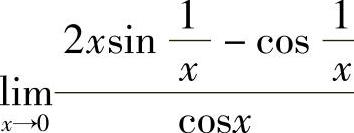不存在，所以有
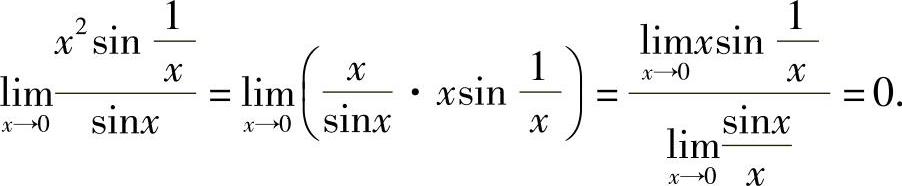
例14 求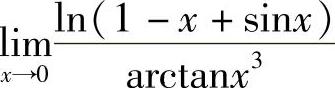
.
解 先用等价无穷小代换，再用洛必达法则.
