广义积分与Γ函数

第五节 广义积分与Γ函数

一、无穷限的广义积分

定义5.3 设函数f（x）在区间[a，+∞）上连续，取b>a，如果极限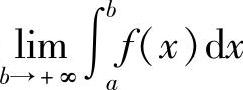存在，则称此极限值为函数f（x）在无穷区间[a，+∞）上的广义积分，记作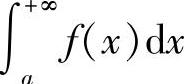，即

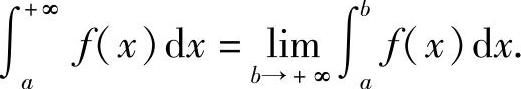
这时也称广义积分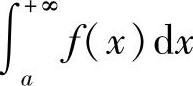收敛；反之，则称广义积分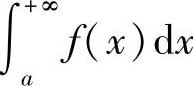发散.同样，可以定义f（x）在（-∞，b]，（-∞，+∞）上的广义积分.

定义5.4 设f（x）在区间（-∞，b]上连续，取a<b，如果极限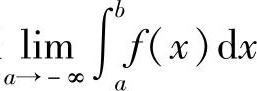存在，则称此极限值为函数f（x）在无穷区间（-∞，b]上的广义积分，记作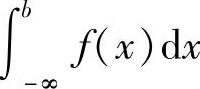，即

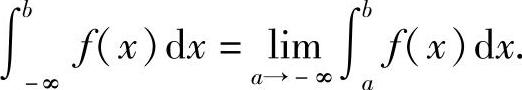
这时也称广义积分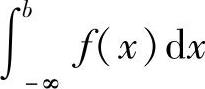收敛；反之，则称广义积分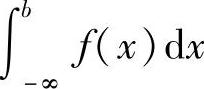发散.

定义5.5 设函数f（x）在区间（-∞，+∞）内连续，如果广义积分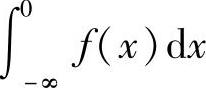和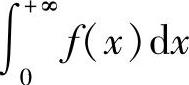都收敛，则称上述两个广义积分之和为函数f（x）在无穷区间（-∞，+∞）上的广义积分，记作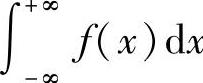，即

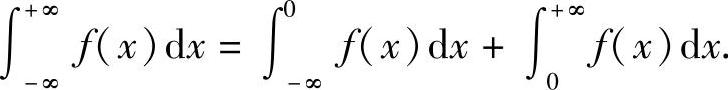
这时也称广义积分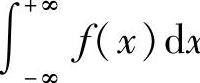x收敛；否则，就称广义积分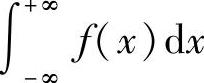发散.

设函数f（x）在[a，+∞）上连续，F（x）是f（x）的原函数，为了方便，分别记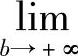[F（x）]^b_a为[F（x）]_a+∞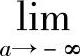，[F（x）]^b_a为[F（x）]^b-∞，则无穷限的广义积分，∞.

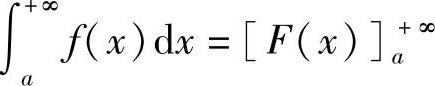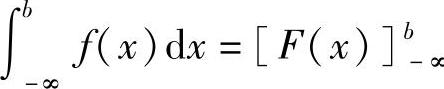例1 求，，.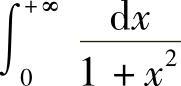

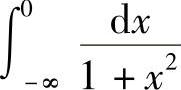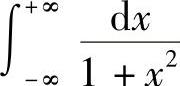解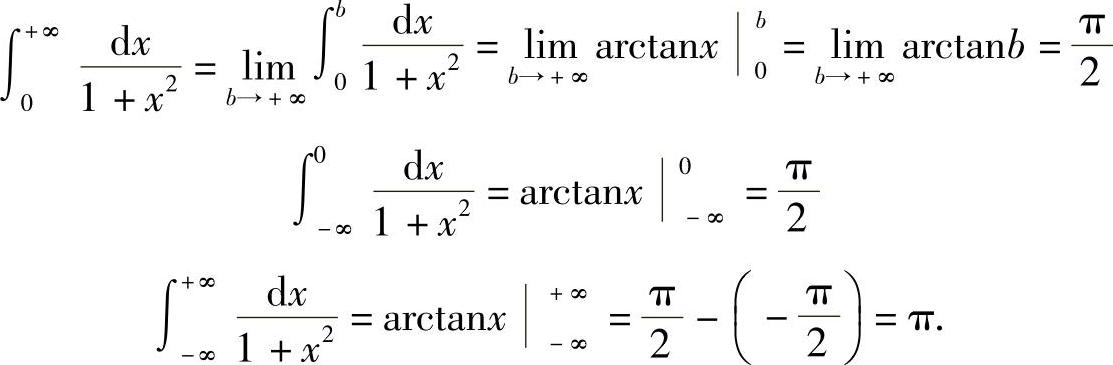

例2 求.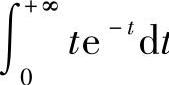

解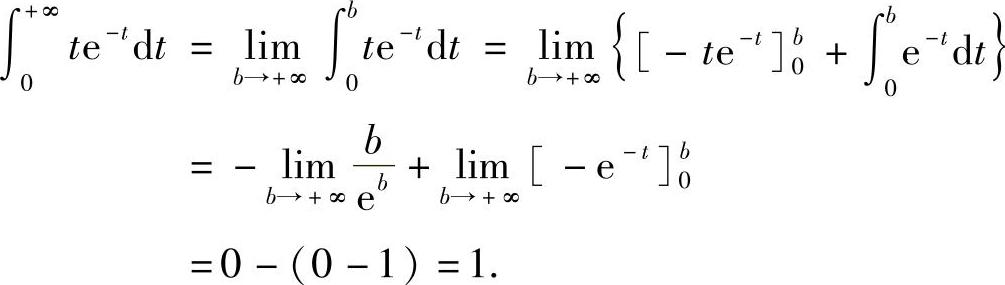

例3 讨论广义积分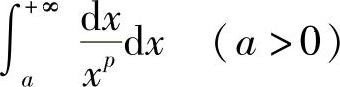的收敛性.

解 当p≠1时

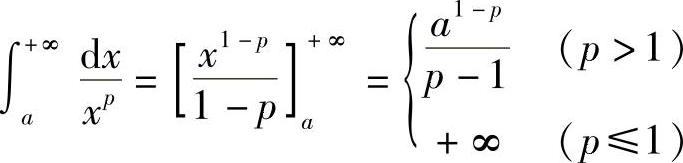
又因为当p=1时，.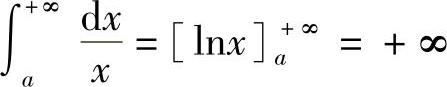

因此，当p＞1时，广义积分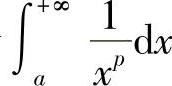收敛于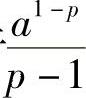，当p≤1时，此广义积分发散.二、无界函数的广义积分

若x₀是函数f（x）的无穷间断点，即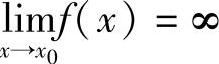，则x₀是f（x）的瑕点.

定义5.6 设函数f（x）在区间（a，b]上连续，且a为瑕点，取η＞0，如果极限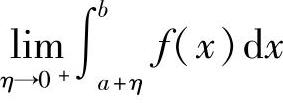存在，则称此极限值为无界函数f（x）在[a，b]上的广义积分或瑕积分，记作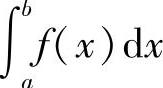，即

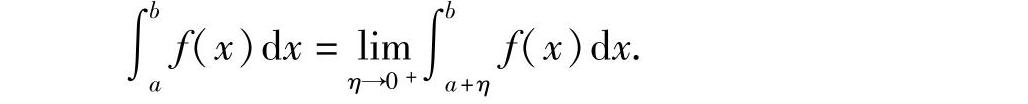
这时也称广义积分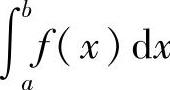收敛；若上述极限不存在，则称广义积分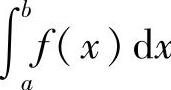发散.

当b为瑕点或c∈（a，b）为瑕点时，可类似地定义f（x）在[a，b]上的瑕积分

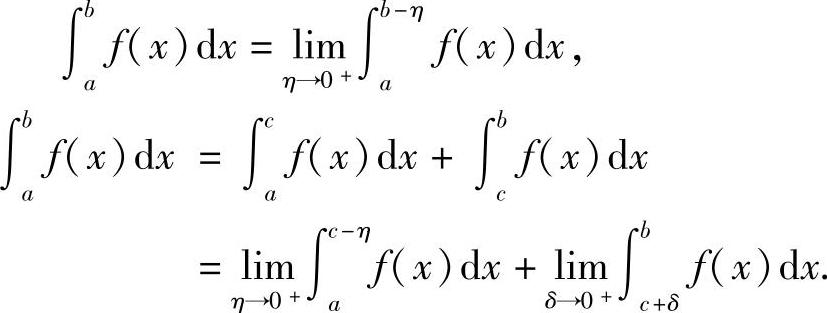
例4 计算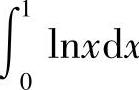.(https://www.daowen.com)

解 因为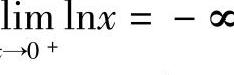，所以点x=0是瑕点，

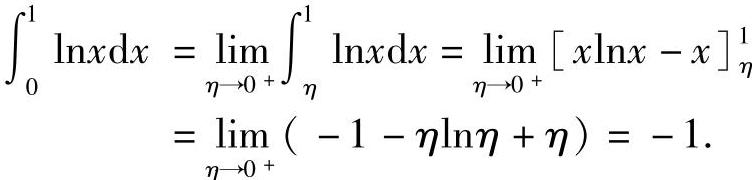
例5 讨论广义积分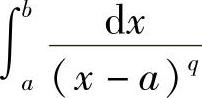的敛散性（b＞a＞0，q＞0）.

解 显然点x=a是瑕点，当q≠1时，

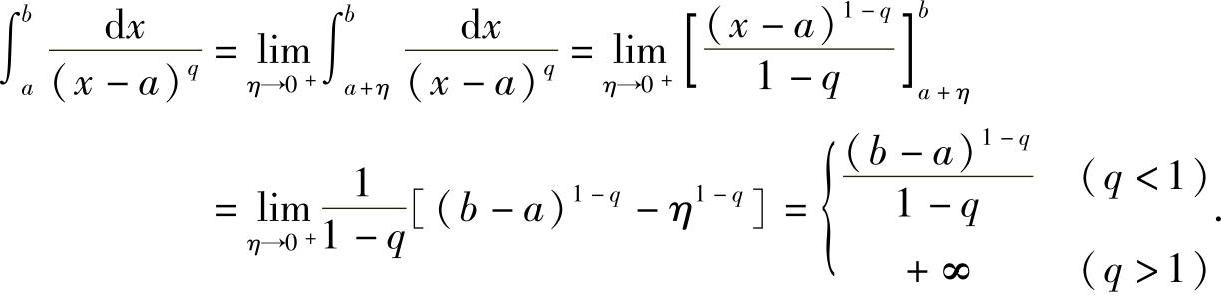
当q=1时，

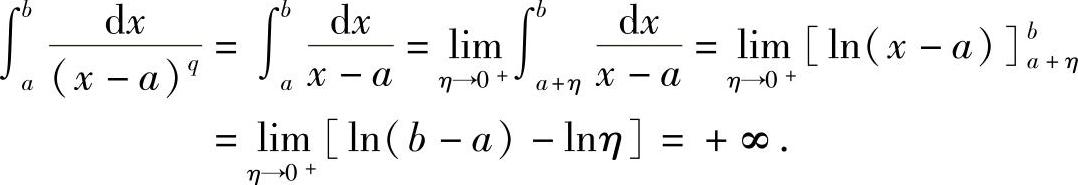
因此，广义积分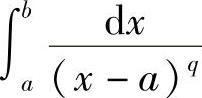，当q＜1时收敛；当q≥1时发散；同样可得，广义积分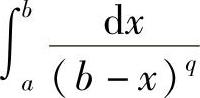，当q＜1时收敛，当q≥1时发散.三、Γ函数

定义5.7 积分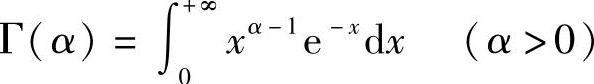称为Γ函数.

Γ函数有一个重要性质，即递推公式

Γ（α+1）=αΓ（α）.

这是因为

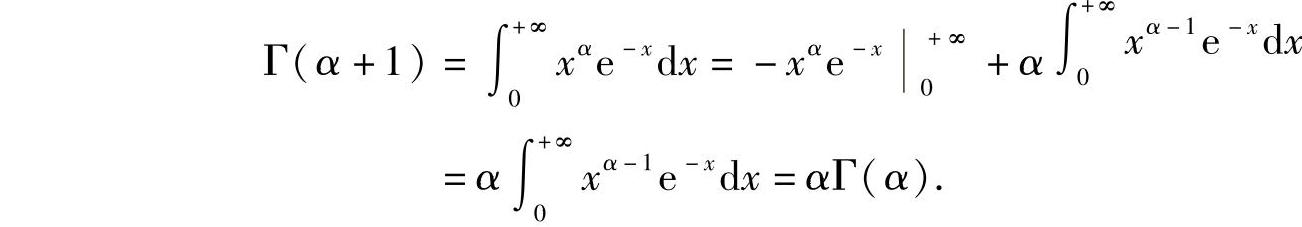
特别地

Γ（n+1）=n！

这是因为

Γ（n+1）=nΓ（n）=n（n-1）Γ（n-1）=…=n！Γ（1），又因为

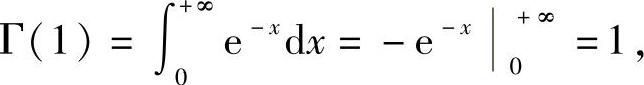
所以

Γ（n+1）=n！

Γ函数还可以写成另一种形式

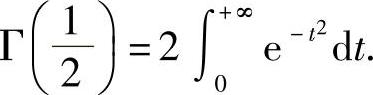
可以证明

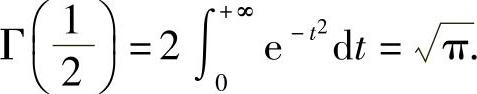
例6 计算.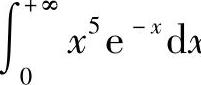

解 .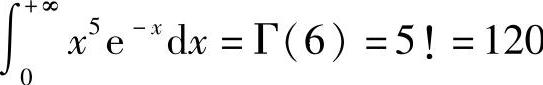

例7 计算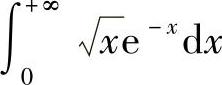

解 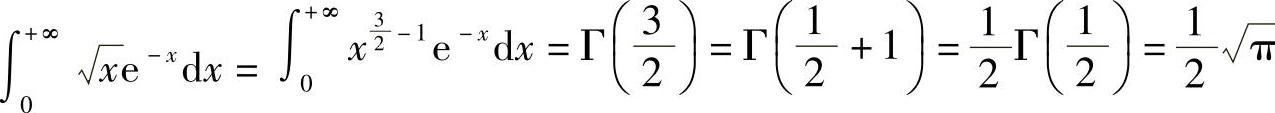.