第四节 微分
一、微分的概念
1.引例
一块正方形金属薄片受温度变化的影响,边长由x0变到x0+Δx,此薄片面积改变了多少?
如图2-3所示,设薄片边长为x,面积为A,则A=x2,当x在x0取得增量Δx时,面积的增量ΔA=(x0+Δx)2-x02=2x0Δx+(Δx)2.
ΔA包括两部分,第一部分2x0Δx是Δx的线性函数,第二部分(Δx)2为Δx的高阶无穷小.因此,当Δx很小时,就可以用2x0Δx来近似代替ΔA.用微分dA来表示,记作dA=2x0Δx.

图2-3
2.微分
定义2.3 设函数y=f(x)在x0的某个邻域内有定义,若函数y=f(x)在x0的改变量Δy与自变量x的改变量Δx满足
Δy=AΔx+ο(Δx)其中,A是与Δx无关的常数,则称函数y=f(x)在点x0处可微,AΔx称为函数f(x)在点x0处的微分,表示为dy=AΔx或df(x0)=AΔx.
dy通常也称为Δy的线性主部.
二、可微与可导的关系
定理2.6 函数y=f(x)在x0可微的充分必要条件是函数y=f(x)在x0可导,且A=f′(x0).即
dy=f′(x0)Δx.
证 先证必要性.
设函数f(x)在x0可微,即Δy=AΔx+ο(Δx),其中,A是与Δx无关的常数,两边同除以Δx,得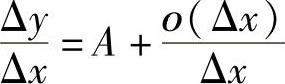 ,有
,有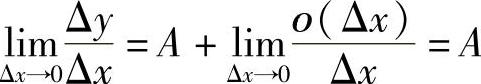 ,
,
所以函数y=f(x)在x0可导,且A=f′(x0).
再证充分性.
设函数y=f(x)在x0可导,即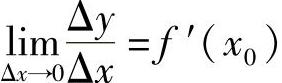
则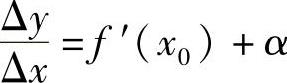 ,α→0(当Δx→0时).
,α→0(当Δx→0时).
从而Δy=f′(x0)Δx+αΔx=f′(x0)Δx+ο(Δx),其中,f′(x0)是与Δx无关的常数,ο(Δx)是比Δx高阶的无穷小,于是函数f(x)在x0可微,且A=f′(x0).
若对于函数y=x求微分,可得
dy=dx=(x)′·Δx=Δx.
于是函数f(x)在点x处的微分又可写作dy=f′(x)dx或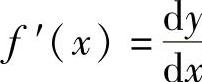 .在这个意义下,导数又叫做微商.
.在这个意义下,导数又叫做微商.
三、几何意义
如图2-4所示,PM是曲线y=f(x)在点P(x0,f(x0))处的切线.已知切线PM的斜率tanφ=f′(x0).
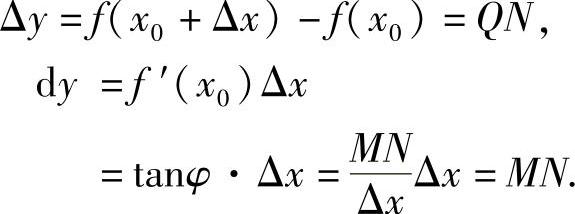 (https://www.daowen.com)
(https://www.daowen.com)
由此可见,dy=MN是曲线y=f(x)在点P(x0,y0)的切线PM的纵坐标的增量.因此,用dy近似代替Δy,就是用在点P(x0,y0)处切线的纵坐标的增量MN近似代替函数f(x)的增量QN,QM=QN-MN=Δy-dy=ο(Δx).
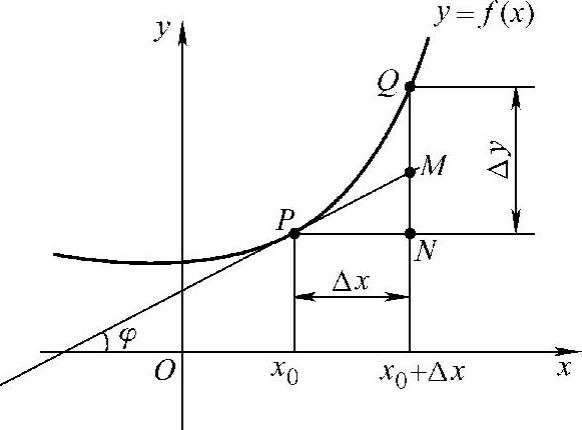
图2-4
四、微分法则
由dy=f′(x)dx,求微分dy,只要求出导数f′(x),再乘以dx即可.由导数公式和运算法则可相应地得到微分公式和微分运算法则:
1)dc=0 2)d(xμ)=μxμ-1dx;3)d(sinx)=cosxdx;4)d(cosx)=-sinxdx;5)d(tanx)=sec2xdx;6)d(cotx)=-csc2xdx;7)d(secx)=secx·tanxdx;8)d(cscx)=-cscx·cotxdx;9)d(ax)=axlnadx;10)d(ex)=exdx;11)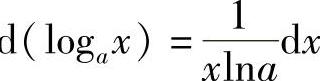 ;12)
;12)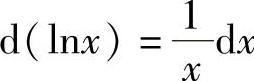 ;13)
;13)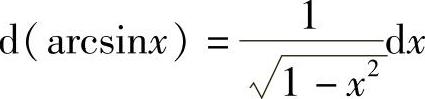 ;14)
;14)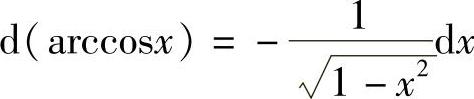 ;15)
;15)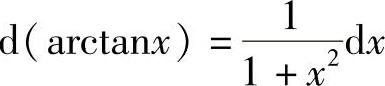 ;16)
;16)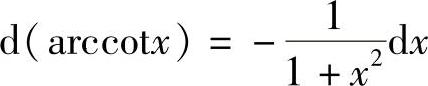 ;17)d(u±v)=du±dv;18)d(uv)=vdu+udv;19)
;17)d(u±v)=du±dv;18)d(uv)=vdu+udv;19)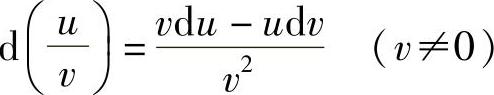 .
.
五、微分形式不变性
设y=f(u),u=φ(x),则复合函数y=f(φ(x))的微分为
dy=yx′dx=f′(u)φ′(x)dx.
由于φ′(x)dx=du,所以复合函数y=f(φ(x))的微分公式也可以写成
dy=f′(u)du或dy=yu′du.
由此可见,无论u是自变量还是自变量的可导函数,微分形式dy=f′(u)du保持不变,这一性质称为微分形式不变性.
例1 求y=exsinx的微分.
解 方法一:利用微分公式dy=f′(x)dx,得
dy=(exsinx)′dx=ex(sinx+cosx)dx.
方法二:利用微分形式不变性,得
dy=sinxdex+exdsinx=ex(sinx+cosx)dx.
六、微分在近似计算中的应用
若函数y=f(x)在x0可微,则Δy=dy+ο(Δx),即
f(x0+Δx)-f(x0)=f′(x0)Δx+ο(Δx).当|Δx|→0时,忽略高阶无穷小量,得
f(x)≈f(x0)+f′(x0)Δx.
例2 求tan31°的近似值.
解 设f(x)=tanx,
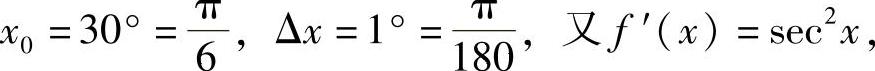
有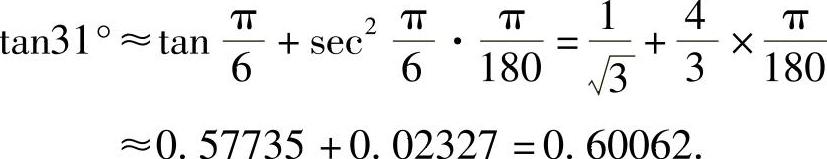
例3 求e-0.01的近似值.
解 设f(x)=ex,x0=0,Δx=-0.01,又f′(x)=ex,有e-0.01≈e0+e0(-0.01)=0.99.
