定积分的概念和性质
一、引例
1.曲边梯形的面积
设函数y=f(x)在闭区间[a,b]上非负且连续,则曲线y=f(x)与直线x=a,x=b,y=0围成的图形(见图5-1)称为曲边梯形.求其面积A的基本思想是在很小的区间上用小矩形面积近似代替小梯形面积.
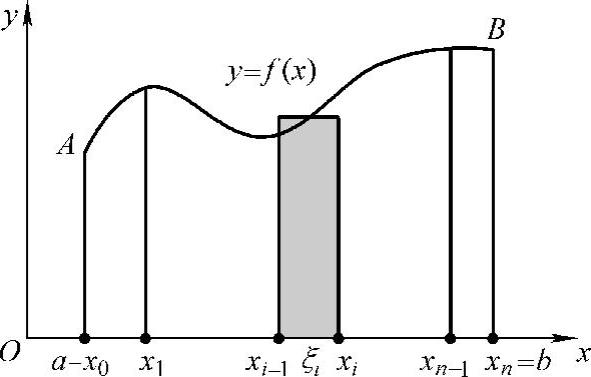
图5-1
第一步:分割.
用一串分点a=x0<x1<…<xn=b,把[a,b]分成n个小区间,过每个分点作x轴的垂线段,相应地把曲边梯形分成n个小曲边梯形,其中,第i个小曲边梯形为
xi-1≤x≤xi,0≤y≤f(x),记它们的面积依次为
ΔA1,ΔA2,…,ΔAn.
第二步:取近似.
在每个小区间[xi-1,xi]上任取一点ξi,以区间[xi-1,xi]的长为底,f(ξi)为高的小矩形的面积应为第i个小曲边梯形面积的近似值,即
ΔAi≈f(ξi)Δxi.
第三步:作和.
将n个小矩形的面积相加,得到曲边梯形面积A的近似值,即
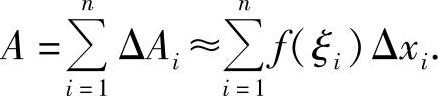
第四步:求极限(由近似过渡到精确).
显然上述过程划分得越细,近似效果越好,为保证每个小区间的长度都无限小,记
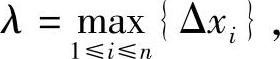
于是,令λ→0(这时小区间的个数n无限增多,即n→∞),如果上述和式极限存在,则此极限值就是曲边梯形的面积,即
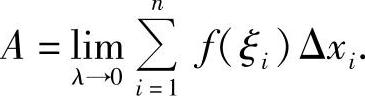
2.变速直线运动的路程问题
设物体作变速直线运动,其速度v是时间t的函数v=v(t),下面计算该物体从时刻a到时刻b经过的路程s.
第一步:分割.
用一串分点a=t0<t1<…<tn=b,把[a,b]分成n个小区间[tj-1,tj],小区间长度记为Δtj=tj-tj-1(j=1,2,…,n),各时间段内物体运动的路程依次为
Δs1,Δs2,…,Δsn.
第二步:取近似.
在[tj-1,tj]上任取一点τj,以时刻τj的速度v(τj)近似代替[tj-1,tj]上的速度,则在Δtj时间内物体经过的路程Δsj的近似值为
Δsj≈v(τj)Δtj.
第三步:作和.
将n个时间段的路程近似值相加,便得到总路程s的近似值:
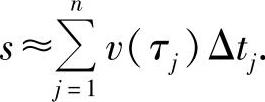
第四步:求极限.
记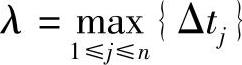 ,令λ→0,如果上述和式极限存在,则此极限值就是总路程s
,令λ→0,如果上述和式极限存在,则此极限值就是总路程s
的精确值,
即
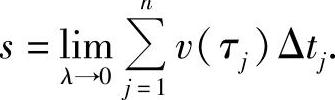
二、定积分的定义
上面的两个例子,前者是几何量,后者为物理量,虽然问题不同但解决的方法是相同的,都是通过“分割、近似、作和、求极限”这四个步骤化为具有同一数学结构的和式极限.抛开问题的实际意义,保留其数学结构,便可抽象出定积分的概念.
定义5.1 设f(x)在区间[a,b]有定义,在[a,b]内任意插入n-1个分点:a=x0<x1<x2<…<xn-1<xn=b,将[a,b]分成n个小区间:[x0,x1],[x1,x2],…,[xi-1,xi],…,[xn-1,xn],第i个小区间[xi-1,xi]的长度表示为Δxi=xi-xi-1,记λ1=≤im≤nax{Δxi}在[xi-1,xi]中任取一点ξi(i=1,2,3,…,n),作和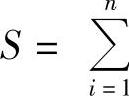 f(ξi)Δxi.如果当λ→0时,S趋于确定的极限I,且I与分法无关,也与ξi在[xi-1,xi]中的取法无关,则称f(x)在[a,b]上可积,极限I称为f(x)在[a,b]上的定积分,记作∫baf(x)dx,即
f(ξi)Δxi.如果当λ→0时,S趋于确定的极限I,且I与分法无关,也与ξi在[xi-1,xi]中的取法无关,则称f(x)在[a,b]上可积,极限I称为f(x)在[a,b]上的定积分,记作∫baf(x)dx,即
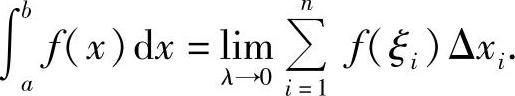
其中,f(x)叫做被积函数,f(x)dx叫做被积表达式,x叫做积分变量,a与b叫做积分下限与积分上限.
如果当λ→0时,积分和S不存在极限,则称f(x)在[a,b]上不可积.
注:1)定积分的值只与被积函数f(x)以及积分区间[a,b]有关,而与积分变量用什么字母表示无关,即
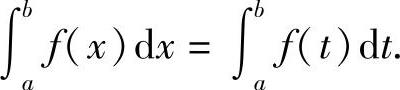
2)被积函数f(x)在区间[a,b]上有界只是可积的必要条件,关于可积的充分条件只给出如下三个结论,而不作深入研究.
定理5.1 若函数f(x)在区间[a,b]上连续,则f(x)在区间[a,b]上可积.
定理5.2 若函数f(x)在区间[a,b]上有界,且只有有限个间断点,则f(x)在区间[a,b]上可积.
定理5.3 若函数f(x)在区间[a,b]上是单调的,则f(x)在区间[a,b]上可积.
3)为计算和使用方便,作如下规定:
规定1 当a=b时,∫baf(x)dx=∫aaf(x)dx=0;
规定2 当a>b时,∫baf(x)dx=-∫abf(x)dx.
4)根据定积分的定义,前面两个引例中,曲边梯形的面积A用定积分可表示为
A=∫baf(x)dx.变速直线运动的路程s用定积分可表示为
s=∫bav(x)dx.三、定积分的几何意义
若在[a,b]上,f(x)≥0,则定积分∫baf(x)dx表示由曲线y=f(x),x轴及直线x=a,x=b所围成的曲边梯形的面积.
若f(x)≤0,则定积分∫baf(x)dx表示上述曲边梯形的面积的相反数.
若函数f(x)在[a,b]上有正有负,则定积分∫baf(x)dx表示各部分面积的代数和.如图5-2所示.
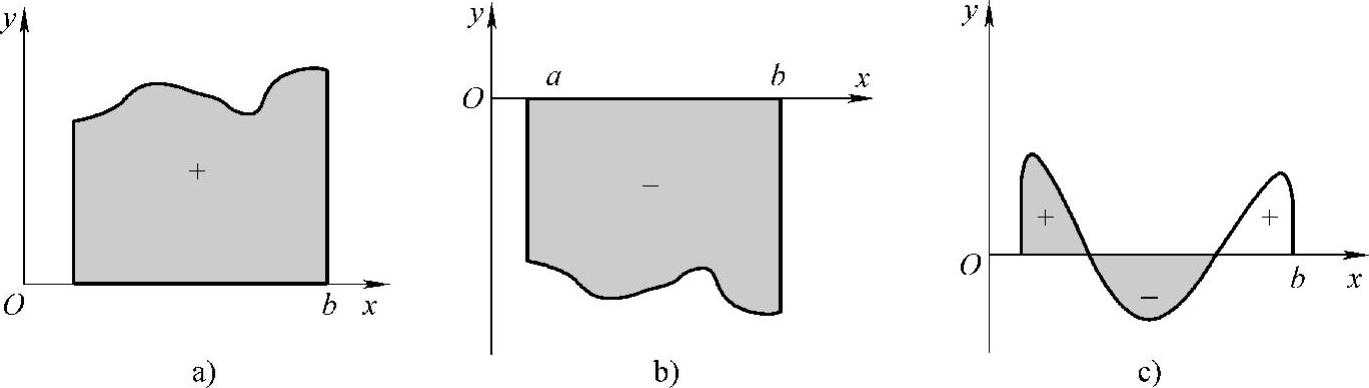
图5-2
例1 计算定积分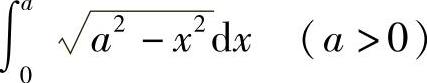 .
.
解 由定积分的几何意义知,该积分值等于由x=0,x=a,y=0和y=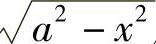 所围半径为a的四分之一圆的面积,(https://www.daowen.com)
所围半径为a的四分之一圆的面积,(https://www.daowen.com)
即
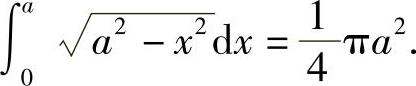
例2 计算定积分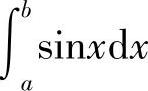
解 因为f(x)=sinx在[a,b]上连续,故sinx在[a,b]上可积,因此可以对[a,b]采用特殊的分法,以及选取特殊的点ξi,取极限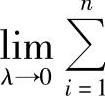 f(ξi)Δxi,即得到积分值.
f(ξi)Δxi,即得到积分值.
将[a,b]n等分,则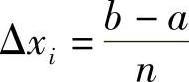 ,取
,取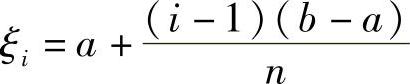 ,i=1,2,…,n则有
,i=1,2,…,n则有
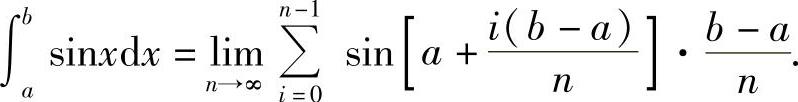
为了书写方便,令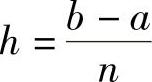 ,利用积化和差公式有
,利用积化和差公式有
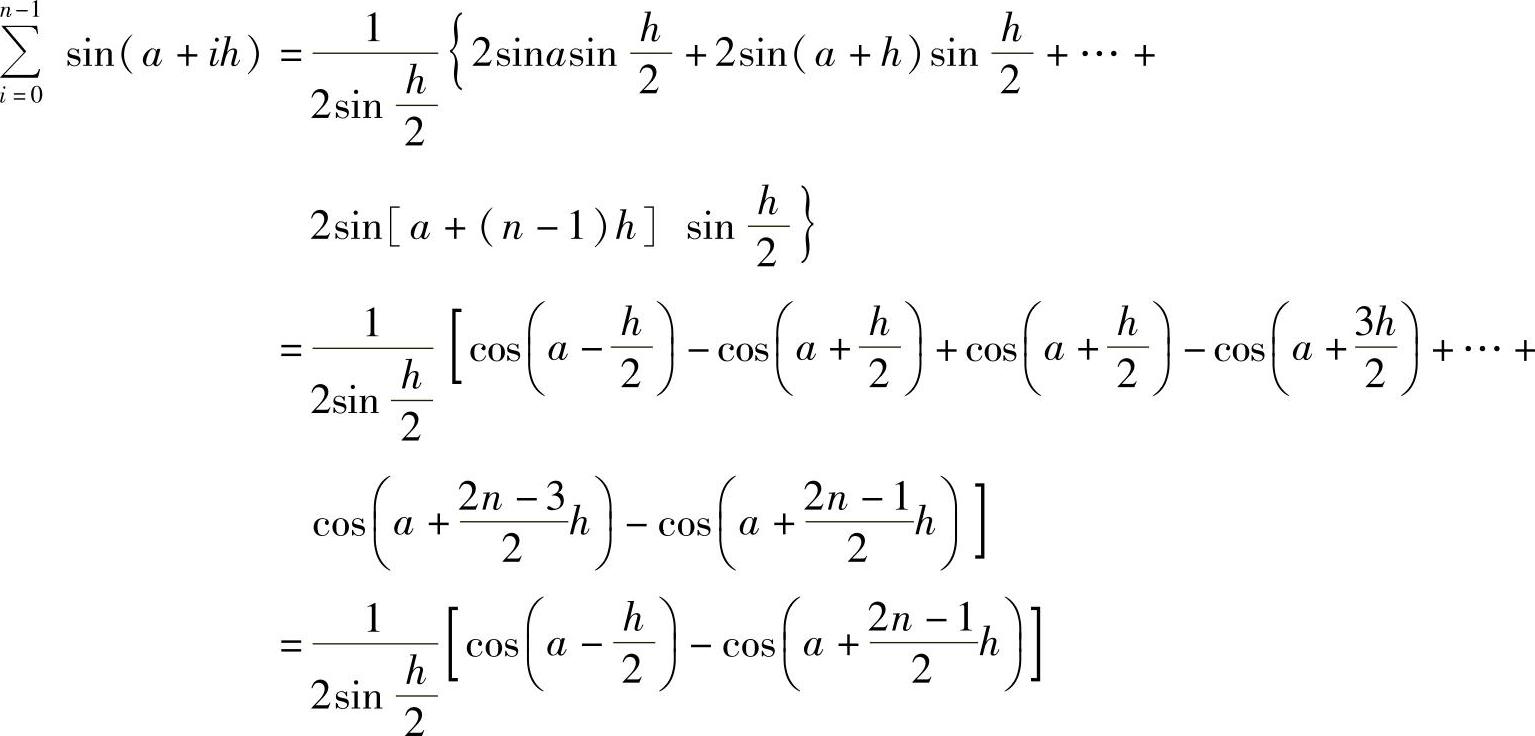
所以
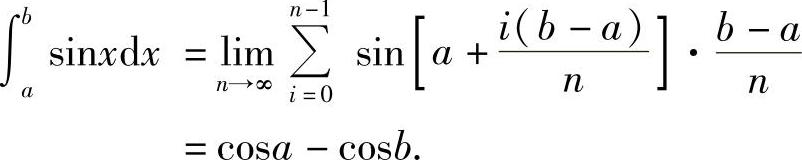
四、定积分的基本性质
在下面讨论中,总假设函数在所讨论的区间上都是可积的.
性质1 ∫ba[f(x)±g(x)]dx=∫baf(x)dx±∫bag(x)dx.
证 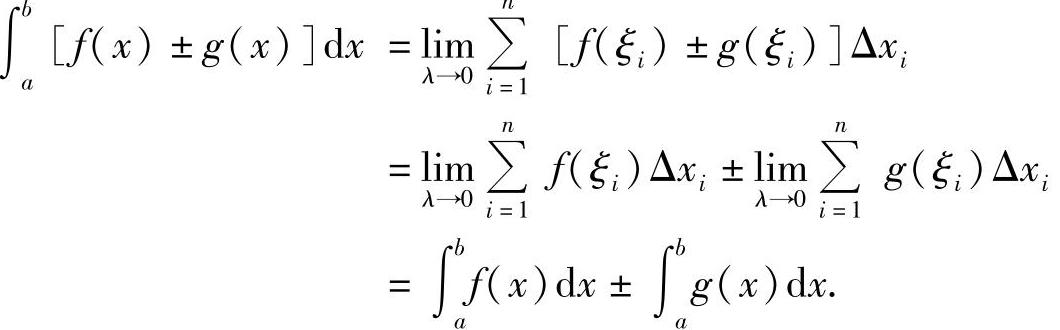
性质2 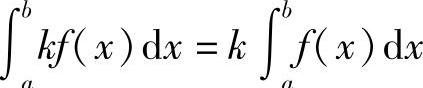 (k为常数).
(k为常数).
性质3(积分区间的可加性) 如果将积分区间分成两部分,则在整个区间上的定积分等于这两部分区间上定积分之和,设a<c<b,则
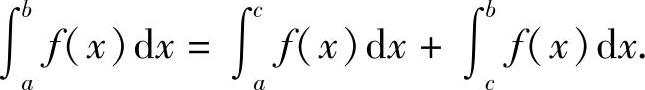
证 因为函数f(x)在[a,b]上可积,所以不论把[a,b]怎样划分,也不论ξi怎样选取,当λ→0时,积分和的极限都是不变的,所以可以选取c(a<c<b)永远是个分点
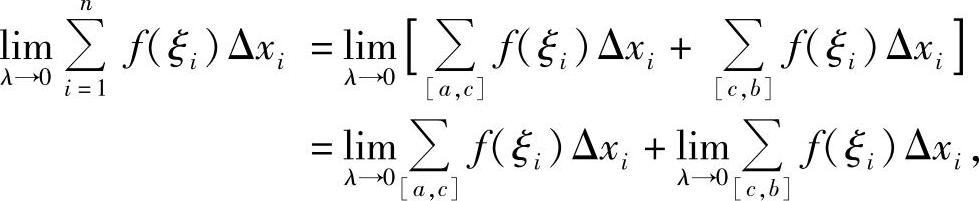
即
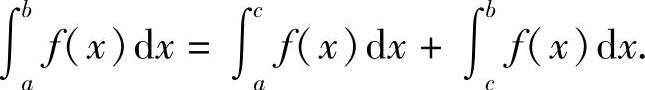
推广 不论a,b,c的相对位置如何,总有等式
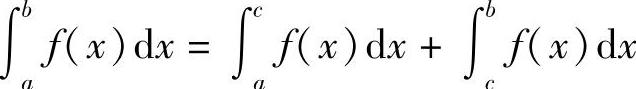
成立.例如,当a<b<c时,由于
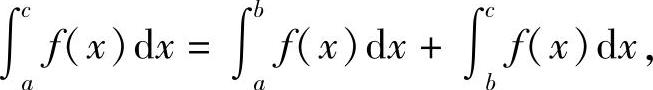
则
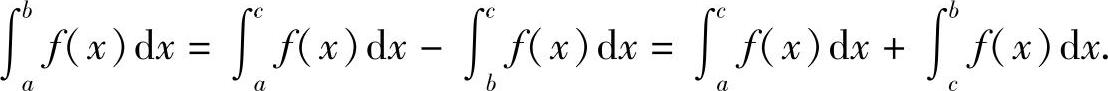
性质4 如果在闭区间[a,b]上f(x)≡1,则
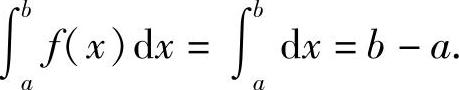
性质5 如果在闭区间[a,b]上f(x)≥0,则
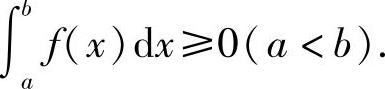
证 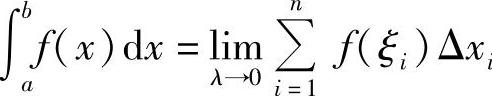 .
.
因为f(x)≥0,故f(ξi)≥0(i=1,2,…,n),又因为Δxi≥0(i=1,2,…,n),因此
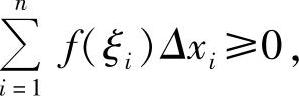
所以
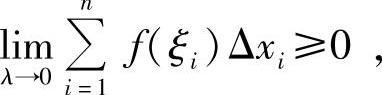
即
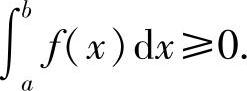
推论5.1 如果在闭区间[a,b]上,f(x)≤g(x),则
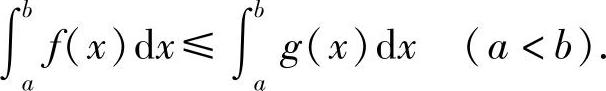
推论5.2 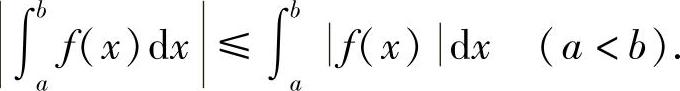
性质6 设M和m分别是函数f(x)在闭区间[a,b]上的最大值和最小值,则
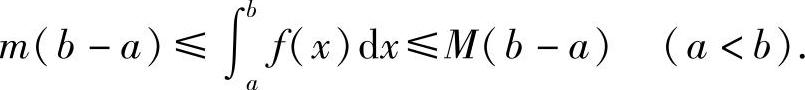
证 因为m≤f(x)≤M,由推论5.1得
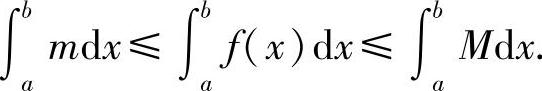
再由性质2及性质4可得
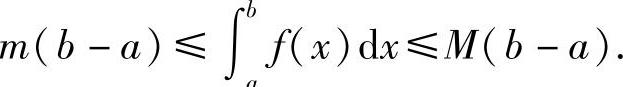
性质7 如果函数f(x)在闭区间[a,b]上连续,则在积分区间[a,b]上至少存在一点ξ,使下式成立
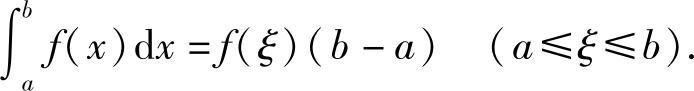
证 因f(x)在[a,b]上连续,故必存在最大值M与最小值m,由性质6,有
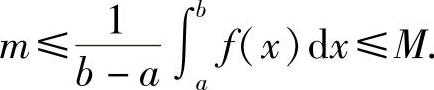
这说明,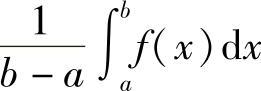 介于M与m之间,根据闭区间上连续函数的介值定理(第一章第七节定理1.22),在区间[a,b]内存在一点ξ,使得函数f(x)在点ξ处的值与这个值相等,
介于M与m之间,根据闭区间上连续函数的介值定理(第一章第七节定理1.22),在区间[a,b]内存在一点ξ,使得函数f(x)在点ξ处的值与这个值相等,
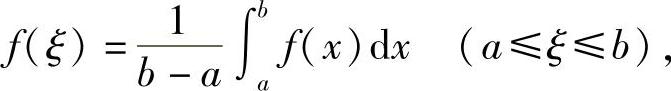
即
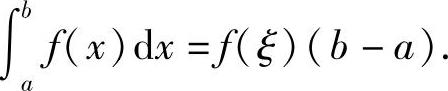
此性质称为积分中值定理
积分中值定理有其明显的几何意义:
设f(x)≥0,由曲线y=f(x),x轴及直线x=a,x=b所围成的曲边梯形的面积等于以区间[a,b]为底,某一函数值f(ξ)为高的矩形面积(见图5-3).
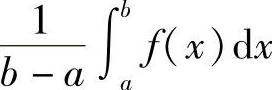
称为函数f(x)在区间[a,b]上的平均值.
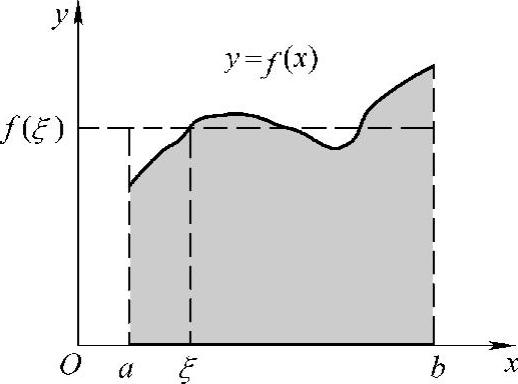
图5-3
