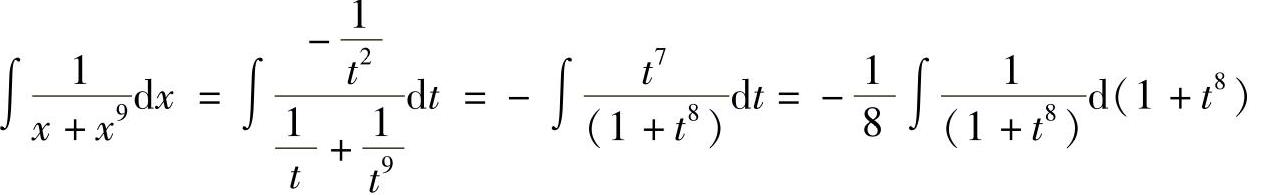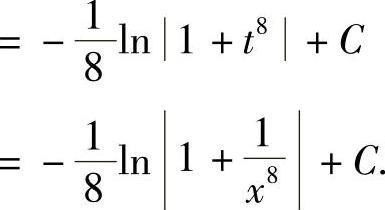换元积分法

第二节 换元积分法

一、第一类换元法

在上一节中，虽已介绍了一些求原函数的方法，但这些方法在有些情况下是不够的.例如，∫cos2xdx就不易求解.

如果令2x=u，可得

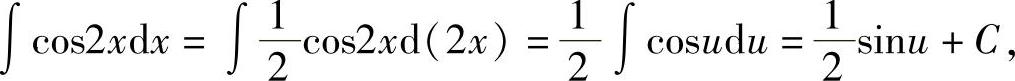
代回原变量，得.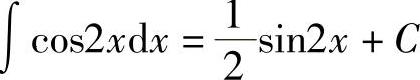

一般地，设f（u）是u的连续函数，且∫f（u）du=F（u）+C，若u=φ（x）有连续的导数φ′（x），则

∫f（φ（x））φ′（x）dx=F（φ（x））+C

要证明上式成立，只需证明[F（φ（x））]′=f（φ（x））φ′（x）即可.

因为[F（φ（x））]′=F′（φ（x））φ′（x），又由∫f（u）du=F（u）+C，得F′（u）=f（u），故[F（φ（x））]′=f（φ（x））φ′（x）成立.

上述通过换元求不定积分的方法称为第一类换元法.

例1 求.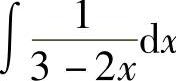

解 令u=3-2x，则du=-2dx，故

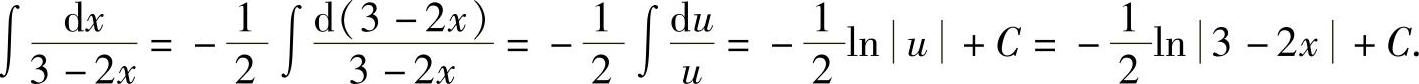
例2 求∫tanxdx.

解 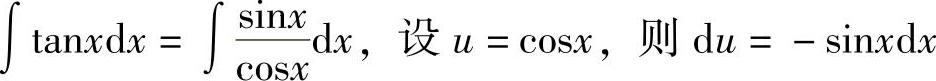，因此，.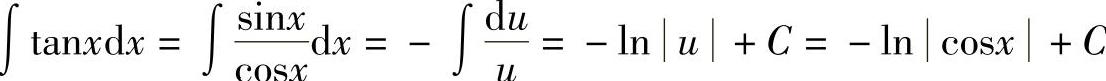

类似地，有∫cotxdx=ln sinx+C.

当运算熟练以后，可以不必写出u，而直接写出结果.

例3 求.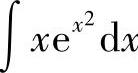

解 .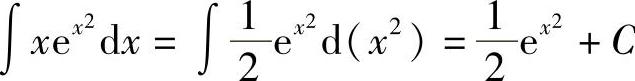

例4 求.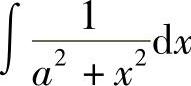

解 .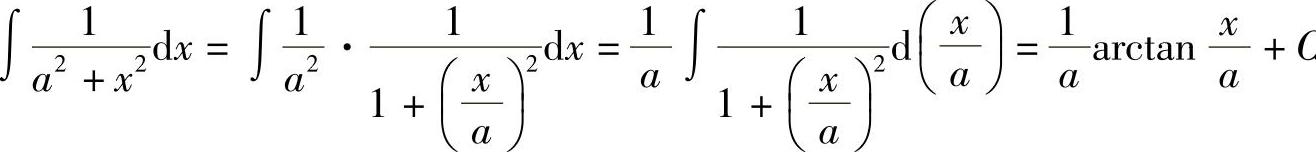

例5 求．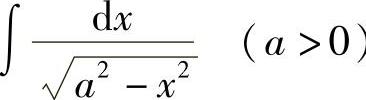

解 .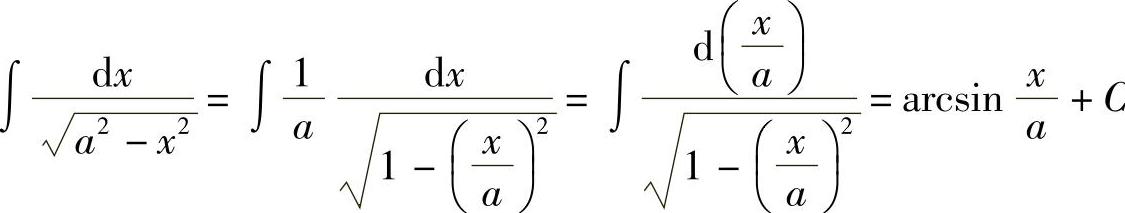

例6 求.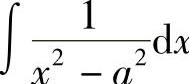

解 由于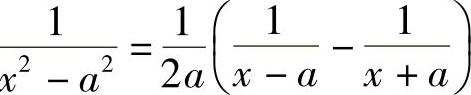，所以

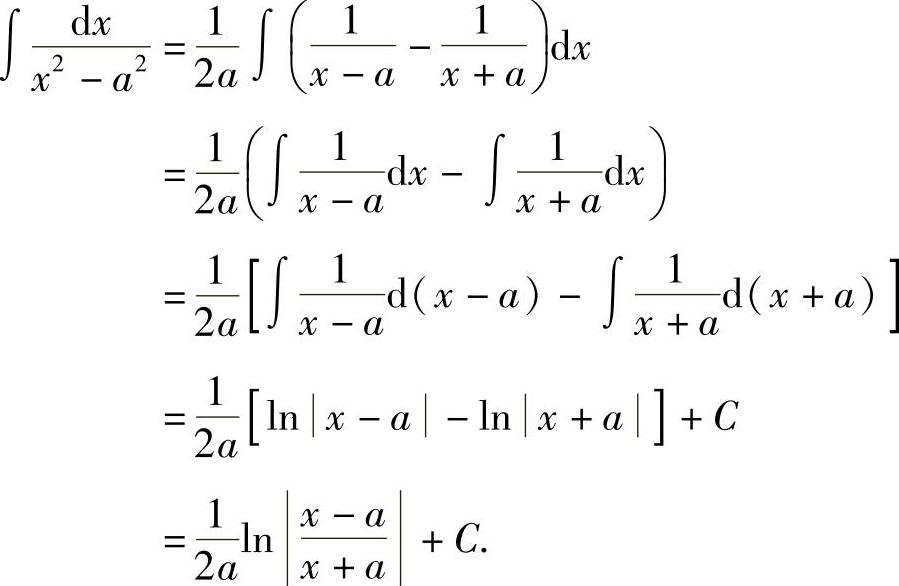
例7 求.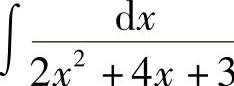

解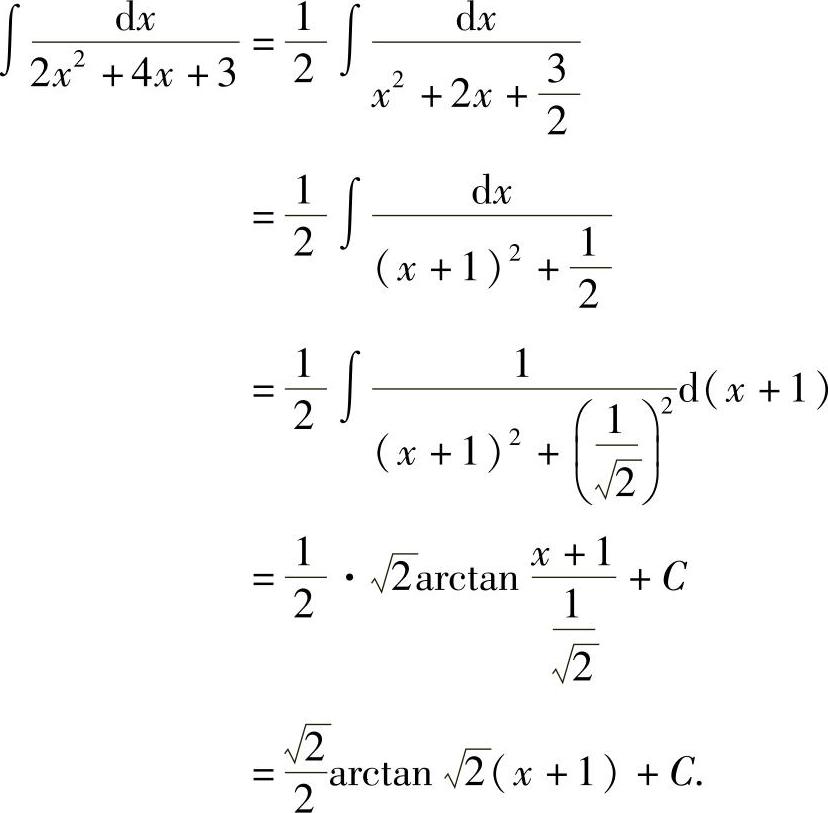

例8 求∫sin³xdx.

解 .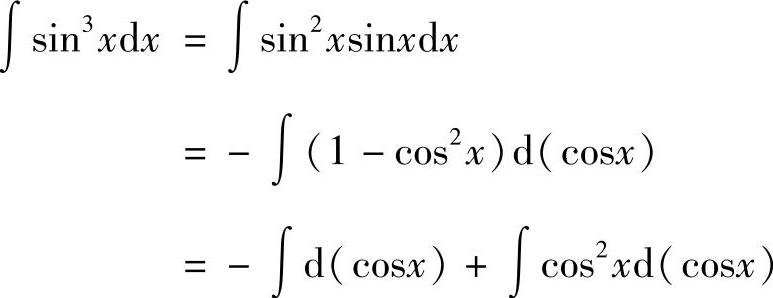

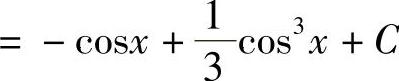例9 求∫cos²xdx.

解 ．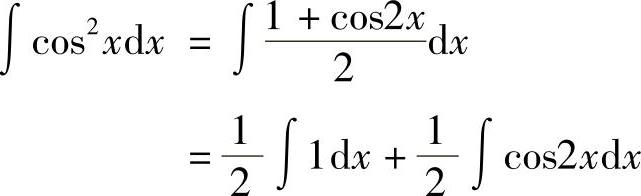

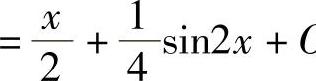类似地，有.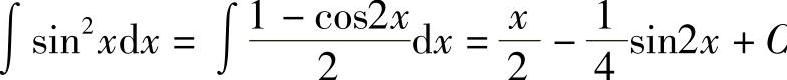

例10 求∫cscxdx.

解 .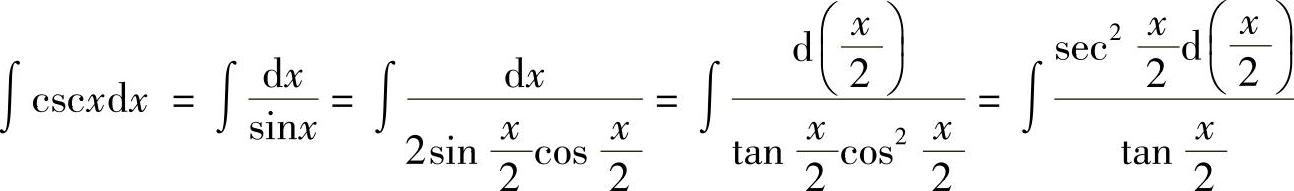

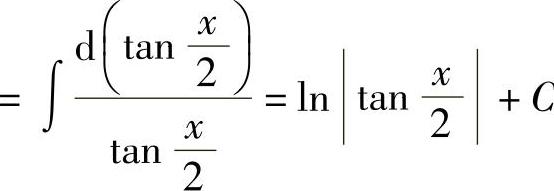又因为.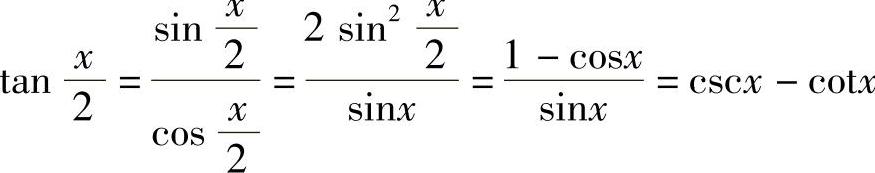

所以上述不定积分又可表示为

∫cscxdx=ln|cscx-cotx|+C.

类似地，有∫secxdx=ln|secx+tanx|+C.

例11 求∫sin2xcos3xdx.

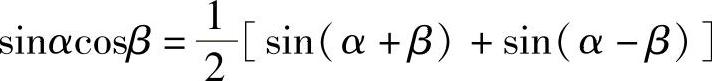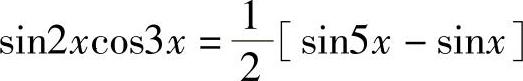解 利用积化和差公式，得，所以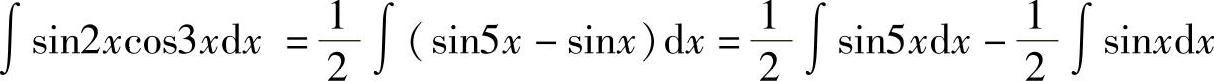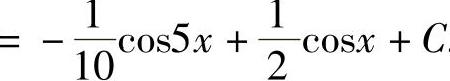.二、第二类换元法(https://www.daowen.com)

对于某些特殊的不定积分∫f（x）dx，可以引入新的变量t，将x表示为t的函数，从而简化积分计算.这种换元法称为第二类换元法.

设函数x=φ（t）严格单调、可导，且φ′（t）≠0，又设f（φ（t））φ′（t）具有原函数.

则有换元公式

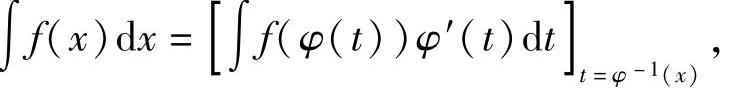
其中，φ^-1（x）是x=φ（t）的反函数.

证 设∫f（φ（t））φ′（t）dt=F（t）+C，要证明上式成立，只需证[F（φ^-1（x））+C]′=f（x）.

而.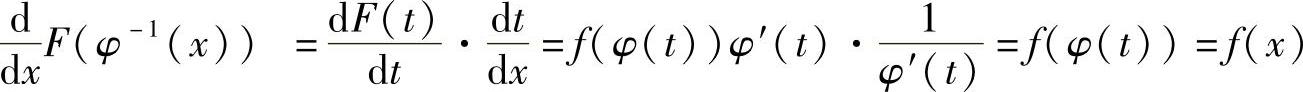

例12 求.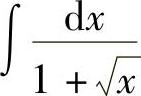

解 作变量代换x=t，于是x=t²，dx=2tdt，从而

.

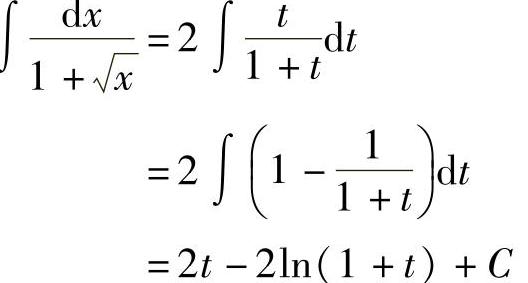
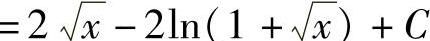例13 求.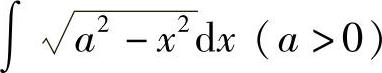

解 令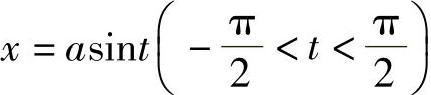，则，，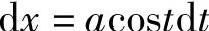

，

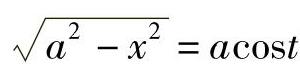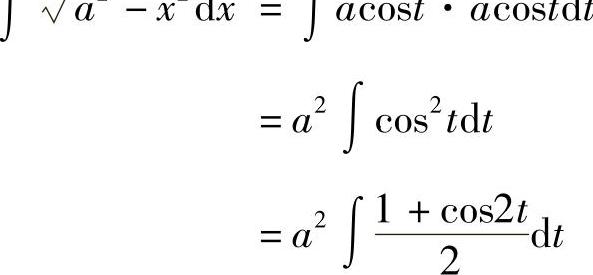
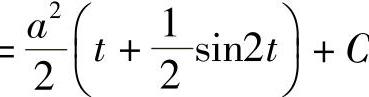由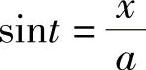作辅助三角形（见图4-3），得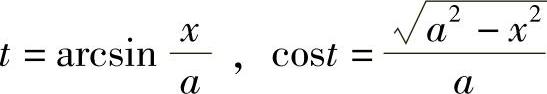，故．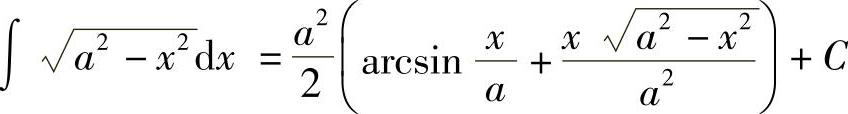

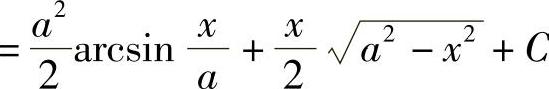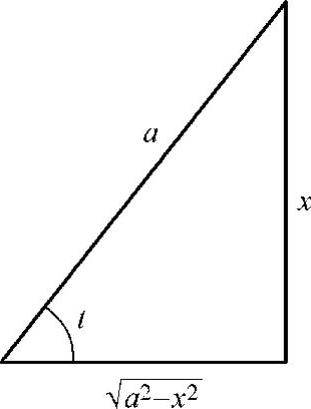
图4-3

例14 求.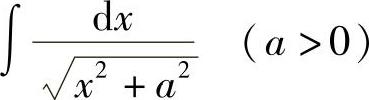

解 设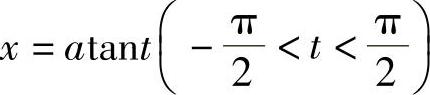，则dx=asec²tdt，

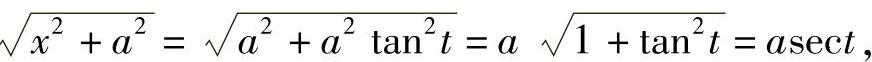
从而.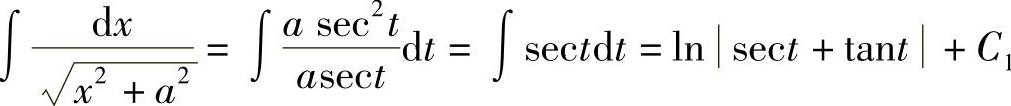

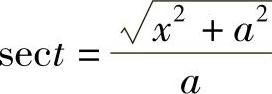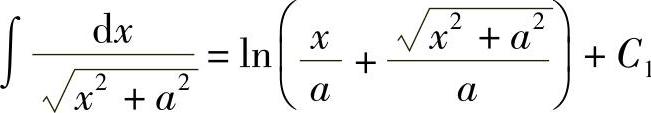
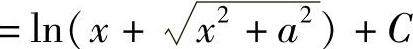由tant=x作辅助三角形（见图4-4），得，故，其中，C=C₁-lna.

例15 求.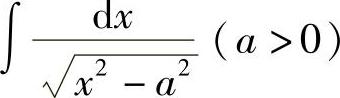

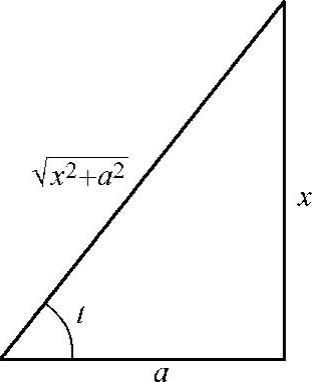
图4-4

解 当x＞a时，令x=asect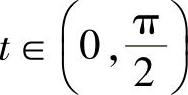，，则，dx=asecttantdt，从而．

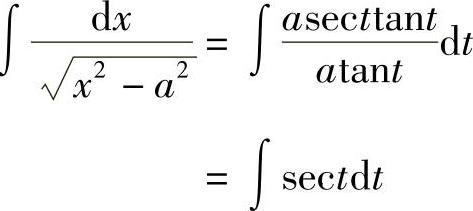
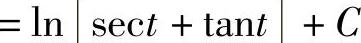由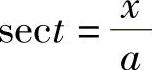作辅助三角形（见图4-5），得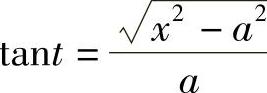，故

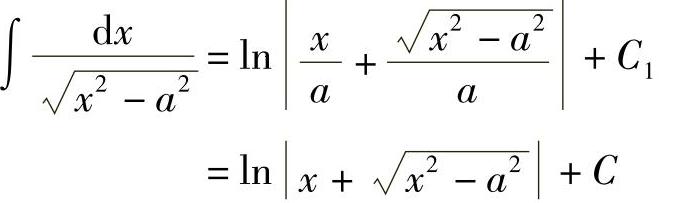
其中，C=C₁-lna.

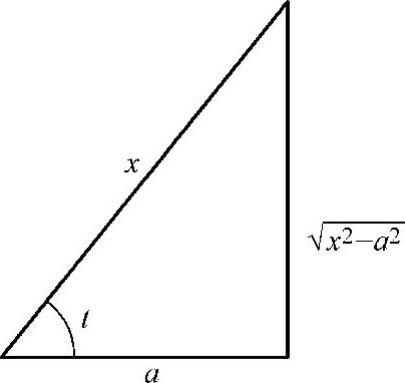
图4-5

当x＜-a时，令x=-u，则u＞a，从而

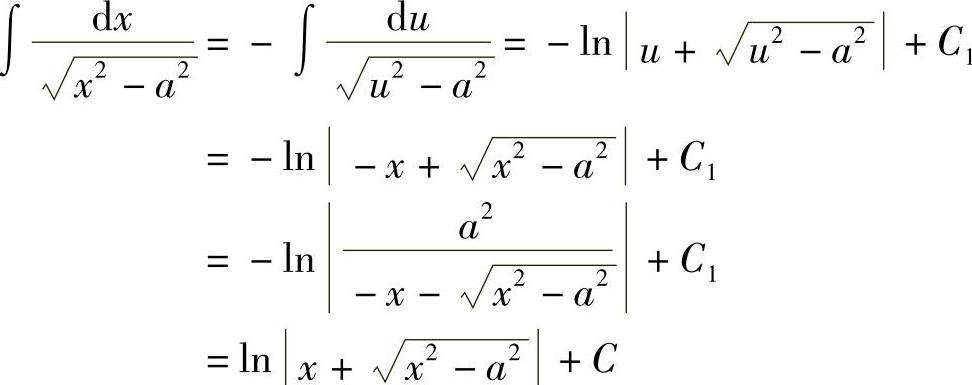
其中，C=C₁-2lna.

综上所述，.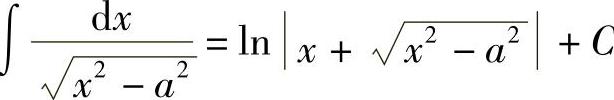

例16 求.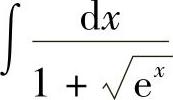

解 ．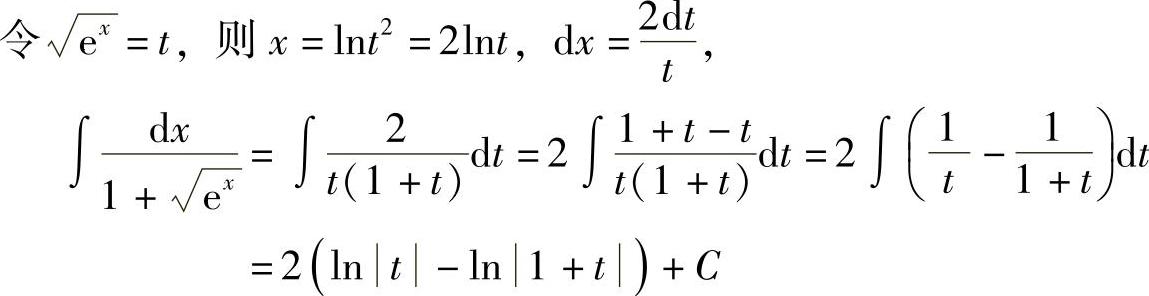

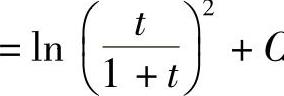将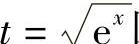回代.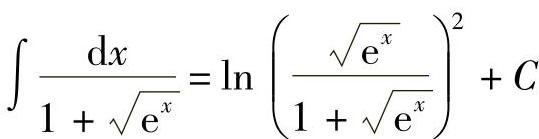

例17 求.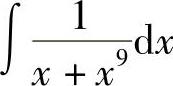

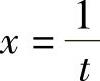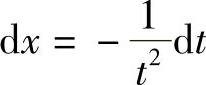解 令，则，故