习题3.1

1.验证函数f（x）=x²-2x-3在闭区间[-1，3]上满足罗尔定理，并求出定理中的ξ.

2.验证函数f（x）=arctanx在区间[0，1]上满足拉格朗日中值定理，并求出定理中的ξ.

3.证明不等式sinx₂-sinx₁≤x₂-x₁.

4.设a＞b＞0，证明不等式.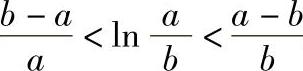

5.设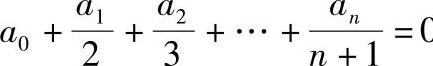0，证明多项式f（x）=a₀+a₁x+a₂x²+…a_nxⁿ在（0，1）内至少有一个零点.

6.若函数f（x）在（a，b）内具有二阶导数，且f（x₁）=f（x₂）=f（x₃），其中，a＜x₁＜x₂＜x₃<b，证明：在（x₁，x₃）内至少存在一点ξ，使得f″（ξ）=0.

7.证明：.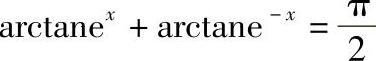

8.证明多项式f（x）=x³-3x+a在[0，1]上不可能有两个零点.

9.设b＞a＞0，函数f（x）在[a，b]上连续，在（a，b）内可导，利用柯西中值定理，证明至少存在一点ξ∈（a，b），使得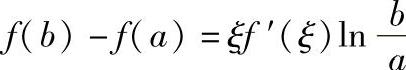.