不定积分的概念与性质
一、原函数与不定积分
定义4.1 设f(x)是定义在区间I上的函数,如果存在函数F(x),对于任意x∈I,都有
F′(x)=f(x)或dF(x)=f(x)dx
则称函数F(x)为函数f(x)在区间I上的一个原函数.
例如,因为(sinx)′=cosx,则sinx是cosx的原函数.
又因为(sinx+1)′=cosx,所以sinx+1也是cosx的原函数.
由此例可以看出,一个函数若有原函数,则原函数可以不止一个.
实际上,若函数F(x)为函数f(x)的一个原函数,即F′(x)=f(x),则(F(x)+C)′=f(x)(其中,C为任意常数),所以F(x)+C都是f(x)的原函数.
所以,函数f(x)的原函数有无穷多个.
另一方面,如果F(x),G(x)为函数f(x)在区间I上的任意两个原函数,即[F(x)]′=f(x),[G(x)]′=f(x),则[G(x)-F(x)]′=G′(x)-F′(x)=f(x)-f(x)=0所以G(x)-F(x)=C,即G(x)=F(x)+C.
所以,函数f(x)的任意两个原函数仅相差一个常数.
定义4.2 函数f(x)的所有原函数称为f(x)的不定积分,记作∫f(x)dx.其中,∫称为积分号,f(x)称为被积函数,f(x)dx称为被积表达式,x称为积分变量.
因此,若F(x)是f(x)的一个原函数,那么∫f(x)dx=F(x)+C.
例1 求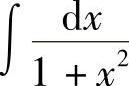 .
.
解 由于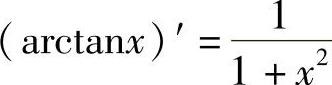 ,所以arctanx是
,所以arctanx是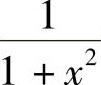 的一个原函数,因此
的一个原函数,因此
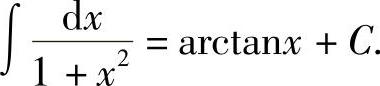
例2 求函数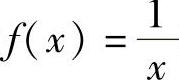 的不定积分.
的不定积分.
解 当x>0时,由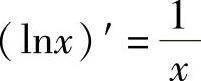 ,得
,得
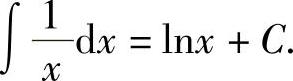
当x<0时,由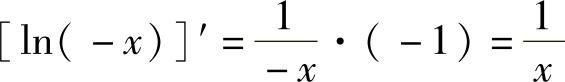 ,得
,得
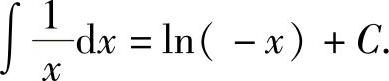
综合两种情况,可得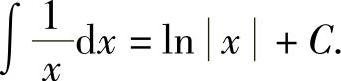
二、不定积分的性质
由于求不定积分是求导数或微分的逆运算,故有如下性质:
[∫f(x)dx]′=f(x)或d[∫f(x)dx]=f(x)dx;∫F′(x)dx=F(x)+C或∫dF(x)=F(x)+C.
由导数运算的线性性质,还可以得到如下性质:
1)∫[f(x)+g(x)]dx=∫f(x)dx+∫g(x)dx;2)∫kf(x)dx=k∫f(x)dx(k为常数,k≠0).
证 1)[∫f(x)dx+∫g(x)dx]′=[∫f(x)dx]′+[∫g(x)dx]′=f(x)+g(x).(https://www.daowen.com)
推广之,有限个函数的和也有这一性质.
2)类似可证.
此外,至于函数f(x)在什么条件下才有原函数,将在下一章给出说明,先给出结论:
若函数f(x)在某一区间上连续,则在此区间上f(x)的原函数一定存在.
三、基本积分公式
因为求不定积分是求导数的逆运算,则由基本导数公式对应地可以得到基本积分公式:
1)∫kdx=kx+C(k是常数);2)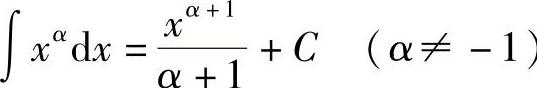 );3)
);3)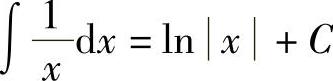 ;4)
;4)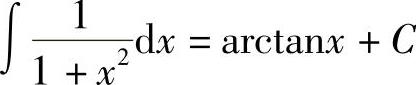 ;5)
;5)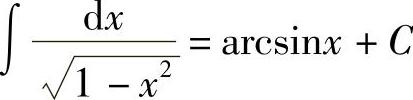 ;6)∫exdx=ex+C;7)
;6)∫exdx=ex+C;7)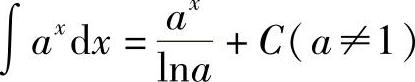 ;8)∫cosxdx=sinx+C;9)∫sinxdx=-cosx+C;10)∫sec2xdx=tanx+C;11)∫csc2xdx=-cotx+C;12)∫secxtanxdx=secx+C;13)∫cscxcotxdx=-cscx+C.
;8)∫cosxdx=sinx+C;9)∫sinxdx=-cosx+C;10)∫sec2xdx=tanx+C;11)∫csc2xdx=-cotx+C;12)∫secxtanxdx=secx+C;13)∫cscxcotxdx=-cscx+C.
例3 求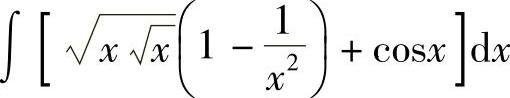 .
.
解 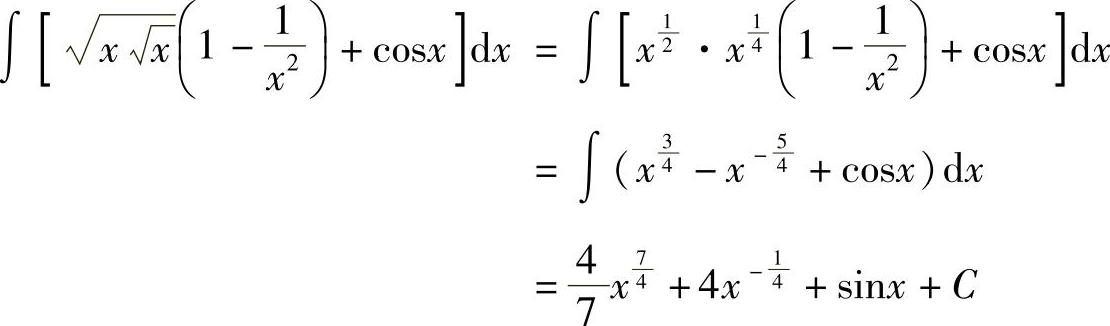
例4 求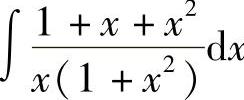 .
.
解 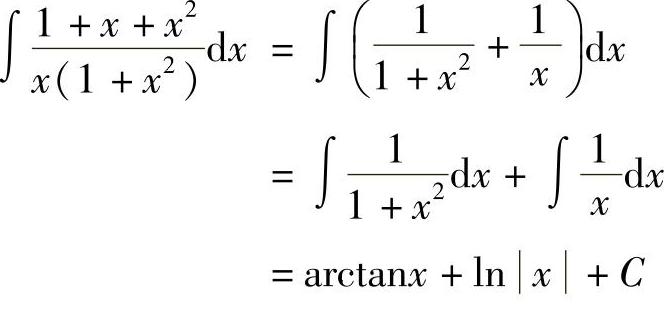
例5 求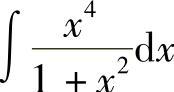 .
.
解 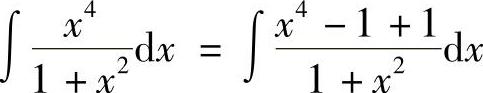
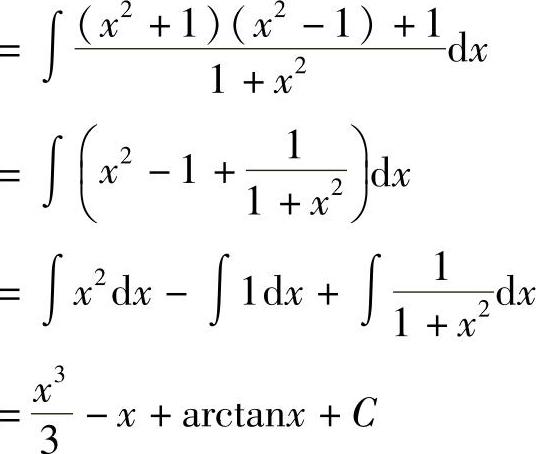
例6 求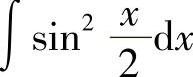 .
.
解 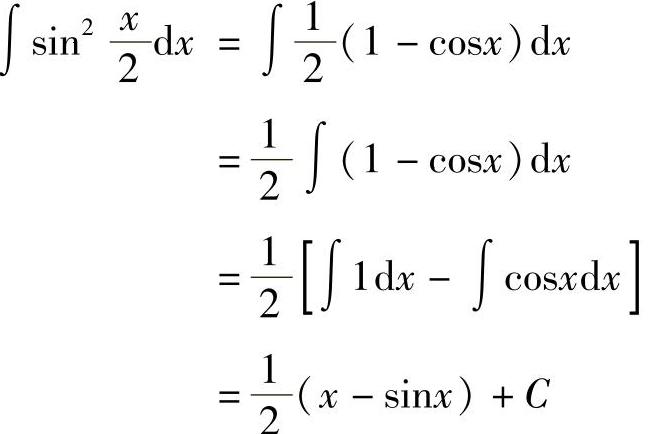
四、不定积分的几何意义
由于函数f(x)的不定积分F(x)+C中含有任意常数,因此在几何上,对于每一个确定的常数值C,都相应地有一条曲线,称为f(x)的积分曲线.显然这样的曲线有无数条,它们可以由曲线y=F(x)沿y轴方向上下移动而得到,称为f(x)的积分曲线族(见图4-1).
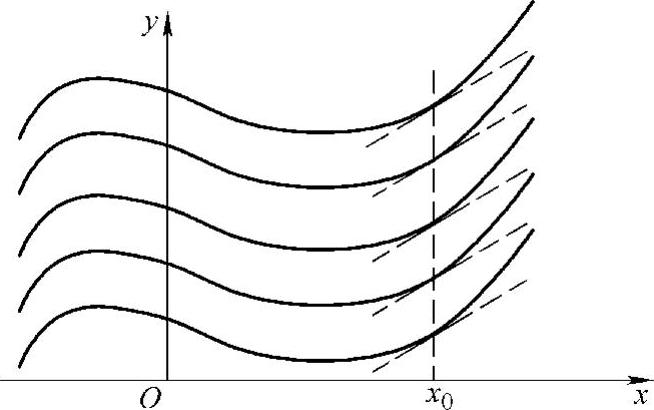
图4-1
积分曲线族中的每一条曲线,对应于同一横坐标x=x0处有相同的斜率f(x0),则在x=x0处它们的切线互相平行(见图4-1).
例7 已知曲线在点P(x,y)的切线斜率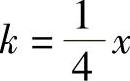 ,且曲线经过点
,且曲线经过点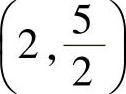 ,求此曲线方程.
,求此曲线方程.
解 设曲线方程为y=f(x),由假设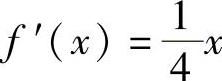 ,有
,有
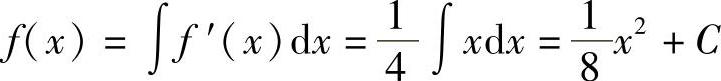
即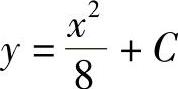 ,C为常数.
,C为常数.
由于曲线经过点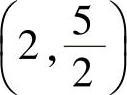 ,以此点坐标代入方程,得
,以此点坐标代入方程,得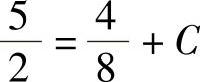 ,解得C=2.
,解得C=2.
因此所求方程为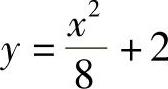 (见图4-2).
(见图4-2).
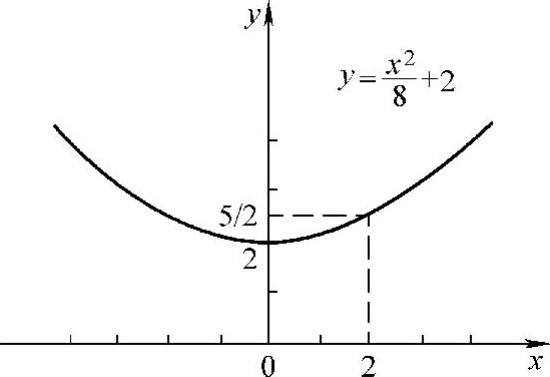
图4-2
