欧拉方程

第五节 欧拉方程

变系数的线性微分方程，一般说来都是不容易求解的.但是有些特殊的变系数线性微分方程，则可以通过变量代换化为常系数线性微分方程，因而容易求解，欧拉方程就是其中的一种.

形如

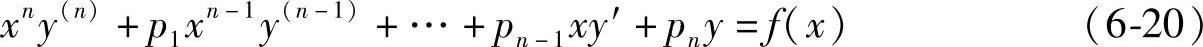
的方程（其中，p₁，p₂…p_n为常数），叫做欧拉方程.

作变换x=e^t或t=lnx，将自变量x换成t，有

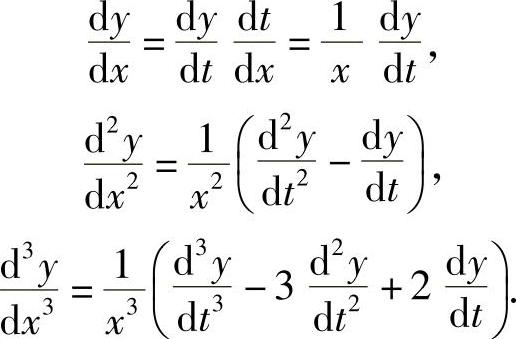
如果采用记号D表示对t求导的运算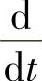，那么上述计算结果可以写成

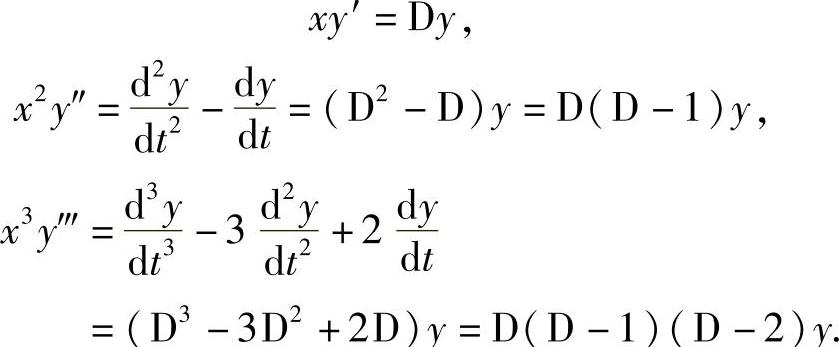
一般地，有

x^ky^（k）=D（D-1）…（D-k+1）y.

把它代入欧拉方程式（6-20），便得一个以为自变量的常系数线性微分方程.在求出这个方程的解后，把t换成lnx（注：这里仅在x＞0范围内求解.如果要在x＜0内求解，则可作变换x=-e^t或t=ln（-x），所得结果与x>0内的结果相类似.），即得原方程的解.

例1 求欧拉方程x³y‴+x²y″-4xy′=3x²的通解.

解 作变换x=e^t或t=lnx，原方程化为

D（D-1）（D-2）y+D（D-1）y-4Dy=3e^2t，

即D³y-2D²y-3Dy=3e^2t，或

方程式（6-21）所对应的齐次方程为

其特征方程为

r³_-2r2-3r=0，它有3个根：r₁=0，r₂=-1，r₃=3.于是方程式（6-22）的通解为

设特解为

y^∗=be^2t=bx²，(https://www.daowen.com)

代入原方程，求得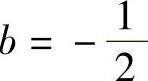，即

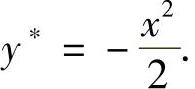
于是，所给欧拉方程的通解为

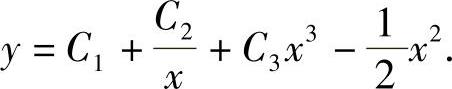
注：这是在x>0内所求得的通解.容易验证，在x＜0内，它也是所给方程的通解.

例2 求方程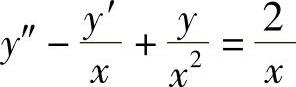的通解.

解 方程变形为

x²y″-xy′+y=2x，它是欧拉方程，作变换x=e^t或t=lnx，原方程化为

D（D-1）y-Dy+y=2e^t.

即D²y-2Dy+y=2e^t.

或

方程式（6-23）所对应的齐次方程为

其特征方程为

r²_-2r+1=0，它有两个根：r₁=r₂=1.于是方程式（6-24）的通解为

Y=（C₁+C₂t）e^t.

设特解为

y^∗=t²Ae^t，

y^∗′=Ae^t（2t+t²），y^∗″=Ae^t（2+2t+2t+t²），将它们代入原方程，求得A=1，即

y^∗=t²e^t.

于是，所给方程的通解为

Y=（C₁+C₂t）e^t+t²e^t=（C₁+C₂lnx）x+xln²x.