导数的运算
一、导数的四则运算
定理2.3 若函数u(x)与v(x)可导,则
1)函数u(x)±v(x)可导,且[u(x)±v(x)]′=u′(x)±v′(x);2)函数u(x)v(x)可导,且[u(x)v(x)]′=u(x)v′(x)+u′(x)v(x);3)函数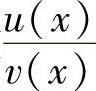 可导(v(x)≠0),且
可导(v(x)≠0),且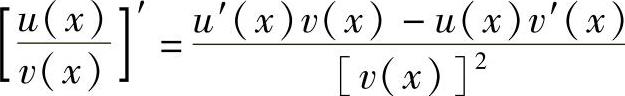 .
.
证 只证2),其余类似可证.
设y=u(x)v(x),有
Δy=u(x+Δx)v(x+Δx)-u(x)v(x)=u(x+Δx)v(x+Δx)-u(x+Δx)v(x)+u(x+Δx)v(x)-u(x)v(x)=u(x+Δx)[v(x+Δx)-v(x)]+v(x)[u(x+Δx)-u(x)]=u(x+Δx)Δv+v(x)Δu
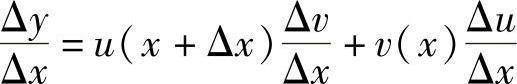
由定理2.2可知函数u(x)连续,即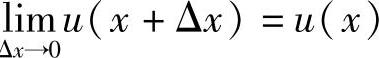 .则
.则
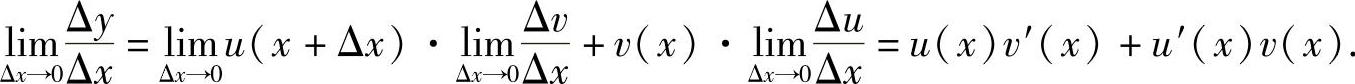
即函数u(x)v(x)可导,且[u(x)v(x)]′=u(x)v′(x)+u′(x)v(x).
推论2.1 若函数u1(x),u2(x),…,un(x)都可导,则函数
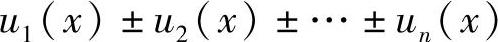
也可导,且[u1(x)±u2(x)±…±un(x)]′=u′1(x)±u2′(x)±…±un′(x).
推论2.2 若函数u1(x),u2(x),…,un(x)都可导,则函数u1(x)u2(x)…un(x)也可导,且
[u1(x)u2(x)…un(x)]′=u′1(x)u2(x)…un(x)+u1(x)u2′(x)…un(x)+…+u1(x)u2(x)…un′(x).
特别地,当v(x)=C是常数时,有[Cu(x)]′=Cu′(x)+u(x)(C)′=Cu′(x).
例1 设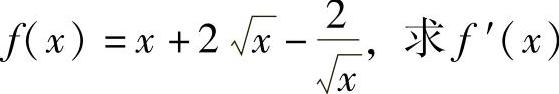 .
.
解 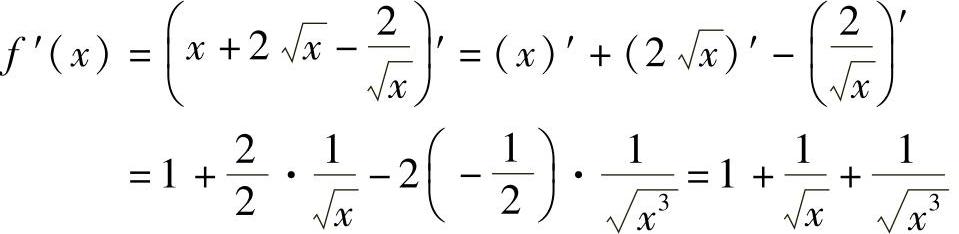
例2 设f(x)=xsinx·lnx,求f′(x).
解 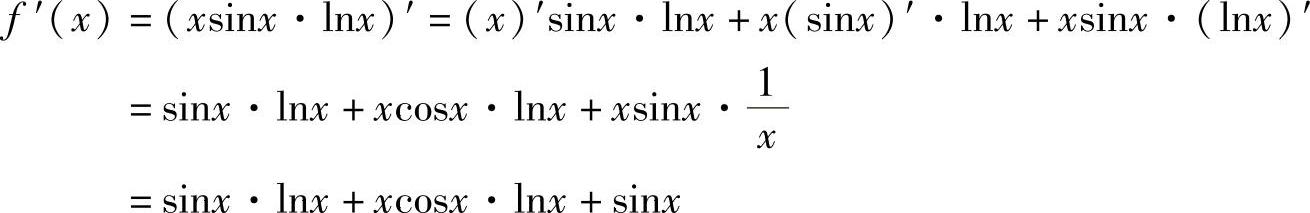
例3 求正切函数tanx与余切函数cotx的导数.
解 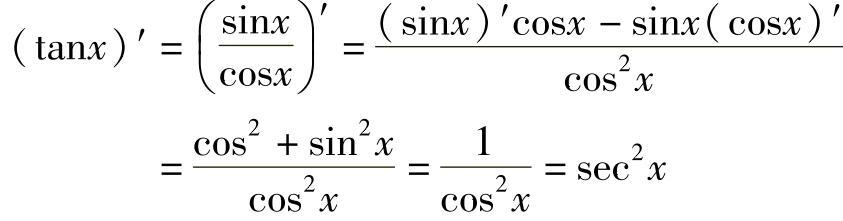
类似地,有(cotx)′=-csc2x.
例4 求正割函数secx与余割函数cscx的导数.
解 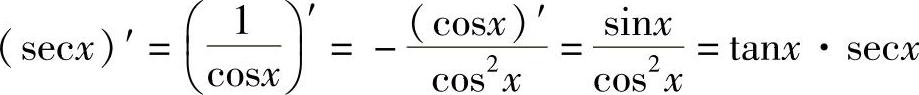
类似地,有(cscx)′=-cotx·cscx.
二、反函数求导法则
定理2.4 若函数f(x)在x的某邻域连续,且严格单调,函数y=f(x)在x可导,且f′(x)≠0,则它的反函数x=φ(y)在y(y=f(x))可导,且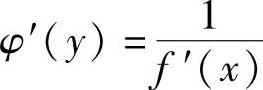 .
.
证 由定理1.1可知,函数y=f(x)在x的某邻域存在反函数x=φ(y).
由于函数y=f(x)在x的某邻域内连续和严格单调,所以它的反函数x=φ(y)在y的某邻域内也连续和严格单调,且有Δy→0⇔Δx→0,Δy≠0⇔Δx≠0,则
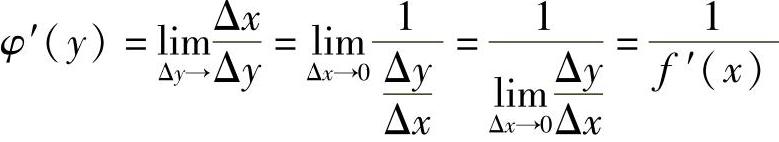
故命题成立.
由于y=f(x)与x=φ(y)互为反函数,上述公式也可以写成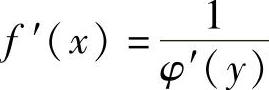 .
.
例5 求指数函数y=ax(a>0,且a≠1)的导数.
解 已知指数函数y=ax是对数函数x=logay的反函数,则
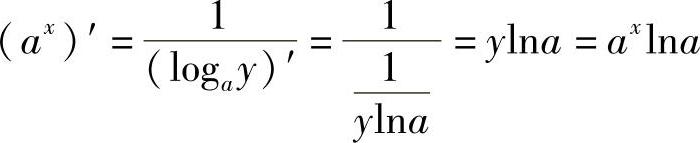
即(ax)′=axlna.
特别地,(ex)′=exlne=ex.
例6 求y=arcsinx的导数.
解 由于y=arcsinx(x∈[-1,1])的反函数是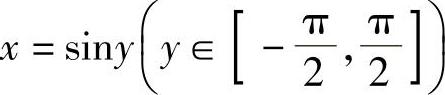 ,则
,则
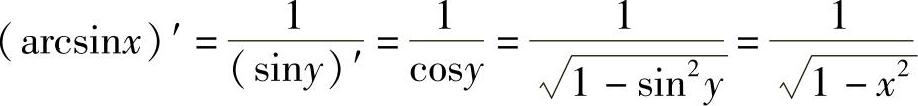
类似地,有 .
.
三、基本初等函数的求导公式
综上所述,列出如下基本公式,它们是导数运算的基础.
1)(C)′=0;2)(xμ)′=μxμ-1;3)(sinx)′=cosx;4)(cosx)′=-sinx;5)(tanx)′=sec2x;6)(cotx)′=-csc2x;7)(secx)′=secx·tanx;8)(cscx)′=-cscx·cotx;9)(ax)′=axlna;10)(ex)′=ex;11)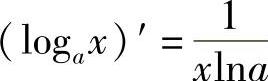 ;12)
;12)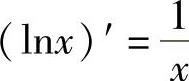 ;13)
;13)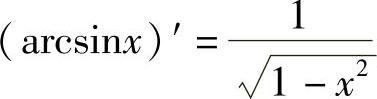 ;14)
;14)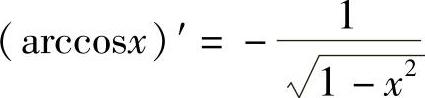 ;15)
;15)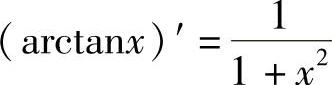 ;16)
;16)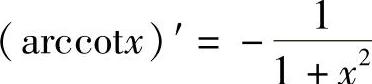 .
.
四、复合函数的导数
定理2.5 若函数u=g(x)在x可导,函数y=f(u)在相应的点u(u=g(x))可导,则复合函数y=f(g(x))在x也可导,且
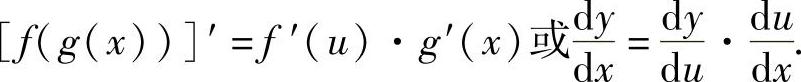
证 当Δu≠0时,有
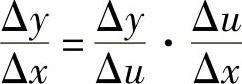
因为u=g(x)在x可导,则u=g(x)在x必连续,所以当Δx→0时,Δu→0.
因此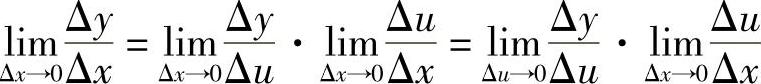
于是有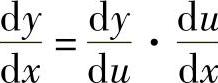 .(https://www.daowen.com)
.(https://www.daowen.com)
当Δu=0时,可以证明该定理仍然成立.
重复使用此定理,显然可以推广到有限次复合.以三个函数为例,若y=f(u),u=φ(v),v=ψ(x)都可导,则
{f[φ(ψ(x))]}′=f′(u)·φ′(v)·ψ′(x).
例7 求 的导数.
的导数.
解  可看成是由y=arctanu与
可看成是由y=arctanu与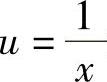 复合而成,则
复合而成,则
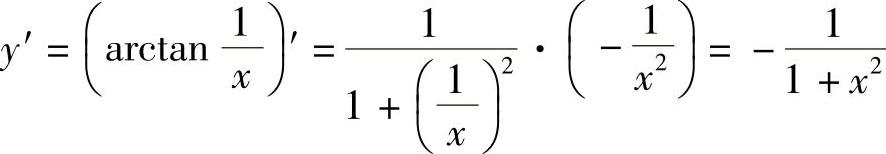
例8 求y=xμ(μ为常数)的导数.
解 y=xμ=eμlnx是由y=eu,u=μ·v,v=lnx复合而成的,则
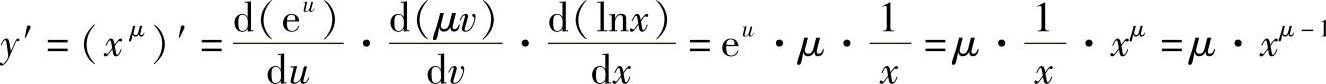
例9 求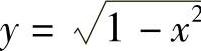 的导数.
的导数.
解 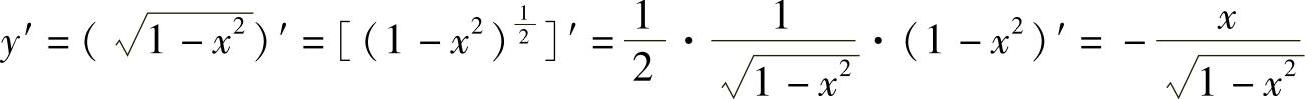
例10 求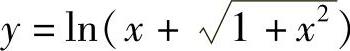 的导数.
的导数.
解 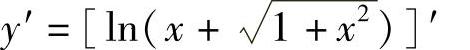
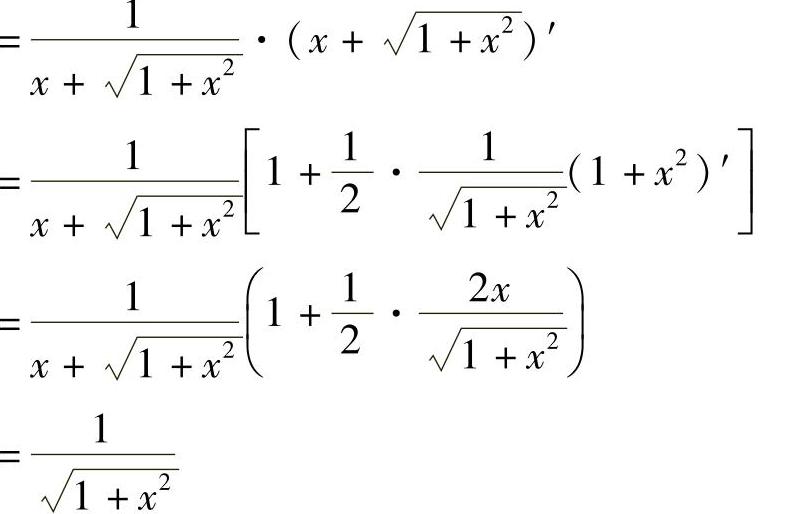
五、隐函数的导数
若由方程F(x,y)=0可确定y是x的函数,则称此函数为隐函数.
由y=f(x)表示的函数,称为显函数.
例如,方程5x2+4y-1=0确定的隐函数,可显化为函数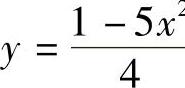 .但是,方程ey+xy-e=0所确定的隐函数y=f(x)却不能被显化.
.但是,方程ey+xy-e=0所确定的隐函数y=f(x)却不能被显化.
例11 求由方程ey+xy-e=0所确定的隐函数y=f(x)的导数.
解 方程两边对x求导(注意y是x的函数),得
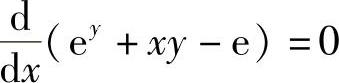
即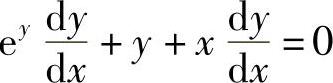
从而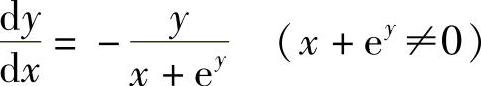 .
.
例12 求椭圆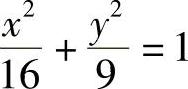 ,在点
,在点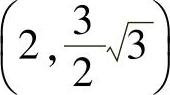 处的切线方程.
处的切线方程.
解 方程两边对x求导,得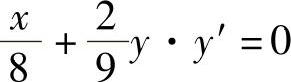
所以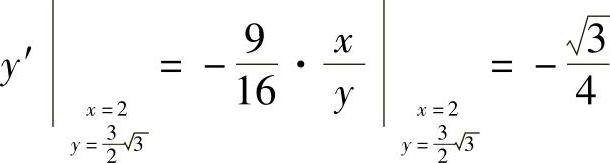 .
.
故切线方程为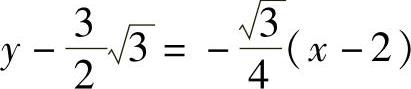
即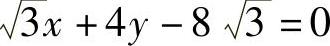 .
.
例13 求函数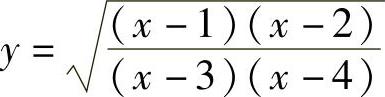 的导数.
的导数.
解 等号两端取对数(假设x>4),得
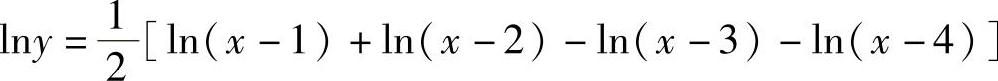
上式两端对x求导,得
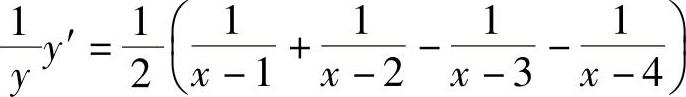
于是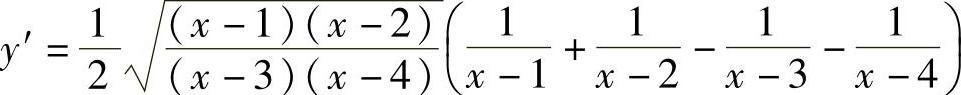 .
.
当x<1时,y=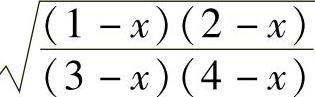 ;当2<x<3时,
;当2<x<3时,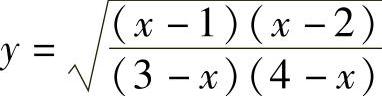 ;用同样的方法可得与上面相同的结果.
;用同样的方法可得与上面相同的结果.
这种先取对数然后再求导的方法称为对数求导法.
例14 求函数y=xsinx(x>0)的导数.
解 这种函数称为幂指函数,需用对数求导法来求它的导数.两边取对数后化为隐函数,得
lny=sinx·lnx
两边对x求导,得
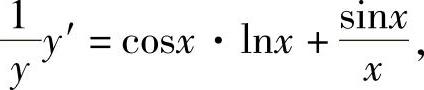
所以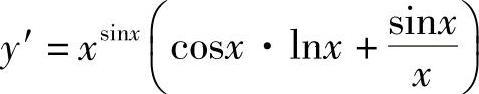 .六、参数方程的导数
.六、参数方程的导数
若参数方程
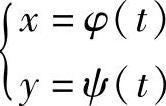
可确定y是x的函数,x=φ(t)与y=ψ(t)都可导,且φ′(t)≠0,如果x=φ(t)存在反函数t=φ-1(x),则y=ψ(φ-1(x)),有
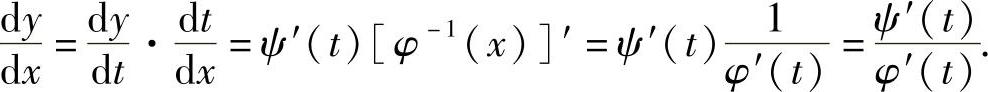
例15 已知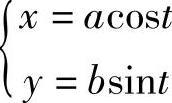 ,求
,求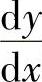 .
.
解 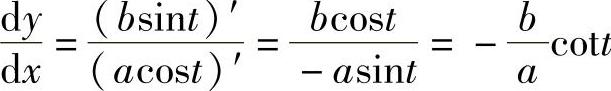 .
.
例16 求摆线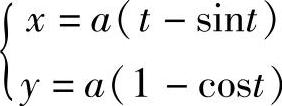 在
在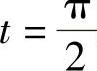 处的切线方程.
处的切线方程.
解 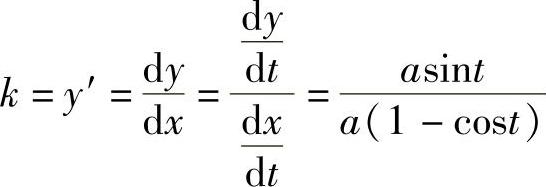
所以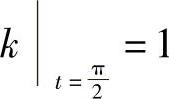
当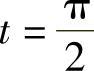 时,
时,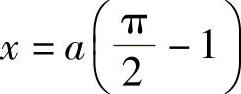 ,y=a,
,y=a,
所以切线方程为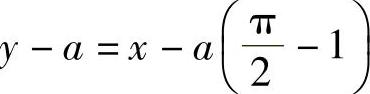 ,
,
即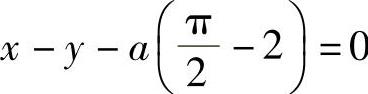 .
.
