分部积分法

第三节 分部积分法

若u=u（x）与v=v（x）都有连续的导数，则由函数乘积的求导公式（uv）′=u′v+uv′，移项得

uv′=（uv）′-u′v.

对这个等式两边求不定积分，得

∫uv′dx=uv-∫u′vdx，即∫udv=uv-∫vdu.

这个公式称为分部积分公式.

一般地，当∫udv不易计算而∫vdu较易计算时，就使用这个公式.

例1 求∫xcosxdx.

解 设u=x，则dv=cosxdx，du=dx，v=sinx，利用分部积分公式得

∫xcosxdx=xsinx-∫sinxdx=xsinx+cosx+C.

例2 求∫xe^xdx.

解 设u=x，dv=e^xdx，则du=dx，v=e^x，则

∫xe^xdx=xe^x-∫e^xdx=xe^x-e^x+C.

例3 求∫x²e^xdx.

解 设u=x²，dv=e^xdx，则du=2xdx，v=e^x，则

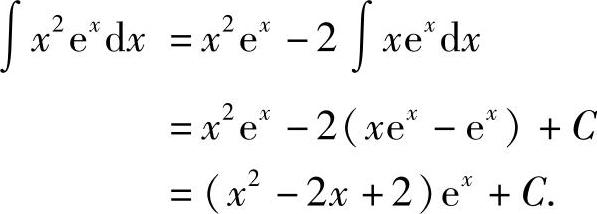
当运算熟练以后，可以不必写出u、v，而直接写出结果.

例4 求∫lnxdx.(https://www.daowen.com)

解 .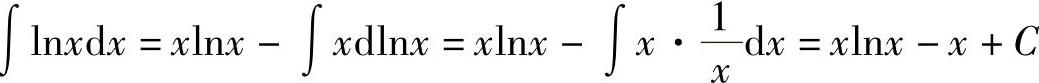

例5 求∫xarctanxdx.

解

例6 求∫e^xsinxdx.

解 ∫e^xsinxdx=∫sinxde^x=e^xsinx-∫e^xdsinx=e^xsinx-∫e^xcosxdx

注意到∫e^xcosxdx与所求积分是同一类型的，需再进行一次分部积分，

.

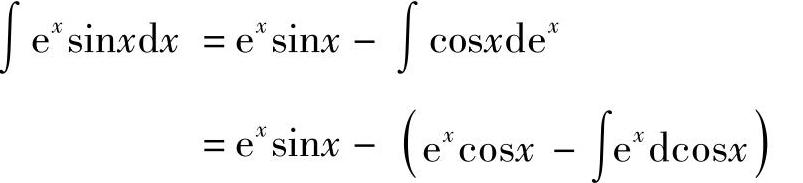
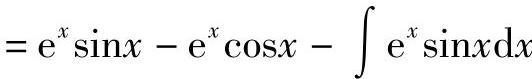则.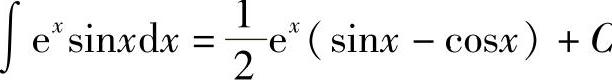

例7 求∫sec³xdx.

解 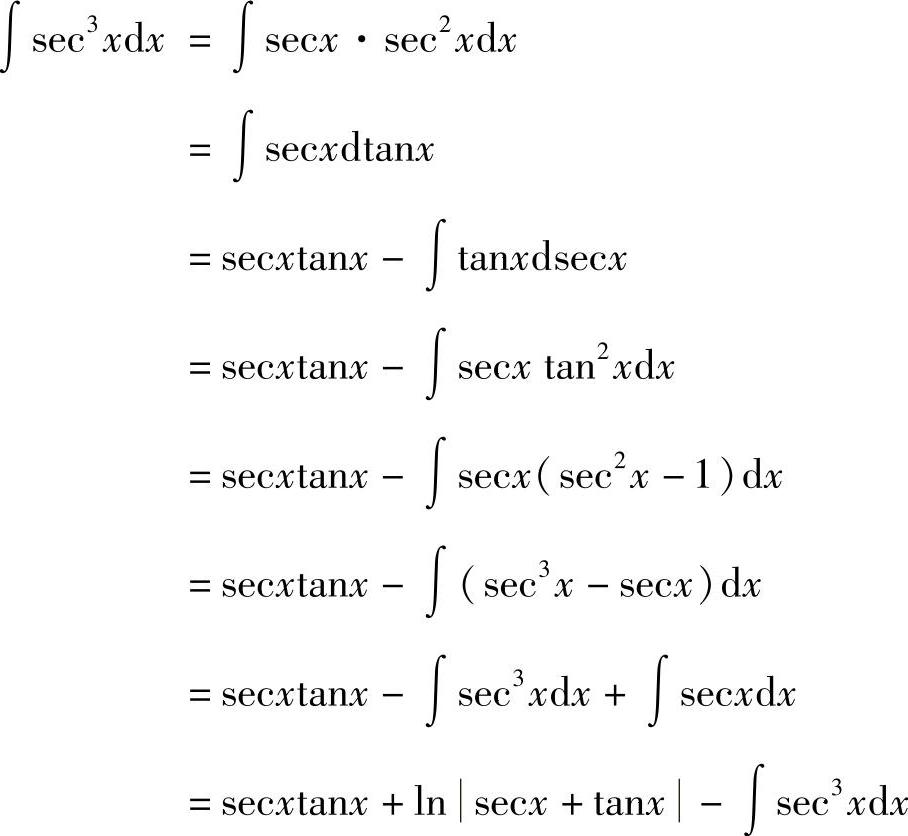，则.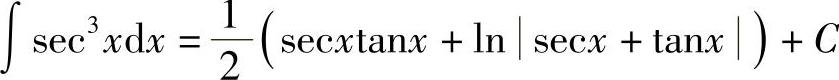

例8 求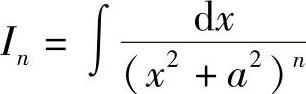（其中，n为正整数）.

解 当n=1时，.

当n＞1时，

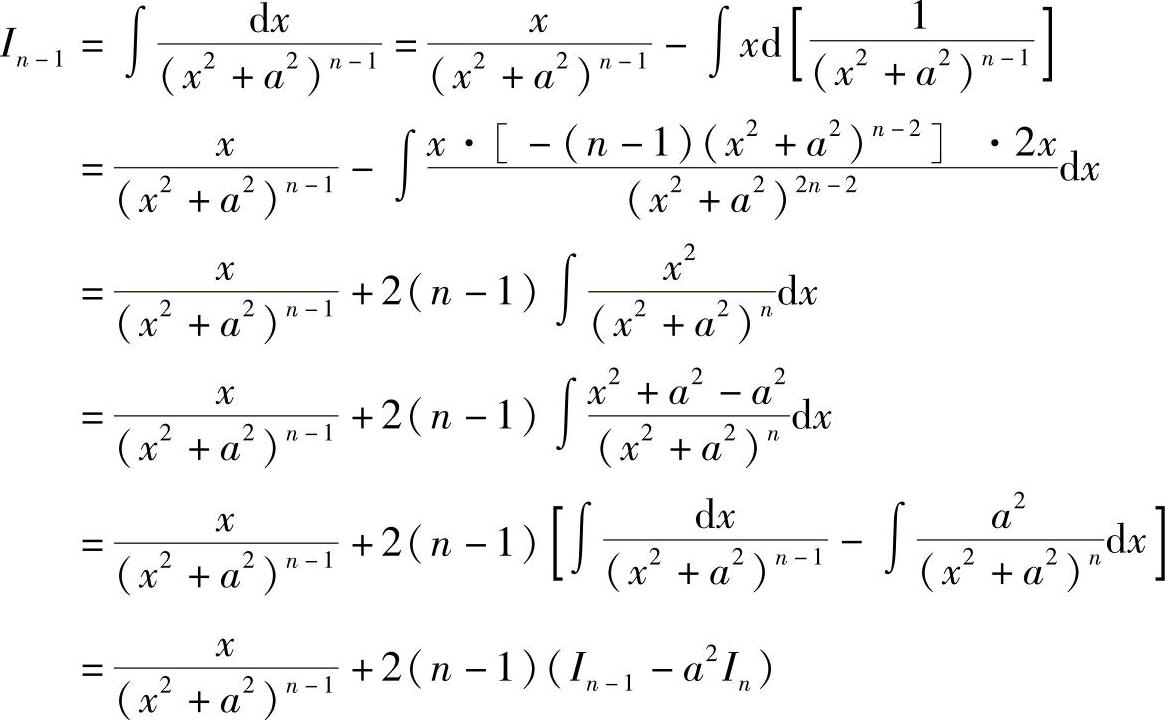
于是.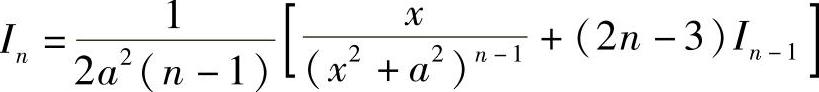

由此递推公式，并由，可得I_n.