习题6.6
习题答案
习题1.1
1.1){x-2<x<-1或x>-1};2){x3≤x≤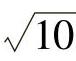 或-
或-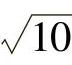 ≤x≤-3}.
≤x≤-3}.
2.{x2kπ≤x≤2kπ+π,k∈Z}.
3.3).
4.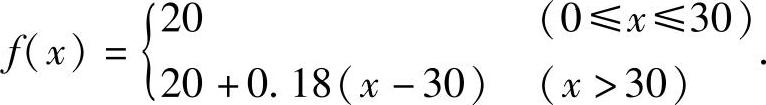
5.f(1)=0,f(0)=-1,f(a)=3a2-2a-1,f(-x)=3x2+2x-1,f(x+1)=3x2+4x,
f(f(x))=27x4-36x3-12x2+16x+4.
6.定义域[-2,3],f(-1)=1,f(0)=2,f(2)=3.
7.定义域[0,+∞),值域[0,+∞),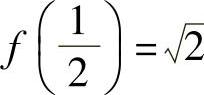 ,
,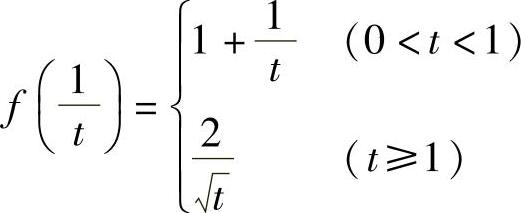 .
.
8.略.
9.略.
10.1)偶;2)奇;3)非奇非偶;4)奇.
11.y=ex+3-2.
12.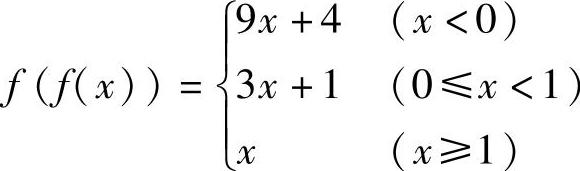 .
.
13.求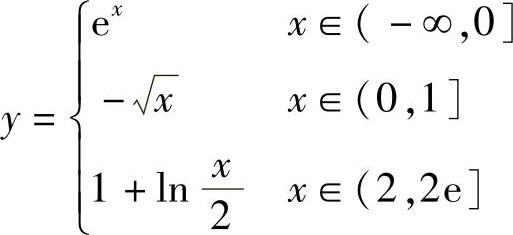
14.1)y=au,u=tanx;2)y=lnu,u=arcsinv,v=x2.
15.略.
16.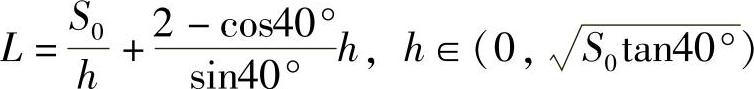 .
.
习题1.2
1.1)1;2)0.
2.略.
3.略.
4.略.
5.略.
6.略.
7.略.
8.略.
习题1.3
1.1.
2.极限不存在.
3.略.
4.略.
5.略.
6.极限不存在.
7.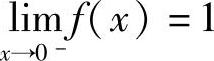 ,
,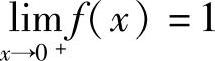 ,
,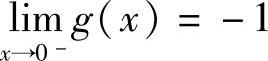 ,
,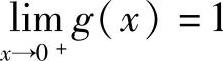 .
.
8.a=-3.
习题1.4
1.1.2.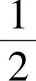 .3.∞.4.
.3.∞.4.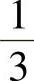 .5.
.5.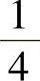 .6.
.6.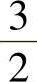 .7.0.8.-
.7.0.8.-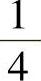 .9.
.9.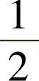 .10.a=-1.
.10.a=-1.
11.1)正确,证明略;2)错误,例如f(x)=sgnx,g(x)=-sgnx,当x→0时的极限都不存在,但f(x)+g(x)当x→0时极限存在;3)错误,例如f(x)=x,g(x)=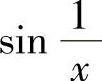 ,
,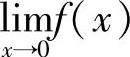 =0,
=0,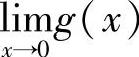 不存在,但
不存在,但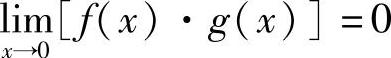 极限存在.
极限存在.
习题1.5
1.1)1;2)3;3)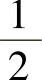 ;4)1;5)1;6)1.
;4)1;5)1;6)1.
2.1)e-k;2)1;3)e2;4)e3;5)1.
3.略.
4.B.
5.a=ln2.
6.ex+1.
习题1.6
1.1)当x→0时是无穷小;当x→1时是无穷大;2)当x→0时是无穷小;当x→+¥时是无穷大.
2.1)高阶;2)低阶;3)同阶;4)同阶.
3.略.
4.1)1;2)
2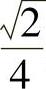 ;3)-
;3)-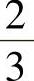 .
.
习题1.7
1.略.
2.连续.
3.1)x=2,无穷间断点;2)x=1,可去间断点;x=2,无穷间断点;3)x=1,跳跃间断点;4)x=0,可去间断点.
4.x=0,无穷间断点;x=1,跳跃间断点.
5.f(0)=0.
6.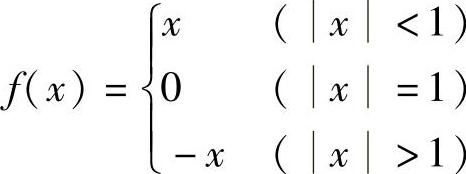 ;x=1和x=-1为第一类间断点.
;x=1和x=-1为第一类间断点.
7.略.
8.略.
习题2.1
1.2.
2.f′(x0).
3.-2.
4.略.
5.x=0.
6.连续但不可导.
7.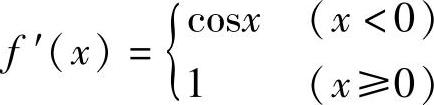 .
.
8. .
.
9.略.
习题2.2
1.1)3x2lnx+x2+2cosx;2)24x3-12x2+6x-2;3)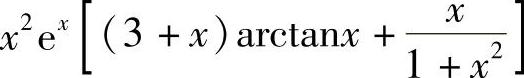 ;4)-
;4)-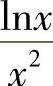 ;5)-
;5)-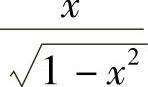 ;6)3x2cosx3;7)3esin3xsin2xcosx8)
;6)3x2cosx3;7)3esin3xsin2xcosx8)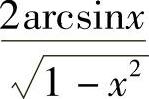 ;9)
;9)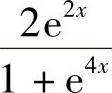 ;10)-
;10)-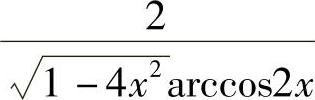 ;11)
;11)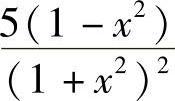 ;12)
;12)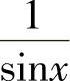 ;13)
;13)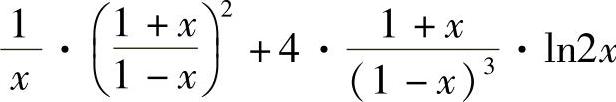 ;14)
;14)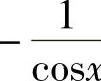 .
.
2.α>0时,连续;α>1时,可导.
3.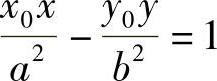 .
.
4.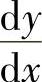 x=0=
x=0=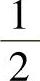 .
.
5.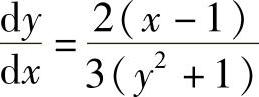 ,
,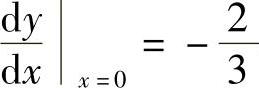 .
.
6.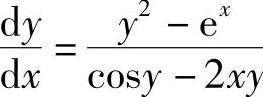 .
.
7.x-y-4=0.
8.1)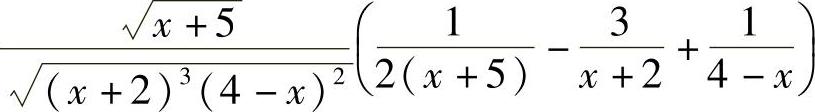 ;2)xx(lnx+1).
;2)xx(lnx+1).
9.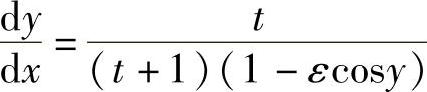 .
.
10. .
.
习题2.3
1.y‴=36,y(4)=0.
2.f″(x)=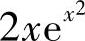 (3+2x2).
(3+2x2).
3.1)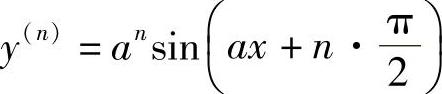 ;2)y(n)=bnebx;3)
;2)y(n)=bnebx;3)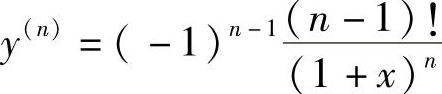 .
.
4.y′(0)=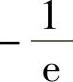 ,y″(0)=
,y″(0)=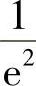 .
.
5.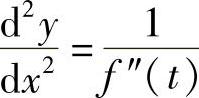 .
.
6.略.
习题2.4
1.Δy=0.0201,dy=0.02.
2.1)ex(sinx+cosx)dx;2)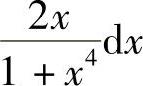 ;3)3cos(3x+1)dx;4)
;3)3cos(3x+1)dx;4)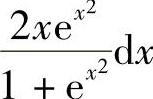 .
.
3.1)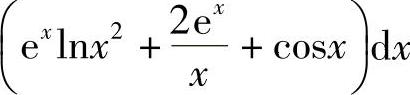 ;2)(a+2bx)eax+bx2dx.
;2)(a+2bx)eax+bx2dx.
4.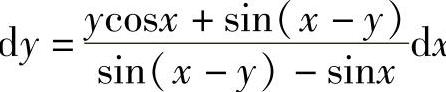 .
.
5.1)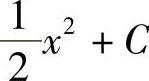 ;2)
;2)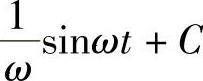 .
.
6.0.485.
7.1.16g.
习题3.1
1.ξ=1.
2.
3.略.
4.略.
5.略.
6.略.
7.略.
8.略.
9.略.
习题3.2
1.1.
2.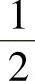 .
.
3.∞.
4.+∞.
5.0.
6.1.
7.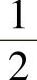 .
.
8.1.
9.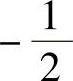
10.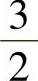 .
.
11.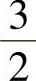 .
.
12.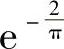 .
.
13.0.
14.0.
15.0.
16.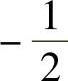 .
.
17.e-1.
习题3.3
1.f(x)=11+7(x-2)+4(x-2)2+(x-3)3.
2.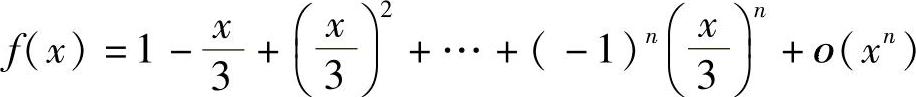 .
.
3.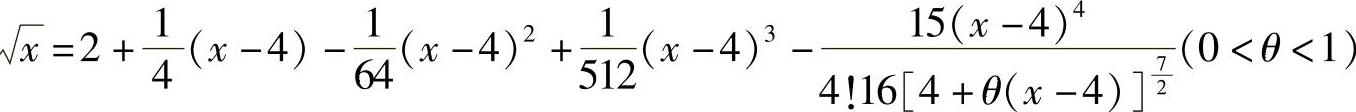 .
.
4.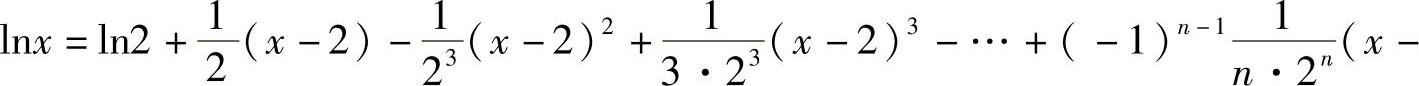
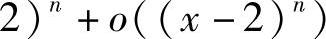 .(https://www.daowen.com)
.(https://www.daowen.com)
5.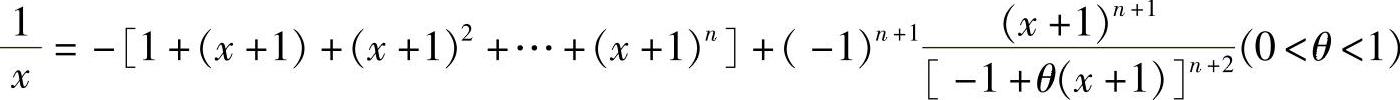 .
.
6.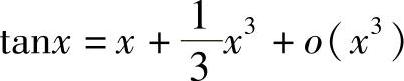 .
.
7.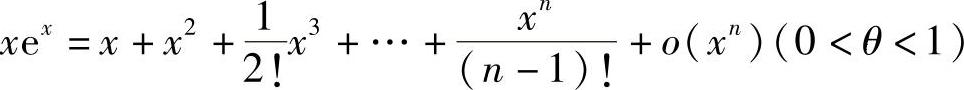 .
.
8. ≈1.645.
≈1.645.
9.1)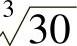 ≈3.10724,|R3|<1.88×10-5.
≈3.10724,|R3|<1.88×10-5.
2)sin18°≈0.3090,|R3|<1.3×10-4.
10.1)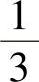 ;2)
;2)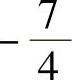 ;3)
;3)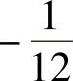 ;4)
;4)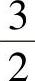 .
.
习题3.4
1.(-∞,-2),(0,+∞)单调递增,(-2,-1),(-1,0)单调递减.
2.(-∞,1)单调递减,(1,+∞)单调递增.
3.(-∞,-1),(1,+∞)凸,(-1,1)凹,拐点(±1,ln2).
4.(-∞,-2)凸,(2,+∞)凹,拐点(2,0).
5.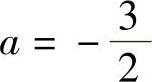 ,
,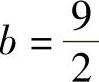 .
.
6.b2-3ac=0.
7.略.
8.当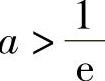 时没有实根;当
时没有实根;当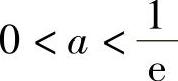 时有两个实根;当
时有两个实根;当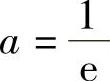 时只有x=e一个实根.
时只有x=e一个实根.
9.y′>0,y″>0.
习题3.5
1.极大值f(1)=2,极小值f(2)=1.
2.极大值f(0)=0,极小值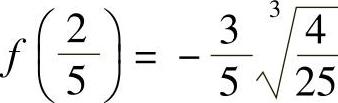 .
.
3.无极大值,极小值f(±1)=1.
4.无极大值,极小值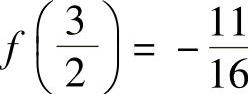 .
.
5.最大值f(3)=11,最小值f(2)=-14.
6.最大值f(2)=1,最小值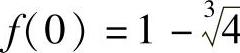 .
.
7.边长为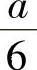 时,容积最大为
时,容积最大为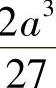 .
.
8.长与宽应分别为4m和2m时,最少长度为8m.
9.r=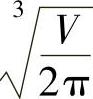 ,h=2
,h=2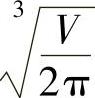 ;d∶h=1∶1.
;d∶h=1∶1.
10.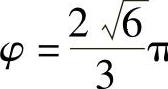 .
.
11.1800元.
习题3.6
1.略.
2.略.
3.略.
4.略.
习题3.7
1.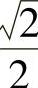 .
.
2.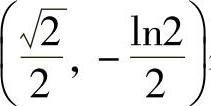 处曲率半径有最小值
处曲率半径有最小值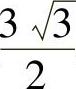 .
.
3.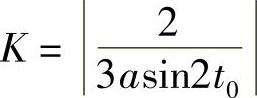 .
.
4.有公切线;凹向一致;曲率相同.
习题4.1
1.1)2x-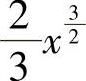 +C;2)
+C;2)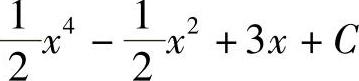 ;3)
;3)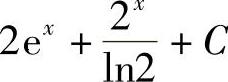 ;4)2(x-arctanx)+C;5)
;4)2(x-arctanx)+C;5)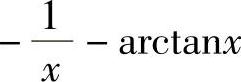 +C;6)tanx-x+C;7)
+C;6)tanx-x+C;7)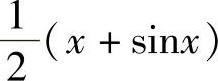 +C;8)
+C;8)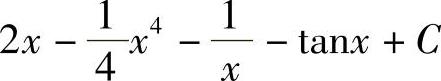 .
.
2.y=x2+1.
3.y=1000+7x+50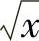 .
.
4.1)27m;2)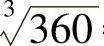 ≈7.11s
≈7.11s
习题4.2
1.1)ln|sinx|+C;2)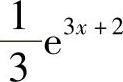 +C;3)
+C;3)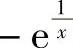 +C;4)
+C;4)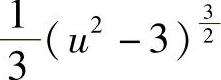
+C;5)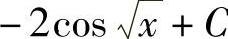 ;6)
;6) +C;7)
+C;7) +C;8)
+C;8)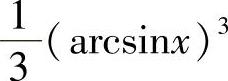 +C;9)
+C;9)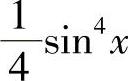 +C;10)
+C;10)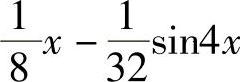 +C;11)
+C;11)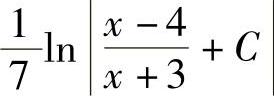 ;12)sin(ex+1)+C;13)
;12)sin(ex+1)+C;13)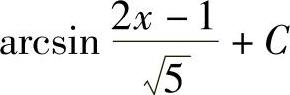 ;14)arccos(e-x)+C.
;14)arccos(e-x)+C.
2.1)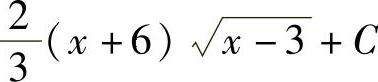 ;2)2[
;2)2[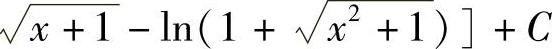 ;3)
;3)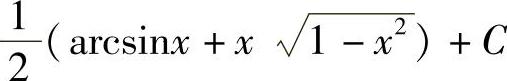 ;4)
;4)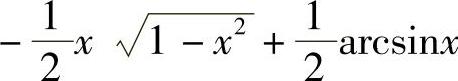 +C;5)
+C;5)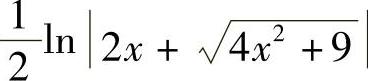 +C;6)
+C;6)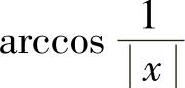 +C;7)
+C;7)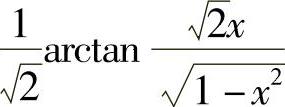 +C;8)
+C;8)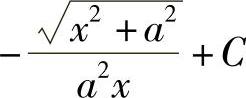 ;9)
;9)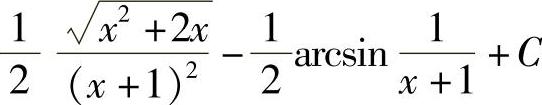 ;10)
;10)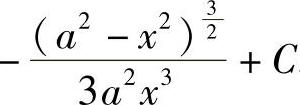 .
.
3.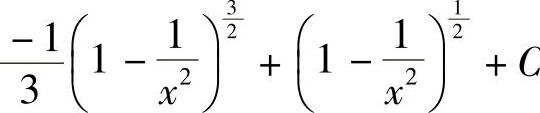 .
.
习题4.3
1.1)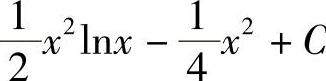 ;2)
;2)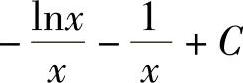 ;3)-x2cosx+2xsinx+2cosx+C;4)
;3)-x2cosx+2xsinx+2cosx+C;4)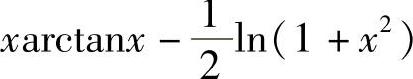 +C;5)xarcsinx+
+C;5)xarcsinx+ +C;6)
+C;6)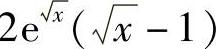 +C.
+C.
2.In=xnex-nIn-1.
3.xf′(x)-f(x)+C.
4.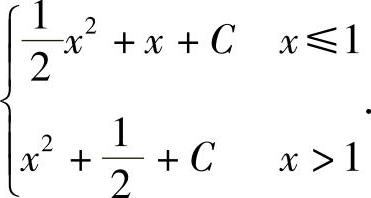
5.exarcsinx+C.
习题4.4
1)-5ln|x|-2+6ln|x|-3+C;2)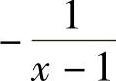 -ln|x|-1+ln|x|+C;3)
-ln|x|-1+ln|x|+C;3)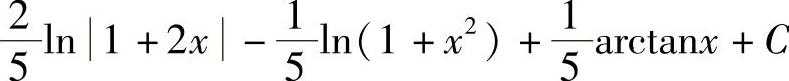 ;4)
;4)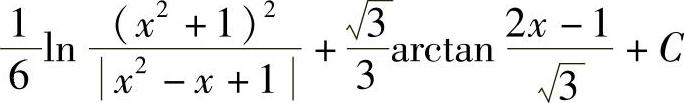 ;5)
;5)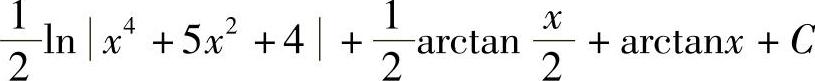 ;6)
;6)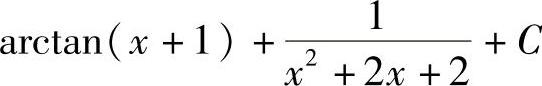 ;7)
;7)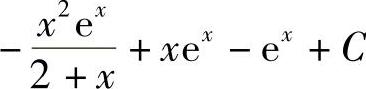 ;8)
;8)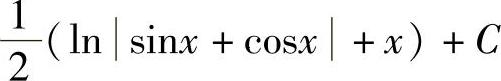 ;9)tanx-secx+C;10)
;9)tanx-secx+C;10)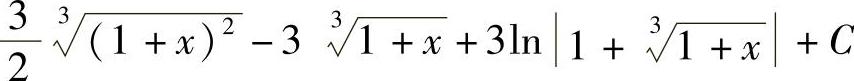 ;11)
;11)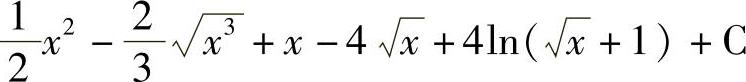 ;12)
;12)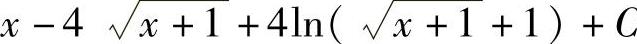 .
.
习题5.1
1.1)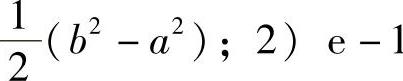 .
.
2.1)0;2)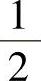 ;3)
;3)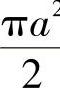 .
.
3.1)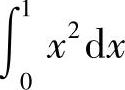 大;2)
大;2)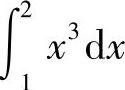 大;3)
大;3)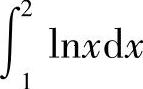 大;4)
大;4)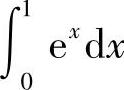 大.
大.
4.1)π≤I≤2π;2)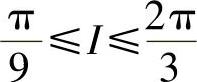 ;3)-2e2≤I≤
;3)-2e2≤I≤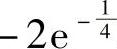 .
.
5.0.
6.略.
习题5.2
1.1)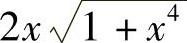 ;2)
;2)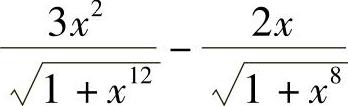 ;3)(sinx-cosx)cos(πsin2x);4)3x2(cosx-1).
;3)(sinx-cosx)cos(πsin2x);4)3x2(cosx-1).
2.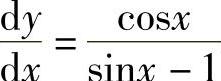 .3.
.3.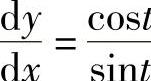 .4.1)1;2)
.4.1)1;2)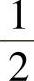 ;3)
;3)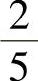 .
.
5.当x=0时.
6.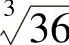 .
.
7.a=-1,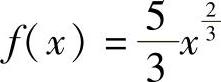 .
.
8.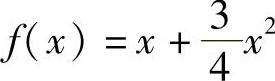 .
.
9.1)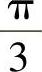 ;2)
;2)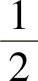 (1+e2);3)2
(1+e2);3)2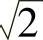 ;4)
;4)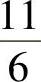 ;5)56
;5)56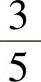 ;6)
;6)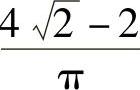 .
.
10.略.
习题5.3
1.1)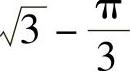 ;2)
;2)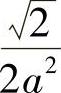 ;3)
;3)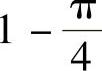 ;4)
;4)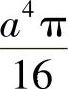 ;5)
;5)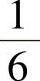 ;6)2(
;6)2(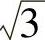 -1).
-1).
2.1)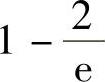 ;2)
;2)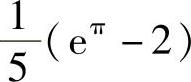 ;3)4(2ln2-1);4)
;3)4(2ln2-1);4)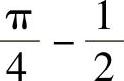 ;5)4π.
;5)4π.
3.1)0;2)0;3)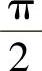 ;4)
;4)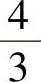 ;5)0.
;5)0.
4.2.
5.tan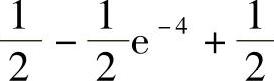 .6.1.
.6.1.
7.略.
8.略.
习题5.4
1.1)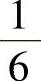 ;2)
;2)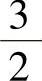 -ln2;3)18;4)e+
-ln2;3)18;4)e+ -2;5)
-2;5)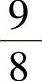 ;6)
;6)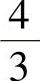 .
.
2.4.
3.c=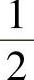 .
.
4.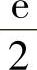 .
.
5.1)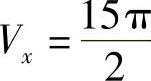 ,Vy=
,Vy=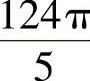 ;2)Vx=
;2)Vx=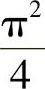 ,Vy=2π;3)Vx=
,Vy=2π;3)Vx=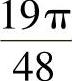 ,Vy=
,Vy=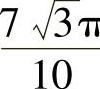 .
.
6.2π2a2b.
7.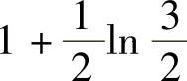 .
.
8.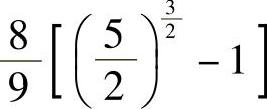 .
.
9.6a.
10.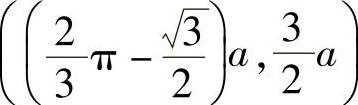 .
.
11.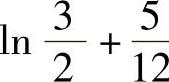 .
.
12.8a.
13.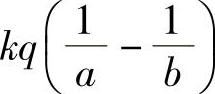 .
.
14.1102.5π.
15.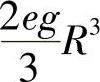 .
.
16.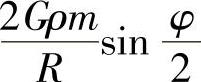 .
.
17.50,100.
18.1)9987.5;2)19850.
19.毛利润:85;纯利润:75.
20.1)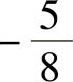 ;2)x=4;3)C(x)=
;2)x=4;3)C(x)=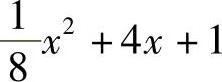 ,
,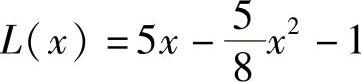 .
.
习题5.5
1.B;
2.A;
3.B;
4.1)收敛;2)发散;3)收敛;4)发散.
5.1)24;2)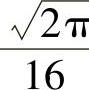 .
.
习题6.1
1.1)一阶;2)二阶;3)一阶;4)三阶.
2.略.
3.1)y2-x2=25(C=-25);2)y=xe2x(C1=0,C2=1).
4.y′=x2.
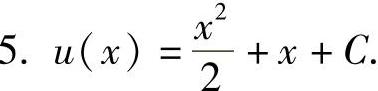
6.f(x)=cosx-xsinx+C.
习题6.2
1.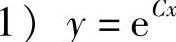 ;2)
;2)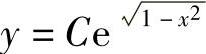 ;3)tanxtany=C;4)sinxsiny=C;5)(ex+1)(ey-1)=C;6)
;3)tanxtany=C;4)sinxsiny=C;5)(ex+1)(ey-1)=C;6) ;7)
;7)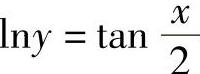 ;
;
8)y2-1=-(x-1)2.
2.1)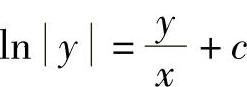 ;2)
;2)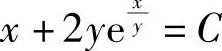 ;3)y2=2x2(lnx+2);4)
;3)y2=2x2(lnx+2);4)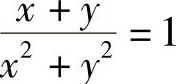 ;
;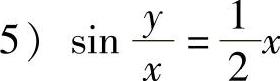 ;6)x2-y2=Cy3.
;6)x2-y2=Cy3.
3.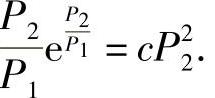
4.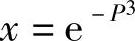 .
.
5.1)y=(x+C)e-sinx;2)2xlny=ln2y+C;3)y=x2(ex-e);
4)ysinx+5ecosx=5ecos1;5)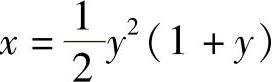 .
.
6.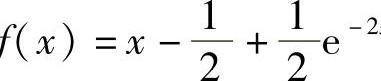 .
.
7.y=2(ex-x-1).
8.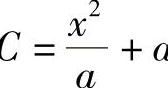
9.1)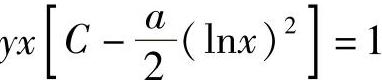 ;2)
;2)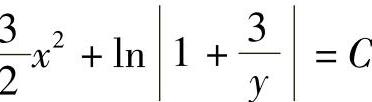 .
.
10.v= ≈269.3(cm/s).
≈269.3(cm/s).
11.R=R0e-0.000433t,时间以年为单位.
12.取O为原点,河岸朝顺水方向为x轴,y轴指向对岸,则所求航线为
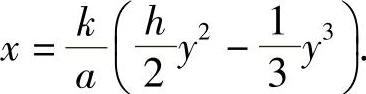
习题6.3
1.1)y=(x-2)ex+C1x+C2;2)y=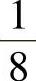 e2x+sinx+C1x2+C2x+C3.
e2x+sinx+C1x2+C2x+C3.
2.1)y=x3+3x+1;2)y=(x-1)ex+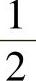 C1x2+C2.
C1x2+C2.
3.1)y=tan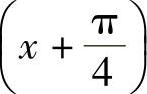 ;2)y2=C1x+C2.
;2)y2=C1x+C2.
4.y=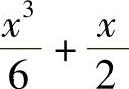 +1.
+1.
5.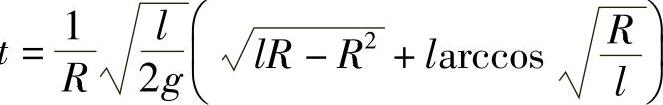 .
.
6.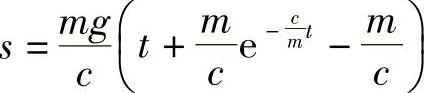 .
.
习题6.4
1.y=C1cosωx+C2sinωx.
2.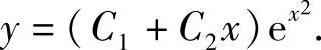
3.y=C1ex+C2x2+3.
4.y=C1cosx+C2sinx+x2-2.
5.1)y=C1e-x+C2e3x;2)y=(C1+C2x)e-2x;3)y=e-x(C1cos2x+C2sin2x);4)y=3e-x-2e-2x;5)y=2cos5x+sin5x;6)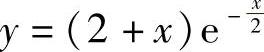 .
.
6.1)y=C1e2x+C2e3x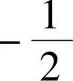 (x2+2x)e2x;2)y=C1e-x+C2e3x-x+
(x2+2x)e2x;2)y=C1e-x+C2e3x-x+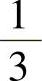 ;3)y=C1cosx+C2sinx+2x+1;4)
;3)y=C1cosx+C2sinx+2x+1;4)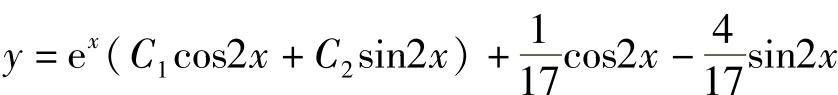 ;5)
;5)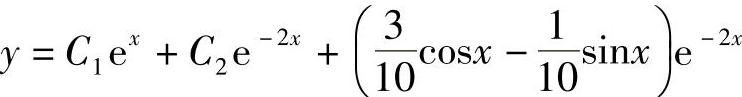 ;6)
;6)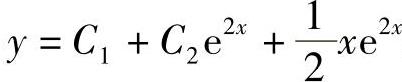 .
.
7.y=(1-2x)ex.
8.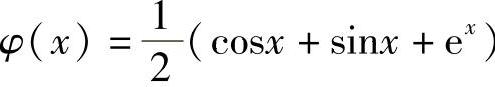 .
.
习题6.5
1.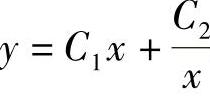 .
.
2.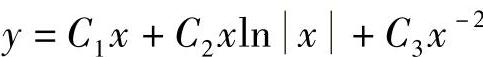 .
.
3.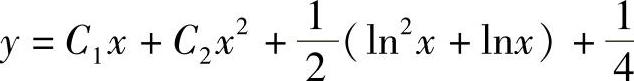 .
.
4.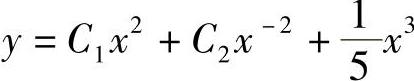 .
.
5.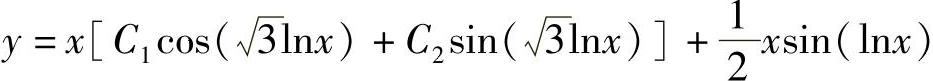 .
.
6.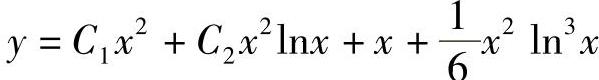 .
.
习题6.6
1.1)7阶;2)4阶.
2.1)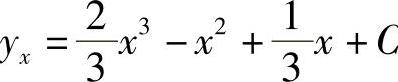 ;2)
;2)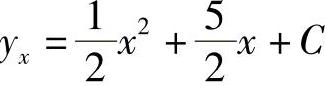 ;3)Yx=C2x-2x2-4x-5;4)
;3)Yx=C2x-2x2-4x-5;4)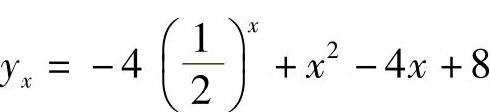 .
.
3.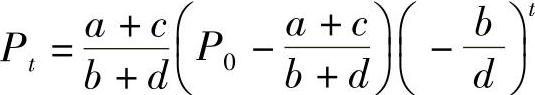 .
.
4.194.95元.
5.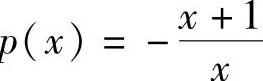 ,
,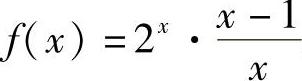 .
.
6.1)yx=A1(-1)x十A24x;
2)yx=(A1+A2x)(-2)x;3)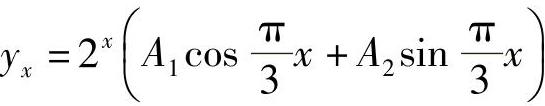 ;4)
;4)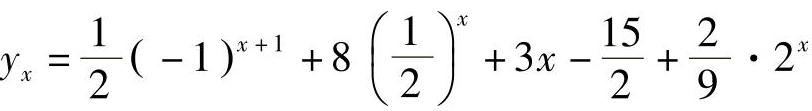 .
.
7.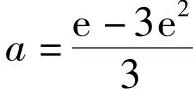 .
.
