习题6.2
1.求下列微分方程的通解或在给定条件下的特解:
1)xy′-ylny=0;2)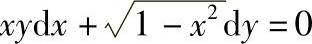 ;3)sec2xtanydx+sec2ytanxdy=0;4)cosxsinydx+sinxcosydy=0;5)(ex+y-ex)dx+(ex+y+ey)dy=0;6)cosydx+(1+e-x)sinydy=0,
;3)sec2xtanydx+sec2ytanxdy=0;4)cosxsinydx+sinxcosydy=0;5)(ex+y-ex)dx+(ex+y+ey)dy=0;6)cosydx+(1+e-x)sinydy=0,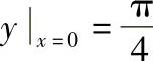 ;7)y′sinx=ylny,
;7)y′sinx=ylny,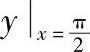 =e;8)dx+xydy=y2dx+ydy,yx=0=0.
=e;8)dx+xydy=y2dx+ydy,yx=0=0.
2.求下列微分方程的通解或在给定条件下的特解:
1)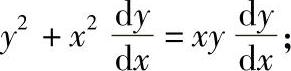 2)
2)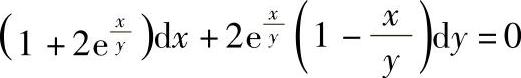 ;3)
;3)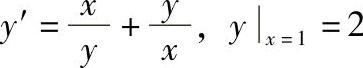 ;4)(x2+2xy-y2)dx+(y2+2xy-x2)dy=0,yx=1=1;5)
;4)(x2+2xy-y2)dx+(y2+2xy-x2)dy=0,yx=1=1;5)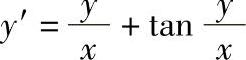 ,
,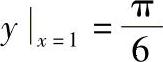 ;6)(y2-3x2)dy+2xydx=0.
;6)(y2-3x2)dy+2xydx=0.
3.设商品A和商品B的售价分别为P1和P2,已知价格P1与价格P2相关,且价格P1相对P2的弹性为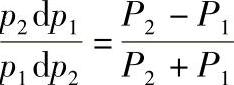 ,求P1与P2的函数关系式.
,求P1与P2的函数关系式.
4.某商品的需求量x对价格P的弹性为η=-3P2,市场对该产品的最大需求量为1(万件),求需求函数.
5.求下列微分方程的通解或在给定条件下的特解:
1)y′+ycosx=e-sinx;2)ylnydx+(x-lny)dy=0;3)xy′-2y=x3ex,y|x=1=0;4)y′+ycotx=5ecosx,y|x=1=0;5)(y2-6x)dy+2ydx=0,y|x=1=1;
6.求连续函数f(x),使它满足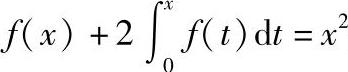 .(https://www.daowen.com)
.(https://www.daowen.com)
7.求一曲线方程,该曲线通过原点,并且它在点(x,y)处的切线斜率等于2x+y.
8.已知生产某产品的固定成本为a>0,生产x单位的边际成本与平均单位成本之差为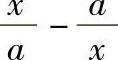 ,且当产量的数值等于a时,相应的总成本为2a,求总成本C与产量x的函数关系.
,且当产量的数值等于a时,相应的总成本为2a,求总成本C与产量x的函数关系.
9.求下列微分方程的通解:1)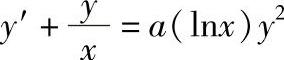 ;
;
2)y′-3xy=xy2.
10.质量为1g的质点受外力作用做直线运动,外力和时间成正比,和质点运动的速度成反比.在t=10s时,速度等于50cm/s,外力为4g·cm/s2,问从运动开始经过一分钟后的速度是多少?
11.镭的衰变有以下的规律:镭的衰变速度与它的现存量R成正比.由经验材料得知,镭经过1600年后,只余原始量R0的一半.试求镭的现存量R与时间t的函数关系.
12.小船从河边点O处出发驶向对岸(两岸为平行直线).设速度为a,船行方向始终与河岸垂直,又设河宽为h,河中任意一点处的水流速度与该点到两岸距离的乘积成正比(比例系数为k).求小船的航行路线.
