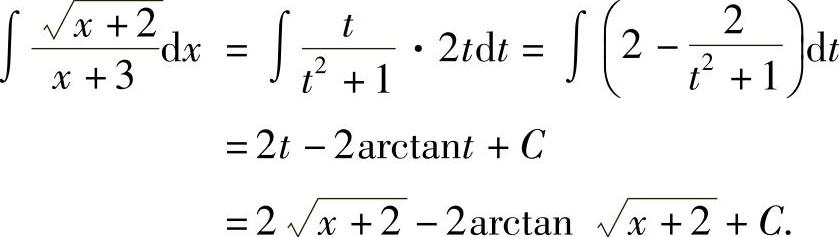有理函数积分
一、有理函数的积分
两个多项式的商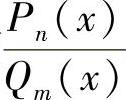 称为有理函数,又称有理分式.
称为有理函数,又称有理分式.
其中,Pn(x)、Qm(x)分别是关于x的n次和m次的实系数多项式.
当n<m时,称为有理真分式,否则称为有理假分式.对于有理假分式,由于n≥m,应用多项式的除法,可得
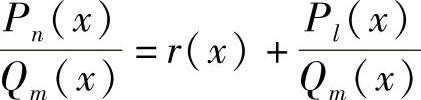
其中,r(x)是多项式,而Pl(x)是次数小于Qm(x)的多项式.
即有理假分式总能化为多项式与有理真分式之和.多项式的积分容易求得,故只需讨论有理真分式的积分.
设有理真分式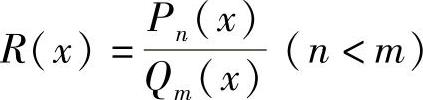 ,若分母Qm(x)因式分解为
,若分母Qm(x)因式分解为
Qm(x)=a0(x-a)α(x-b)β…(x2+px+q)λ…(x2+rx+s)μ…
其中,α,β,…,λ,μ,…是正整数,各二次多项式无实根,则R(x)可唯一地分解成下面形式的分式之和.
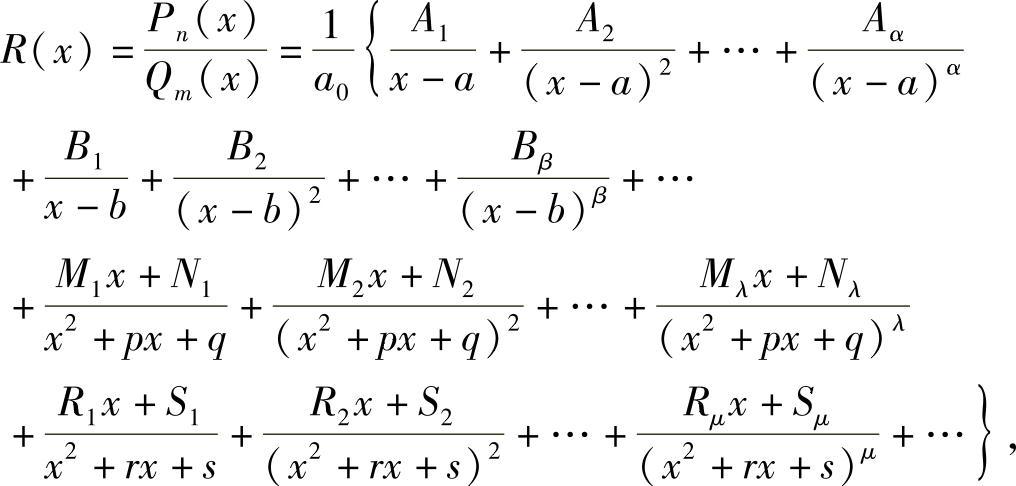
其中,A1,A2,…;B1,B2,…;M1,M2,…;N1,N2,…;R1,R2,…;S1,S2,…都是实常数,可以由待定系数法确定.
这样,求有理真分式的积分最终归结为求下面四类最简分式的积分:
1)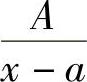 ;2)
;2)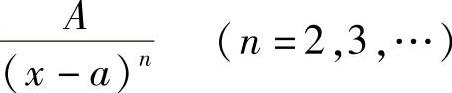 ;3)
;3)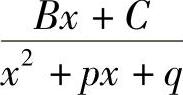 ;4)
;4)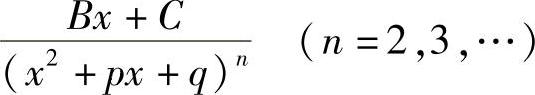 .
.
其中,A、B、C、a、p、q均为常数,且二次式x2+px+q无实根.
例1 求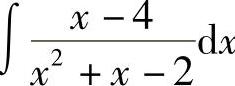 .
.
解 设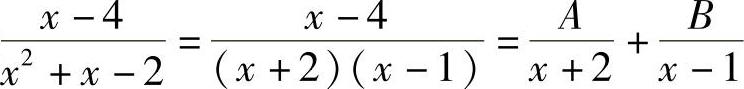 ,由x-4=A(x-1)+B(x+2)=(A+B)x+2B-A,有
,由x-4=A(x-1)+B(x+2)=(A+B)x+2B-A,有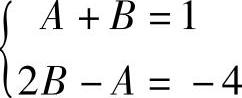 ,解得
,解得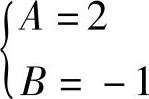 ,故
,故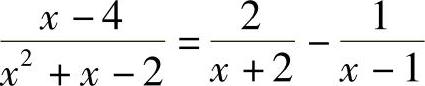 ,从而
,从而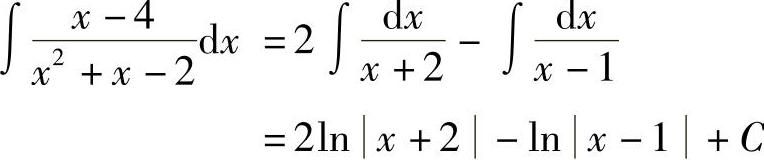 .
.
例2 求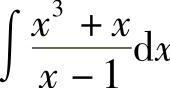 .
.
解 因为x3+x=(x2+x+2)(x-1)+2,所以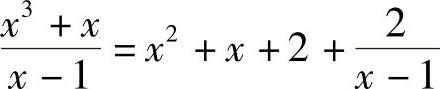 ,则
,则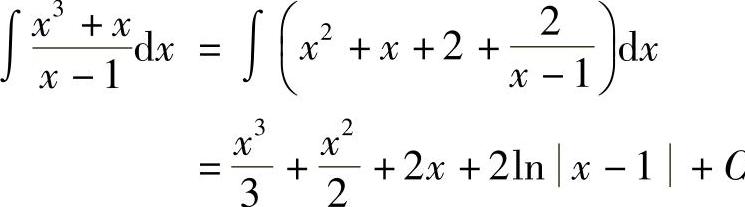 .
.
例3 求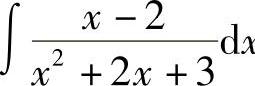 .
.
解 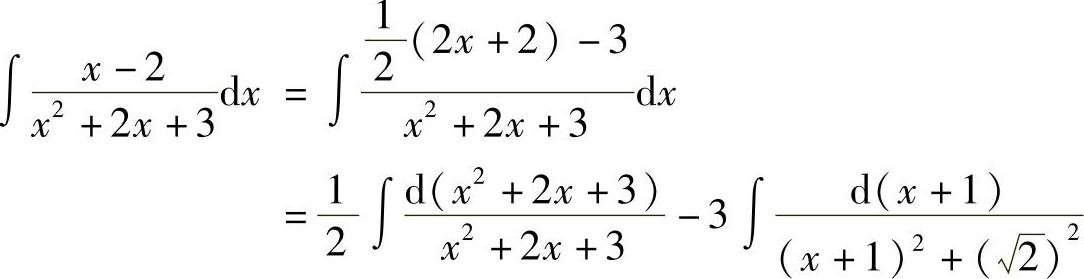
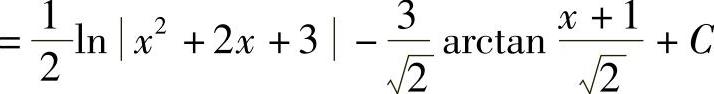 .(https://www.daowen.com)
.(https://www.daowen.com)
例4 求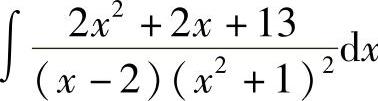 .
.
解 设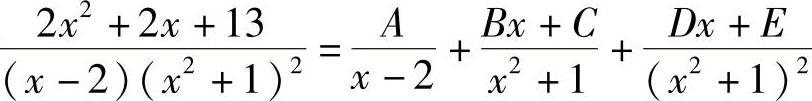 ,解得A=1,B=-1,C=-2,D=-3,E=-4,有
,解得A=1,B=-1,C=-2,D=-3,E=-4,有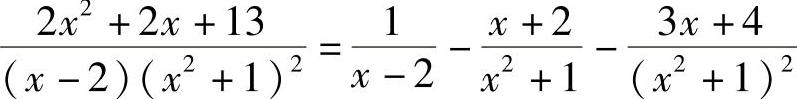 ,于是
,于是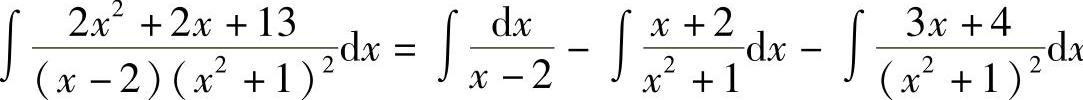 .
.
分别求上式等号右端的每一个不定积分: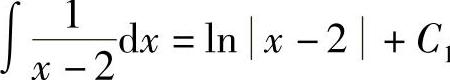 ,
,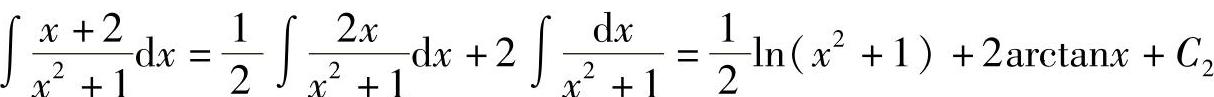 ’
’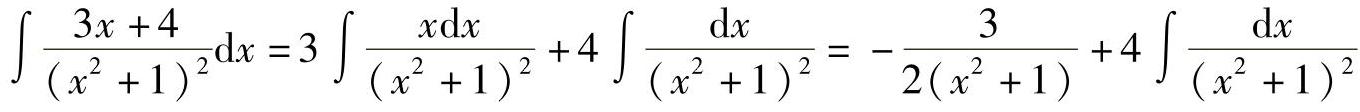 ’
’
由4.3节例8的递推公式有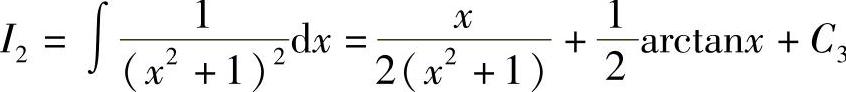 .
.
所以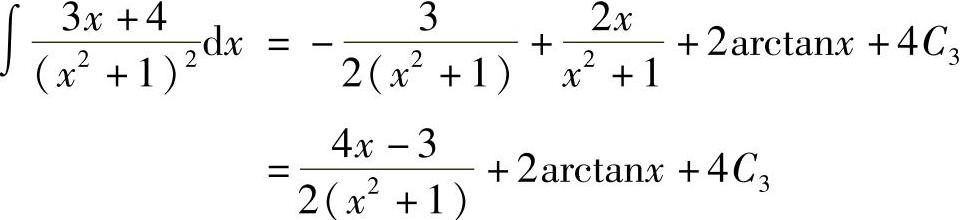
于是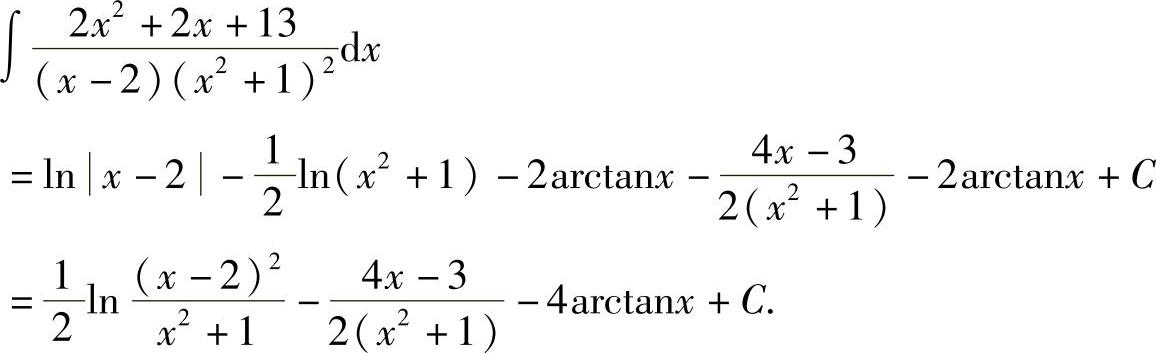 二、可化为有理函数的积分
二、可化为有理函数的积分
例5 求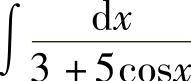 .
.
解 由三角函数的万能公式可知,sinx和cosx都可表示为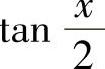 的有理式,令
的有理式,令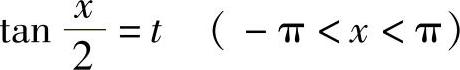 ,则有x=2arctant,
,则有x=2arctant,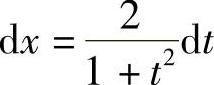 ,
,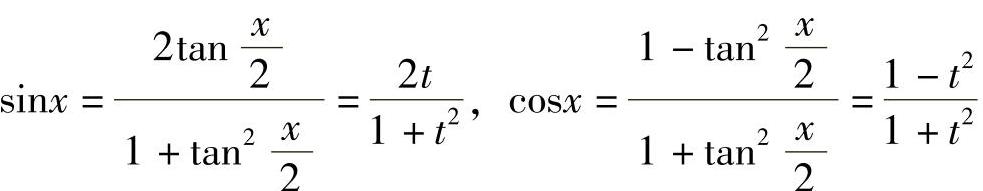 ,
,
则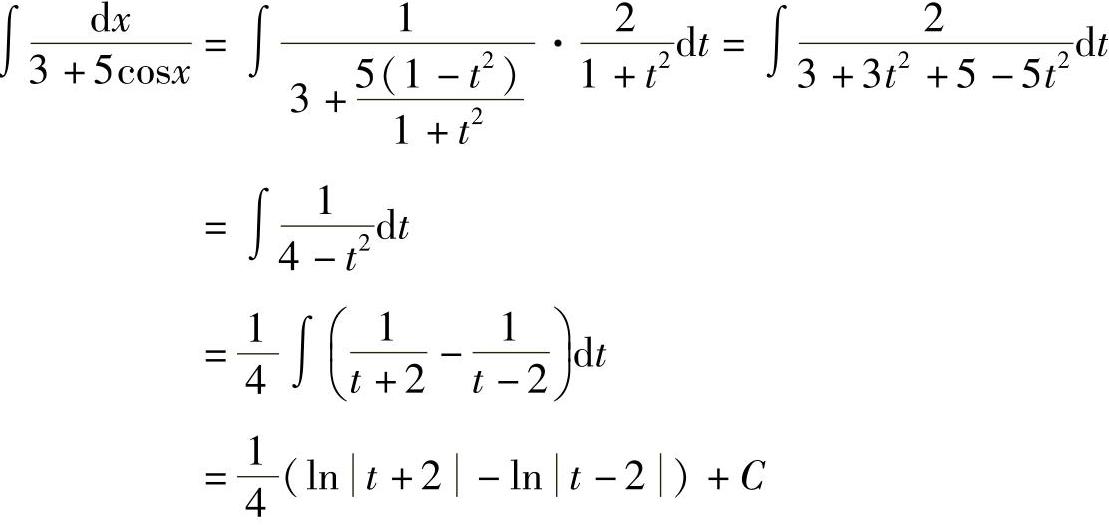
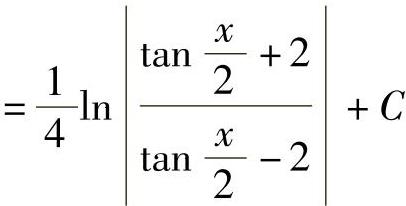 .
.
例6 求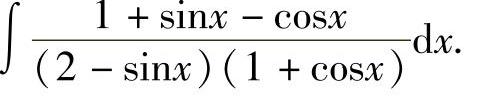
解 令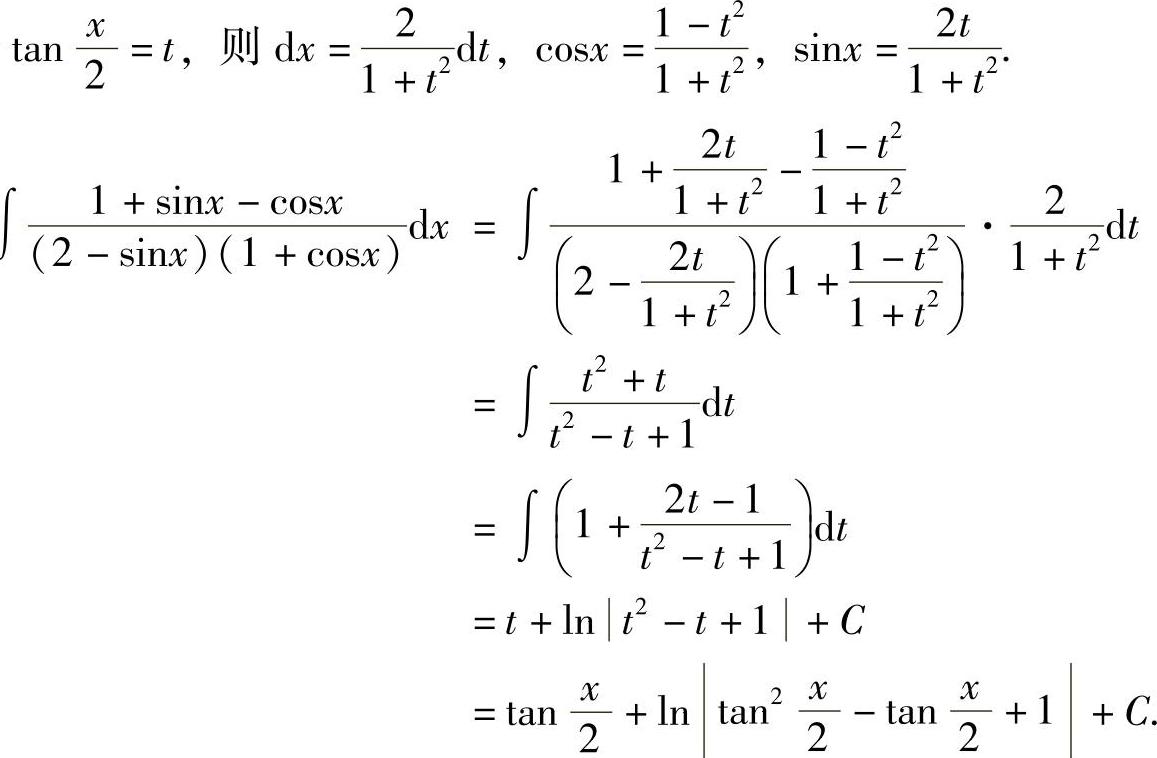
例7 求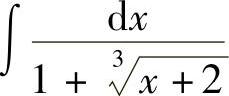 .
.
解 设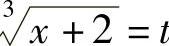 ,则
,则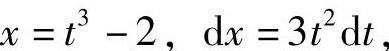
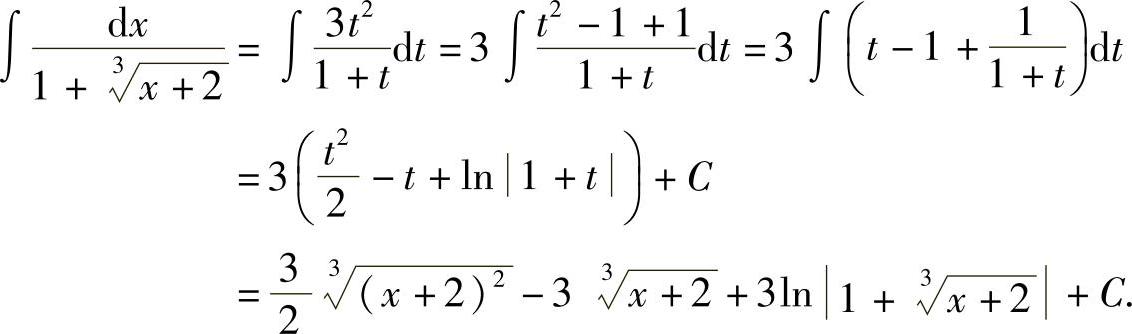
例8 求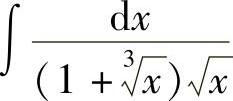 .
.
解 为了能同时消去两个根式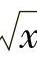 和
和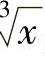 ,设
,设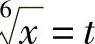 ,则dx=6t5dt,
,则dx=6t5dt,
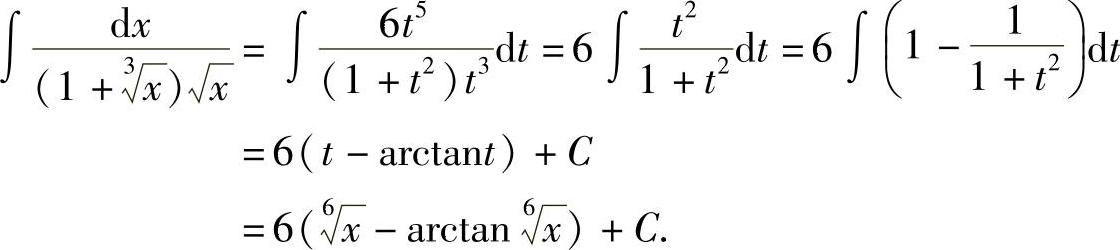
例9 求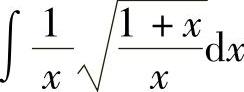 .
.
解 令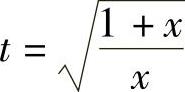 ,则
,则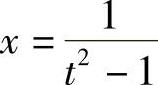 ,
,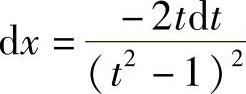 ,
,

例10 求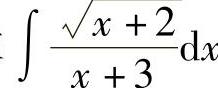 .
.
解 设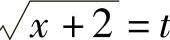 ,则
,则