二阶常系数线性齐次微分方程的解法
一、线性微分方程解的性质与解的结构
1.n阶线性微分方程
形如y(n)+p1(x)y(n-1)+…+pn-1(x)y′+pn(x)y=f(x)的方程称为n阶线性微分方程.其中,p1(x),…,pn(x),f(x)都是x的连续函数.
若f(x)≡0,则称为n阶线性齐次方程.反之,称为n阶线性非齐次方程.
当n=2时,方程变为二阶线性微分方程
y″+p1(x)y′+p2(x)y=f(x).
下面以二阶线性微分方程为例讨论二阶线性微分方程的性质及解法.
2.二阶线性齐次方程解的性质
定理6.1 设y1,y2是二阶线性齐次方程的两个解,则y1与y2的线性组合
y=c1y1+c2y2
也是该方程的解.其中c1、c2是任意常数.
证 由假设有y″1+p1(x)y′1+p2(x)y1≡0,y″2+p1(x)y2′+p2(x)y2≡0,将y=C1y1+C2y2代入y″+p1(x)y′+p2(x)y=0,有
(C1y1+C2y2)″+p1(x)[C1y1+C2y2]′+p2(x)[C1y1+C2y2]=C1[y″+p1(x)y′1+p2(x)y1]+C2[y″2+p1(x)y2′+p2(x)y2].
由于上式右端方括号中的表达式都恒等于零,因而整个式子恒等于零,即y=C1y1+C2y2是方程的解.
如果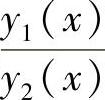 不恒等于非零常数,称为y1(x)与y2(x)线性无关的,否则称y1(x)与y2(x)线性相关.
不恒等于非零常数,称为y1(x)与y2(x)线性无关的,否则称y1(x)与y2(x)线性相关.
例1 函数y1=ex与y2=e-x在任意区间上都是线性无关的.
事实上,比式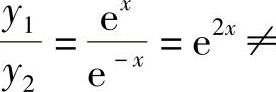 常数,在任意区间上都成立.
常数,在任意区间上都成立.
定理6.2 如果y1(x)与y2(x)是齐次方程的两个线性无关的解,则
y=C1y1+C2y2是该齐次方程的通解.
例2 由函数y1=x与y2=x2是方程x2y″-2xy′+2y=0(x>0)的解,易知y1与y2线性无关,所以方程的通解为y=C1x+C2x2.
3.线性非齐次方程解的结构
定理6.3 设y1(x)是非齐次方程的一个特解,y2(x)是相应的齐次方程的通解,则Y=y1(x)+y2(x)是非齐次方程的通解.
证 因为y1(x)是非齐次方程的解,即
y″1+p1(x)y′1+p2(x)y1=f(x),又因为y2(x)是相应的齐次方程的解,即
y″2+p1(x)y2′+p2(x)y2=0,对于Y=y1+y2有
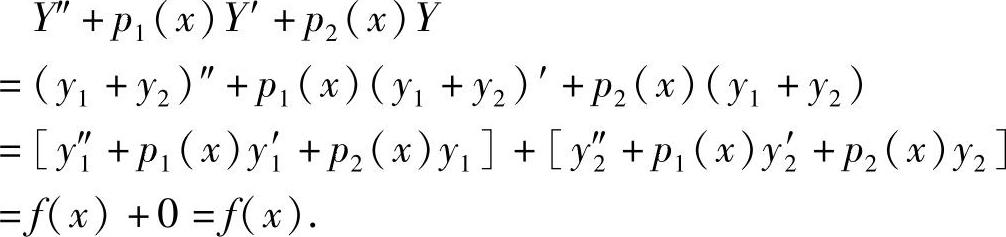
因此y1+y2是方程是非齐次方程的解.又因为y2是方程对应齐次方程的通解,故y1+y2也含有两个任意常数,所以它是非齐次方程的通解.
定理6.4 (叠加原理)设y1(x)与y2(x)分别是方程
y″+p1(x)y′+p2(x)y=f1(x)
和
y″+p1(x)y′+p2(x)y=f2(x)的解,则y1(x)+y2(x)是方程y″+p1(x)y′+p2(x)y=f1(x)+f2(x)的解.二、二阶常系数线性齐次微分方程的解法
y″+py′+qy=0的特点:左端是y″,py′和qy三项之和,而右端为零.
什么样的函数具有这个特征呢?读者自然会想到指数y=erx(r为待定常数).将y=erx,y′=rerx和y″=r2erx代入方程
y″+py′+qy=0,有
r2erx+prerx+qerx=0,即
erx(r2+pr+q)=0.
因为erx≠0,故必然有r2+pr+q=0.这是一元二次方程,它有两个根
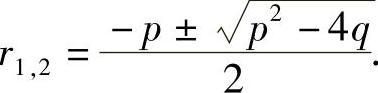
因此,只要r1和r2分别为方程r2+pr+q=0的根,则y=er1x和y=er2x就都是方程y″+py′+qy=0的特解.代数方程r2+pr+q=0称为微分方程y″+py′+qy=0的特征方程,它的根称为特征根.
下面分三种情况讨论齐次方程的通解.
1.特征方程有两个相异实根r1和r2的情形
这时y1=er1x和y2=er2x就是齐次微分方程的两个特解,由于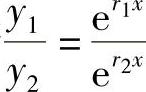 =e(r1-r2)x≠
=e(r1-r2)x≠
常数,所以y1、y2线性无关,故齐次微分方程的通解为y=c1er1x+c2er2x.
例3 求y″+3y′-4y=0的通解.
解 特征方程为r2+3r-4=(r+4)(r-1)=0,
特征根为r1=-4,r2=1.
故方程的通解为y=C1e-4x+C2ex.
2.特征方程有两个相等实根r=r1=r2的情形
这时仅得到齐次微分方程一个特解y1=erx,要求通解还需找一个与y1=erx线性无关的特解y2.
令 =u(x),其中,u(x)为待定函数.即y2=u(x)erx,则y2′=erx[ru(x)+u′(x)],y″2=erx[r2u(x)+2ru′(x)+u″(x)],
=u(x),其中,u(x)为待定函数.即y2=u(x)erx,则y2′=erx[ru(x)+u′(x)],y″2=erx[r2u(x)+2ru′(x)+u″(x)],
代入齐次微分方程,整理后得erx[u″(x)+(2r+p)u′(x)+(r2+pr+q)u(x)]=0.
因为erx≠0,且r为特征方程的二重根,故r2+pr+q=0且2r+p=0,于是上式成为u″(x)=0.取u(x)=x,则满足u″(x)=0,且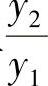 =x≠常数.故齐次微分方程的通解为(https://www.daowen.com)
=x≠常数.故齐次微分方程的通解为(https://www.daowen.com)
y=C1erx+C2xerx=erx(C1+C2x).
例4 求方程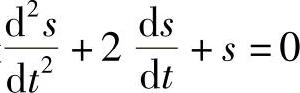 满足初始条件:
满足初始条件: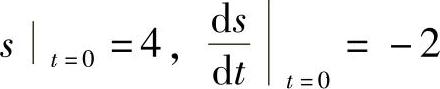 的特解.
的特解.
解 特征方程为r2+2r+1=0,特征根为r1=r2=-1,故方程通解为
s=e-t(C1+C2t).以初始条件st=0=4代入上式,得C1=4,从而
s=e-t(4+C2t).由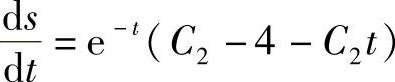 ,
,
将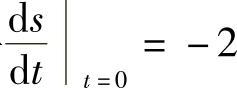 代入上式,得-2=C2-4,有C2=2.
代入上式,得-2=C2-4,有C2=2.
所求特解为s=e-t(4+2t).
3.特征方程有共轭复根r1=α+iβ,r2=α-iβ的情形
容易验证eαxcosβx、eαxsinβx也是齐次微分方程的特解,且它们是线性无关的.
因此齐次微分方程的通解为
y=eαx[C1cosβx+C2sinβx].
例5 求无阻尼自由振动的微分方程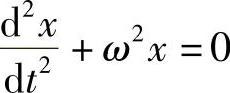 的通解.
的通解.
解 特征方程为r2+ω2=0,它有两个复根r=±iω,故方程的通解为
x=C1cosωt+C2sinωt.
三、二阶常系数线性非齐次微分方程的解法
形如y″+py′+qy=f(x)(f(x)≠0)的方程称为二阶常系数线性非齐次微分方程.
由二阶线性非齐次微分方程解的结构定理知,只要求出它的一个特解和它对应相应的齐次方程的通解即可.
求非齐次方程的一个特解的方法如下.
1)若方程y″+py′+qy=f(x)的右端是f(x)=ϕ(x)eαx的形式,则方程具有形如y∗(x)=xkQ(x)eαx的特解,其中,Q(x)是与ϕ(x)同次的多项式,如果α是对应齐次方程的特征根,则式中的k是α的重数,如果α不是特征根,则k=0.
2)若方程y″+py′+qy=f(x)的右端是f(x)=(Acosβx+Bsinβx)eαx的形式,则方程具有形如y∗(x)=xk(Ecosβx+Fsinβx)eαx的特解,其中,E和F是待定系数,如果α+iβ是对应齐次方程的特征根,则式中的k=1,否则k=0.
例6 求2y″+y′+5y=x2+3x+2的一特解.
解 α=0,不是对应齐次方程的特征根,令方程的特解为
y∗(x)=ax2+bx+c(其中a,b,c是待定系数).
则将y∗′=2ax+b,y∗″=2a,代入原方程,得
4a+(2ax+b)+5(ax2+bx+c)=x2+3x+2,或
5ax2+(2a+5b)x+(4a+b+5c)=x2+3x+2,比较系数得到方程组
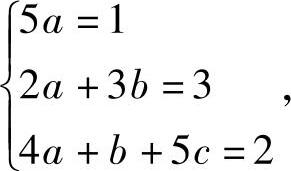
解上面的方程组,得
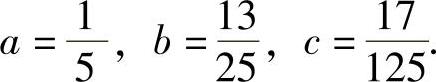
所以方程的特解为
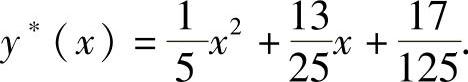
例7 求y″-3y′+2y=xex的通解.
解 与所给方程对应的齐次方程的特征方程为λ2-3λ+2=0,其根为λ1=2,λ2=1,因此对应齐次方程的通解为C1e2x+C2ex.
再求非齐次方程的特解,因α=1是特征方程的一重根,故设特解为
y∗=x(ax+b)ex,将y∗及y∗′,y∗″代入非齐次方程得
-2ax+(2a-b)=x,比较系数得到方程组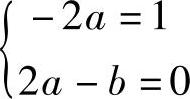 ,解得
,解得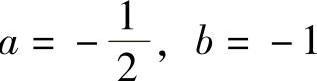 .
.
非齐次方程的特解为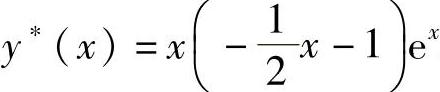 .
.
所以原方程的通解为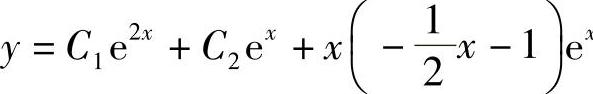 .
.
例8 写出y″+6y′+9y=5e-3x的特解形式和通解形式.
解 特征方程λ2+6λ+9=0的特征根为λ1=λ2=-3.因为α=-3为特征方程的二重根,故特解形式为y∗(x)=Ax2e-3x,通解形式为Y=(C1+C2x)e-3x+Ax2e-3x
例9 求解方程y″+4y=2cos2x的通解.
解 对应齐次方程的特征方程为
λ2+4=0,特征根为λ=±2i,于是对应齐次方程通解为
y=C1cosx+C2sinx.
因为α+iβ=0+2i是特征根,故设特解为y∗=x(acos2x+bsin2x),代入原方程,得
4bcos2x-4asin2x=2cos2x.
比较系数得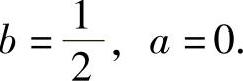 于是
于是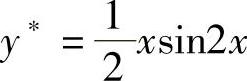
因此原方程的通解为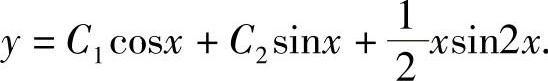
例10 求解方程y″-y=3e2x+2cos2x.
解 由定理6.3,可先将原方程分解为y″-y=3e2x和y″-y=2cos2x,这两个方程的特解为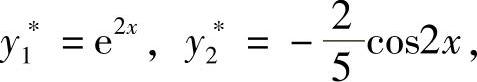
所以所求特解为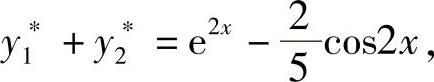
于是所求方程的通解为