几类可降阶的二阶微分方程

第三节 几类可降阶的二阶微分方程

一、y″=f（x）型

如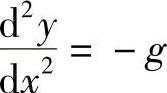属此类型，只要积分两次就可得出通解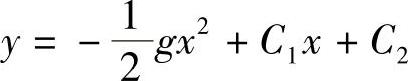，可由初始条件确定这两个任意常数而得到特解.

一般地，对n阶方程

y（n）=f（x），积分n次便可得到通解

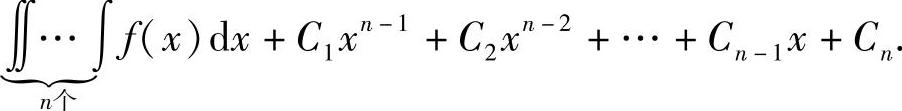
二、y″=f（x，y′）型

特点：方程右端不明显地含未知函数y.

令y′=p（x），则y″=p′（x）代入原方程得

p′（x）=f（x，p（x）），它是关于未知函数p（x）的一阶微分方程.这种方法叫做降阶法.解此一阶方程可求出其通解

p=p（x，C₁）.

由关系式y′=p（x）积分即得原方程的通解为

y=∫p（x，C₁）dx+C₂（C₁，C₂两个任意常数）.

例1 求方程y″-y′=e^x的通解.

解 令y′=p（x），则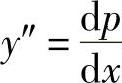，原方程化为.

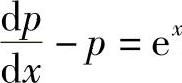这是一阶线性微分方程.由通解公式易得通解

y′=p（x）=e^x（x+C₁）.

故原方程通解为

y=∫e^x（x+C₁）dx

=xe^x-e^x+C₁e^x+C₂

=e^x（x-1+C₁）+C₂.

例2 设有一均匀且柔软的绳索，两端固定，绳索仅受重力的作用而下垂.试问该绳索在平衡状态时是怎样的曲线？

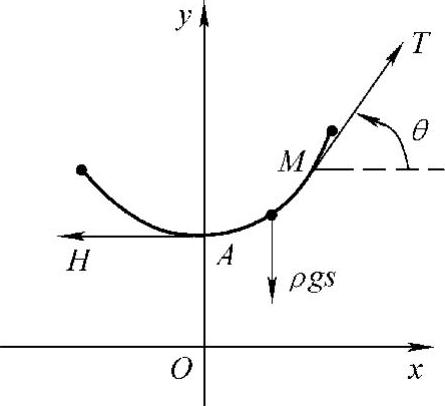
图6-4

解 设绳索的最低点为A.取y轴通过A点铅直向上，并取x轴水平向右，且OA等于某个定值（这个定值将在以后说明）.设绳索曲线的方程为y=φ（x）.考察绳索上点A到另一点M（x，y）间的一段弧，设其长为s.假定绳索的线密度为ρ，则弧所受重力为ρgs.由于绳索是柔软的，因而在点A处的张力沿水平方向的切线方向，其大小设为H；在点M处的张力沿该点处的切线方向，设其倾角为θ，其大小为T（见图6-4）.因作用于弧段的外力相互平衡，把作用于弧上的力沿铅直及水平两方向分解，得

Tsinθ=ρgs，Tcosθ=H.

将此两式相除，得

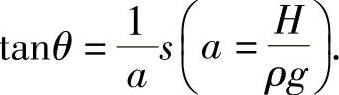
由于

代入上式即得

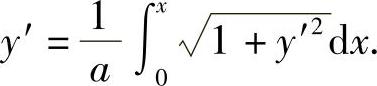
将上式两端对x求导，便得y=φ（x）满足的微分方程

取原点O到点A的距离为定值a，即|OA|=a，那么初始条件为

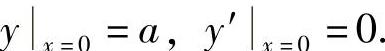
下面来解方程（6-17）.

方程式（6-17）属于y″=f（x，y′）的类型.设y′=p（x），则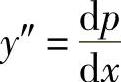，代入方程式（6-17），并分离变量，得

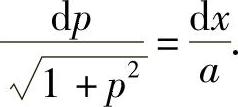
两端积分，得

把条件y′|_x=0=|p_x=0=0代入式（6-18），得

C₁=0，于是式（6-18）成为

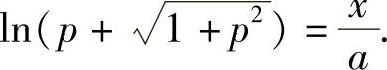
解得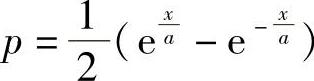，即.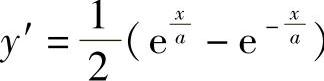

上式两端积分，便得

将条件y|_x=0=a代入式（6-19），得

C₂=0.

于是该绳索的形状可由曲线方程

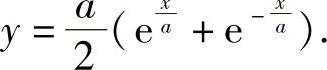
来表示.这曲线叫做悬链线.三、y″=f（y，y′）型

特点：方程右端不明显地含自变量x.

令y′=p（y），则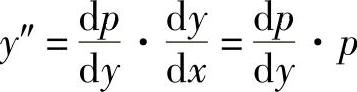，故原方程化为.

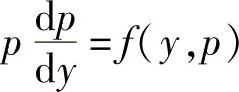这是关于未知函数p（y）的一阶微分方程，设所求出的通解为p=p（y，C₁），即有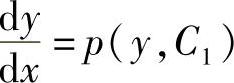，用分离变量法解此方程，可得原方程的通解为y=y（x，C₁，C₂）.

例3 求方程yy″-（y′）2=0的通解.

解 作代换y′=p（y），则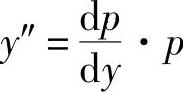，原方程化为

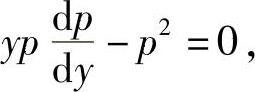
在y≠0、p≠0时，约去p并分离变量有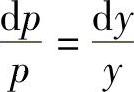，积分得ln|p|=ln|y|+C，所以p=C₁y（C₁=±e^C），即.

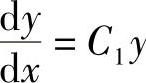再分离变量，求积分得原方程通解为ln|y|=C₁x+C₂′，即

y=C₂e^C1x（C₂=±e^C2′）.