习题6.4

习题6.4

1.验证y₁=cosωx，y₂=sinωx都是微分方程y″+ω²y=0的解，并写出该方程的通解.

2.验证y₁=e^x2，y₂=xe^x2都是微分方程y″-4xy′+（4x²-2）y=0的解，并写出该方程的通解.

3.已知y₁=3，y₂=3+x²，y₃=3+x²+e^x都是微分方程（x²-2x）y″-（x²-2）y′+（2x-2）y=6x-6的解，求该方程的通解.

4.已知y₁=cosx，y₂=sinx都是微分方程y″+y=0的解，y^∗=x²-2是y″+y=x²的解，求y″+y=0的通解.

5.求下列微分方程的通解或在给定条件下的特解：

1）y″-2y′-3y=0；

2）y″+4y′+4y=0；

3）y″+2y′+5y=0；

4）y″+3y′+2y=0，y′|_x=0=1，y|_x=0=1；

5）y″+25y=0，y′|_x=0=5，y|_x=0=2；

6）4y″+4y′+y=0，y′|_x=0=0，y|_x=0=2.

6.求下列微分方程的通解或在给定条件下的特解：

1）y″-5y′+6y=xe^x；

2）y″-2y′-3y=3x+1；

3）y″+y=2x+1；

4）y″-2y′+5y=cos2x；

5）y″+y′-2y=e^-2xsinx.

6）y″-2y′-e^2x=0，y′|_x=0=1，y|_x=0=1.

7.设函数y=y（x）满足y″-3y′+2y=2e^x，且其图像在点（0，1）处的切线与曲线y=x²-x+1在该点的切线重合，求函数y=y（x）.

8.设函数φ（x）连续，且满足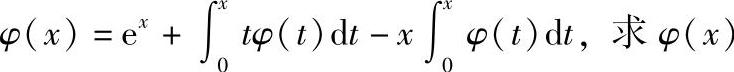.