差分方程简介

第六节 差分方程简介

一、差分与差分方程的一般概念

定义6.3 设函数y=f（x），记为y_x，则差y_x+1-y_x称为y_x的一阶差分，简称为差分，记为Δy_x，即

Δy_x=y_x+1-y^x.

定义6.4 y_x的一阶差分的差分

Δ（Δy_x）=Δ（y_x+1-y_x）=（y_x+2-y_x+1）-（y_x+1-y_x），记为Δ²y_x，称为y_x的二阶差分，即

Δ²y_x=Δ（Δy_x）=y_x+2-2y_x+1+y_x.

同样定义三阶差分，四阶差分，…

Δ³y_x=Δ（Δ²y_x），Δ⁴y_x=Δ（Δ³y_x），…

二阶及二阶以上的差分统称为高阶差分.

由差分的定义，可知差分具有如下性质：

1）ΔC=0（C为常数）；

2）ΔCy_x=CΔy_x（C为常数）；

3）Δ（y_x+z_x）=Δy_x+Δz_x.

例1 求Δ（x²），Δ²（x²），Δ³（x²）.

解 设y_x=x²，那么

Δy_x=Δ（x²）=（x+1）2-x²=2x+1，

Δ²y_x=Δ²（x²）=Δ（2x+1）=[2（x+1）+1]-（2x+1）=2，

Δ³y_x=Δ（Δ²y_x）=Δ（2）=2-2=0.

例2 设y_x=λ^x，求Δy_x.

解 y_x+1=λ^x+1=λ·λ^x=λy_x，于是

Δy_x=y_x+1-y_x=（λ-1）λ_x.

定义6.5 含有自变量、未知函数以及未知函数差分的方程，称为差分方程.方程中含有未知函数差分的最高阶数称为差分方程的阶.

n阶差分方程的一般形式为

F（x，y_x，Δy_x，Δ²y_x，…，Δⁿy_x）=0 （6-25）

将Δy_x=y_x+1-y_x，

Δ²y_x=y_x+2-2y_x+1+y_x，

Δ³y_x=y_x+3-3y_x+2+3y_x+1-y_x，

︙代入式（6-25），则方程变成

F（x，y_x，y_x+1，…，y_x+n）=0 （6-26）

反之，方程式（6-26）也可以化为式（6-25）的形式.因此差分方程也可以定义如下：

定义6.6 含有自变量以及未知函数两个以上（含两个）时期值的符号的方程，称为差分方程.方程中含有未知函数下标的最大值与最小值的差称为差分方程的阶.

比如，二阶差分方程y_x+2-2y_x+1-y_x=3^x，可以化为

y_x^-2yx-1-yx-2=3^x-2.

事实上，将原方程左边写成

（y_x+2-y_x+1）-（y_x+1-y_x）-2y_x=Δy_x+1-Δy_x-2y_x=Δ²y_x-2y_x.

则原方程可以化为Δ²y_x-2y_x=3_x.

定义6.7 如果一个函数代入差分方程后，方程两边恒等，则称此函数为该差分方程的解.

比如，差分方程y_x+1-y_x=2，把函数y_x=15+2x代入此方程，则左边=[15+2（x+1）]-（15+2x）=2=右边，故y_x=15+2x是方程的解.

在实际问题中，往往要根据系统在初始时刻所处的状态，对差分方程附加一定的条件，这种附加条件称之为初始条件.满足初始条件的解称为特解.如果差分方程的解中含有任意常数的，且任意常数的个数恰好等于方程的阶数，则称它为差分方程的通解.

比如，对于一阶差分方程Δy_x=0，易知它的通解是y_x=A（A是任何实常数）.

二、一阶常系数线性差分方程

形如y_x+1+ay_x=f（x）（a≠0，且a为常数） （6-27）的方程称为一阶常系数线性差分方程.

其中，f（x）为已知函数，y_x是未知函数.解差分方程就是求出方程中的未知函数.式（6-27）中当f（x）≠0时，称之为非齐次的，否则称之为齐次的.即

y_x+1+ay_x=0 （6-28）该式称为与式（6-27）对应的齐次差分方程.

下面介绍一阶常系数差分方程的解法

1.齐次方程的解

显然，y_x=0是方程式（6-28）的解.

若y_x≠0，则有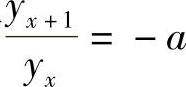，即{y_x}是以A为首项，公比为-a的等比数列，于是方程式（6-28）的通解为y_x=Aa^x.当a=1时，通解为y_x=A.

2.非齐次方程的解法

由前面的概念可以看出，差分方程与微分方程有许多相似之处.微分方程描述变量连续变化过程，而差分方程一般描述变量离散变化过程.当自变量间隔很小时，差分可以看成微分的近似.因此，差分方程和微分方程在解的结构、解的性质以及求解方法上基本相似.比如，若y_x^∗是式（6-27）的一个特解，Y_x是式（6-28）的解，则y_x=y_x^∗+Y_x是式（6-27）的解.事实上，

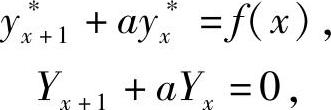
两式相加得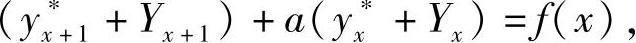即y_x=y_x^∗+Y_x是式（6-27）的解.

因此，如果y_x^∗是式（6-27）的一个特解，则

y_x=y_x^∗+Aa^x

就是式（6-27）的通解.这样，为求式（6-27）的通解，只需求出它的一个特解即可.

下面来讨论当f（x）是某些特殊形式的函数时式（6-27）的特解.

情形1 f（x）=p_n（x）（n次多项式），则方程式（6-27）为

y_x+1+ay_x=p_n（x），（6-29）

如果y_x是m次多项式，则y_x+1也是m次多项式，并且当a≠-1时，y_x+1+ay_x仍是m次多项式，因此若y_x是式（6-29）的解，应有m=n.

于是，当a≠-1时，设y_x^∗=B₀+B₁x+…+B_nxⁿ是式（6-29）的特解，将其代入式（6-29），比较两端同次项的系数，确定出B₀，B₁，…，B_n，便得到式（6-29）的特解.

当a=-1时，方程式（6-29）成为y_x+1-y_x=p_n（x），或Δy_x=p_n（x）.因此，y_x应是n+1次多项式，此时设特解为y_x^∗=x（B₀+B₁x+…+B_nxⁿ），代入式（6-27），比较两端同次项系数来确定B₀，B₁，…，B_n，从而可得特解.

特别地，p_n（x）=C（C为常数），则式（6-29）为

y_x+1+ay_x=C （6-30）

当a≠-1时，设y_x^∗=k，代入式（6-30）得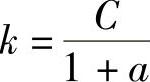，所以特解为.

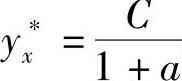当a=-1时，设y_x^∗=kx，代入式（6-30），得k=C，得特解为y_x^∗=Cx.

例3 求差分方程y_x+1-3y_x=-2的通解.

解 a=-3≠1，C=-2，对应齐次方程的通解为Y=A3^x.非齐次方程的特解为

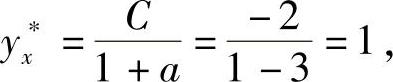
所以，差分方程的通解为y_x=1+A3_x.

例4 求差分方程y_x+1-2y_x=3x²的通解.

解 由a=-2知，对应齐次方程的通解为Y=A2^x.

设y_x=B₀+B₁x+B₂x²是方程的解，将它代入方程，则有

B₀+B₁（x+1）+B₂（x+1）2-2B₀-2B₁x-2B₂x²=3x²，整理得（-B₀+B₁+B₂）+（-B₁+2B₂）x-B₂x²=3x²，比较同次项系数得

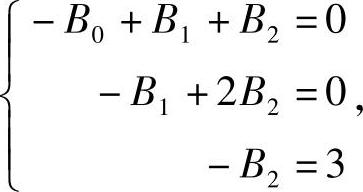
解得B₀=-9，B₁=-6，B₂=-3，方程的特解为y_x=-9-6x-3x²，而相应的齐次方程的通解为A2^x，于是得差分方程的通解y_x=-9-6x-3x²+A2^x.

例5 求差分方程y_x+1-y_x=3x²+x+4的通解.

解 由a=-1知，对应齐次方程的通解为Y=A.

设特解为y_x^∗=x（B₀+B₁x+B₂x²），代入原方程得

3B₂x²+（2B₁+3B₂）x+（B₀+B₁+B₂）=3x²+x+4，

比较系数得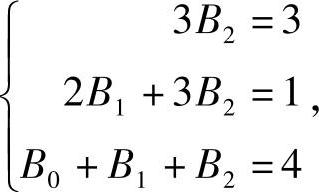

解得B₀=4，B₁=-1，B₂=1，

特解为y_x^∗=x（4-x+x²）.

因而得通解y_x=x³-x²+4x+A.

情形2 f（x）=cb^x（其中c、b均为常数，且b≠1），即

y_x+1+ay_x=cb^x.（6-31）

当b≠-a时，设y_x^∗=kb^x为特解，代入式（6-31）并化简，得k（b+a）=c，所以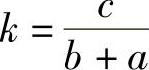，于是.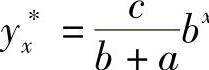

当b=-a时，设y_x^∗=kxb^x为特解，代入式（6-31）并化简，得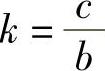，所以特解为.

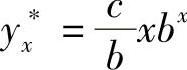例6 求差分方程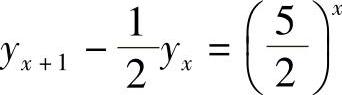的通解.

解 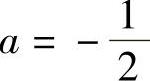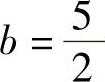，，c=1，对应齐次差分方程的通解为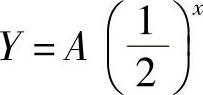，非齐次差分方程的特解为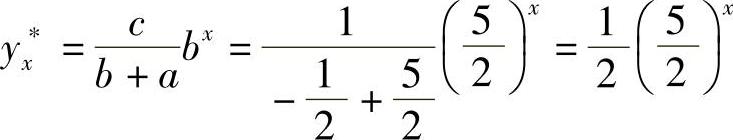，所以，原差分方程的通解为

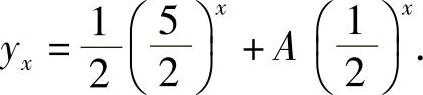
例7 求差分方程y_x+1-2y_x=3·2^x满足初始条件y₀=4的特解.

解 由a=-2知，对应齐次差分方程的通解为Y=A·2^x.由于b=2=-a，则特解为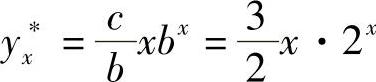，所以原方程的通解为.

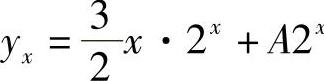代入初始条件y₀=4，解得A=4，所以原方程的特解为

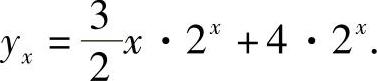
三、二阶常系数线性差分方程

形如

y_x+2+ay_x+1+by_x=f（x） （6-32）的方程称为二阶常系数线性非齐次差分方程.

当f（x）≡0时，式（6-32）变为

y_x+2+ay_x+1+by_x=0 （6-33）称为二阶常系数线性齐次差分方程.

1.二阶常系数线性差分方程解的结构

定理6.5 设y_1x与y_2x都是式（6-33）的解，则y_1x与y_2x的线性组合

y_x=A₁y_1x+A₂y_2x也是式（6-33）的解.

定理6.6 设y_1x与y_2x都是式（6-33）的解，且y_1x与y_2x线性无关，则

y_x=A₁y_1x+A₂y_2x便是式（6-33）的通解，其中A₁，A₂是任意常数.

定理6.7 设y_x=A₁y_1x+A₂y_2x是式（6-33）的通解，且y_x^∗是式（6-32）的一个特解，则

Y=y_x^∗+A₁y_1x+A₂y_2x是式（6-32）的通解.

由上面的定理，为了求出方程式（6-32）的通解，只需先求出相应的齐次方程（6-33）的两个线性无关的通解，再求出式（6-32）的一个特解即可.

2.二阶常系数线性齐次差分方程的解

与相应的二阶微分方程类似，可设方程式（6-33）具有形如y_x=λ^x的特解，代入式（6-33）并消去λ^x，得

λ²+aλ+b=0 （6-34）

式（6-34）称为式（6-33）的特征方程.根据方程式（6-34）的根的不同情况，讨论如下.

1）设特征方程式（6-34）有两个不同的实根λ₁≠λ₂，则式（6-33）有两个线性无关的特解y_1x=λ^x₁，y²_x=λ^x₂.

因此式（6-33）的通解便是y_x=A₁λ^x₁+A₂λ^x₂.

2）设特征方程式（6-34）有两个相同的实根λ₁=λ₂=λ，则y_1x=λ^x是式（6-33）的一个特解.仿微分方程可求出另一特解

y_2x=xλ_x.于是式（6-33）的通解是

y_x=（A₁x+A₂）λ^x（A₁，A₂是任意常数）.

3）设式（6-33）的特征方程式（6-34）有两个共轭的复数根

λ₁=α+βi，λ₂=α-βi.

可以证明方程方程式（6-33）有两个线性无关的实数特解

y₁^∗=r^xcosβx，y₂^∗=r^xsinβx.其中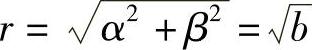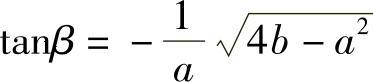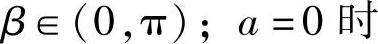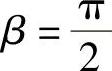，，，，因此式（6-33）的通解是y_x=r^x（A₁cosβx+A₂sinβx）.

例8 假设有人年初买了一对小兔子，经一个月生长，长成了大兔子，便开始繁殖，且每月都生一对小兔子，而小兔子又遵循年初那对兔子的繁殖规律，问第x个月兔子有多少对（假设兔子都不死亡）？

解 设第x个月兔子的对数是y_x，则第x+2个月的兔子数目可以这样得到：

第x+1个月的兔子在第x+2个月依然存在，但它们有大有小不一定都生小兔子，而第x个月的所有兔子到第x+2个月都生一对兔子，因此有y_x+2=y_x+1+y_x，即y_x+2^-yx+1-yx=0，且y₀=y₁=1.

特征方程是λ²-λ-1=0.

求得两个根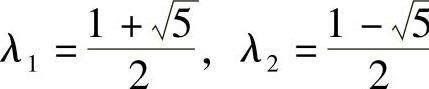.于是原问题的解是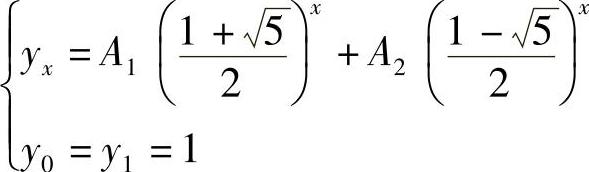，确定A₁，A₂之后，便得.

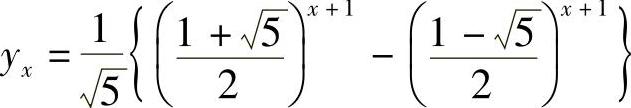3.二阶常系数线性非齐次方程的解法

与一阶非齐次差分方程类似，二阶非齐次差分方程的特解同样可以采用待定系数法求.非齐次方程特解类型与方程右端项f（x）有关，具体参见表6-1。

表6-1

（续）

例9 求差分方程y_x+2+y_x+1-2y_x=12的通解及y₀=y₁=0时的特解.

解 相应齐次方程y_x+2+y_x+1-2y_x=0的特征方程为

λ²+λ-2=0，解得特征根为λ₁=-2，λ₂=1，于是齐次方程的通解是

y_x=A₁（-2）x+A₂.

由于a+b+1=0，且a=1≠-2，故设原方程的一个特解是

y_x^∗=a₀x，代入原方程，得a₀=4，因此，特解是

y_x^∗=4x.

于是，原方程的通解为Y=A₁（-2）x+A₂+4x.

由y₀=0，y₁=0得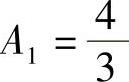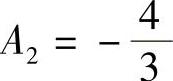，.故所求特解为.

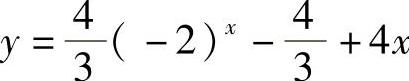例10 求差分方程y_x+2+5y_x+1+4y_x=x的通解.

解 对应齐次方程的特征方程是λ²+5λ+4=0，

特征根为λ₁=-1，λ₂=-4，

齐次方程的通解y_x=A₁（-1）x+A₂（-4）x.

由于a+b+1=10≠0，故设y_x^∗=ax+b为非齐次方程的一个特解，代入原方

程得

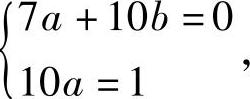
解得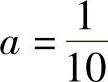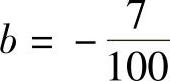，，于是.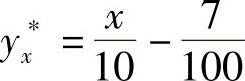

原方程的通解为

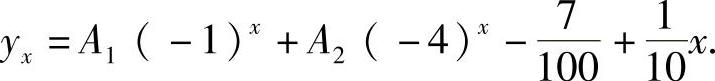
例11 求差分方程y_x+2-10y_x+1+25y_x=3^x的通解.

解 对应齐次方程的特征方程是

λ²_-10λ+25=0，

解得特征根为λ₁=λ₂=5，

于是齐次方程通解是y_x=（c₁+c₂x）·5^x.

又因为d=3不是特征根，故可设非齐次特解是y_x^∗=A·3^x，代入原方程求得.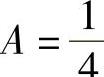

故原方程的通解为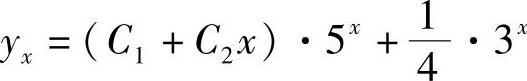.