习题5.4

习题5.4

1.计算下列曲线所围成的平面图形的面积：

1)y=x²,y=x;2)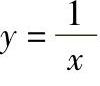，y=x，x=2；3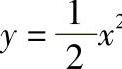）2，y=x+4；4）y=e^x，y=e^-x，x=1；5）y=x²-x，y=1-x²；6）y=x²，4y=x²，y=1.

2.求曲线y=x³-3x+2在x轴上介于两极值点间的曲边梯形的面积.

3.求c（c＞0）的值，使两曲线y=x²与y=cx³所围成的图形的面积为.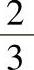

4.求位于曲线y=e^x下方，该曲线过原点的切线的左方及x轴上方之间的图形的面积.

5.求下列平面图形分别绕x轴、y轴旋转所得的旋转体的体积：

1）曲线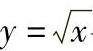与直线x=1，x=4，y=0所围成的图形；2）在区间[0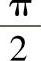，]上，曲线y=sinx与直线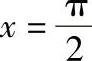，y=0所围成的图形；3）曲线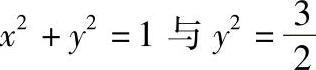x所围成的两个图形中较小的一块.

6.求圆盘x²+y²≤a²绕直线x=-b（b＞a＞0）旋转所成的旋转体的体积.

7.计算曲线y=lnx上对应于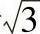≤x≤8的一段弧的长度.

8.计算半立方抛物线y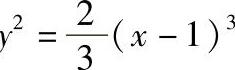被抛物线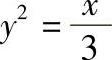截得的一段弧的长度.

9.计算星形线x=acos³t，y=asin³t的全长（见图5-17）.

10.在摆线x=a（t-sint），y=a（1-cost）上求分摆线第一拱成1∶3的点的坐标.

11.求曲线ρθ=1上对应于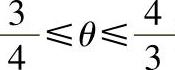的一段弧的长度.

12.求心形线ρ=a（1+cosθ）的全长.

13.把一个带+q电量的点电荷放在r轴上坐标原点O处，它产生一个电场.这个电场对周围的电荷有作用力.由物理学知道，如果有一个单位正电荷放在这个电场中距离原点O为r的地方，那么电场对它的作用力的大小为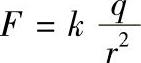（k是常数）.当这个单位正电荷在电场中从r=a处沿r轴移动到r=b（a＜b）处时，计算电场力F对它所做的功.

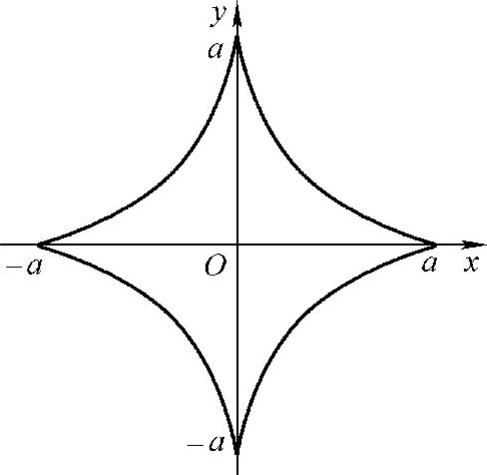
图5-17

14.一圆柱形的贮水桶高为5m，底圆半径为3m，桶内盛满了水.试问要把桶内的水全部吸出需做多少功？

15.一个横放着的圆柱形水桶，桶内盛有半桶水.设桶的底半径为R，水的比重为ρ，计算桶的一个端面上所受的压力.

16.设有一半径为R，中心角为φ的圆弧形细棒，其线密度为常数ρ，在圆心处有一质量为m的质点M，试求这细棒对质点M的引力.

17.已知某产品总产量的变化率是时间t（单位：年）的函数

f（t）=2t+5（t≥0），

求第一个五年和第二个五年的总产量各为多少？

18.已知某产品生产x个单位时，总收益R的变化率（边际收益）为(x≥0)，

1）求生产了50个单位时的总收益；

2）如果已经生产了100个单位，求再生产100个单位时的总收益.

19.已知某产品的边际收入函数为R′（x）=25-2x（x≥0），

边际成本函数为C′（x）=13-4x（x≥0），

固定成本C₀=10，求当x=5时的毛利润和纯利润.

20.假设某产品的边际收入函数为R′（x）=9-x（x≥0），

边际成本函数为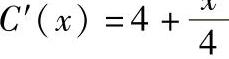(x≥0)（万元/万台），

1）试求当产量由4（万台）增加到5（万台）时利润的变化量；

2）当产量x为多少时利润最大？

3）已知固定成本为1（万元），求总成本函数C（x）和利润函数L（x）.