6.2.2 负斜率的股票需求曲线理论模型
Wurgler和Zhuravskaya（2002）提出了有限替代模型。该模型假定有两类投资者：套利者与非套利者。两者主要区别：一是套利者对资产价值有正确和同质信念；二是套利者受到零净投资约束。总需求曲线由套利者与非套利者的需求曲线进行水平加总得到。
考虑一个市场有n项风险资产，在t=0期买入，在t=1期卖出。收益是
满足正态分布。因为某些原因，如一个外生冲击，资产j发生了错误定价，当其他资产的预期收益是0的时候，它的预期收益
套利者将因为错误定价而进入市场。
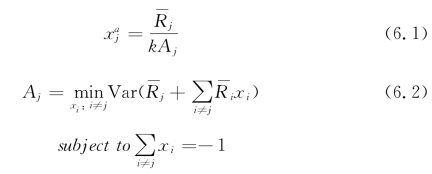
其中，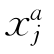
表示对资产j的超额需求，
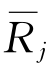表示预期收益且不等于0，k表示不变绝对风险厌恶系数，Aj表示资产j的套利风险，由投资组合方差最小值衡量。
表示卖出＄1空头资产i，从而买入＄1多头资产j构成的一个零投资组合。
记
那么
结合式（6.1）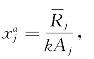
可以得到式（6.3）：
因此，在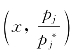
空间里，套利者超额需求曲线截距为1，斜率为-kAj。
如果套利者风险厌恶为0（k=0）或资产具有完全替代（A=0），则需求曲线无穷弹性并且完全平坦。
非套利投资者超额需求为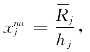
相应的，其股票需求曲线为式（6.4）：
其中，hj是非套利投资者关于股票真实价格认识的异质程度度量指标。如果投资者关于股票真实价值认识是同质的，即hj等于0，则价格不随需求量改变，股票需求弹性无穷大；否则，股票需求曲线是有限的。
对两类投资者股票需求曲线加总，即可得到总需求曲线为式（6.5）：
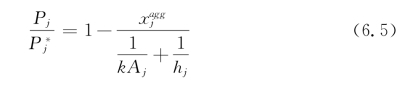
其中，
考虑到金融市场存在N个同质套利者，则总需求曲线为式（6.6）：
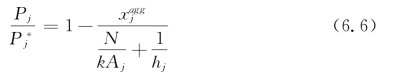
从式（6.6）可以看出来，股票需求曲线斜率取决于四个变量：股票的可替代性Aj、套利者数量N、套利者风险厌恶系数k和非套利投资者对股票真实价值认识的异质度hj。其与斜率的关系：①股票的可替代性越大，Aj值越小，斜率就越小；②套利者数量N越大，斜率越小；③套利者风险厌恶系数k越小，斜率越小；④非套利投资者对股票真实价值认识的差异程度hj越低，斜率越小。
由于有限替代模型的假设具有一般性，所以该模型在任何市场都在一定程度上成立。
除此之外，Petajisto（2007）在新古典金融理论框架内对CAPM进行改进，建立了一个新的模型，其基本思路是：在市场参与者结构中，除代表性投资者和噪声交易者外，引入积极基金管理人（以下简称积极经理），系统性风险定价仍然由代表性投资者决定，而横截面个股价格则由积极经理决定。但是由于中国的机构投资者起步较晚，公募基金的资金规模相对较小，这一模型对于A股股票市场的适用性非常有限，这里就不做详细介绍。
Ofek和Richardson（2002）的模型从异质信念的角度，对股票需求曲线进行理论研究，我们认为其对A股市场有着较强的解释能力。异质信念通常是指不同投资者对相同股票在相同持有期下的期望收益率或者期望收益率方差的估计不同。这虽然是一个比较直观的现象，但在理论与实证分析中，仍需要对异质信念的形成机制进行规范性描述。标准资产定价理论的一致性预期假设暗含两个前提：一是所有信息对所有投资者免费并且同时到达；二是所有投资者处理信息的方式（先验信念）相同。这两个条件不成立就形成了投资者之间异质信念的假设，Hong和Stein（2007）从这个角度出发总结了异质信念形成的三种渠道：渐进信息流（gradual information flow）[2]（Hong and Stein，1999）、有限注意（limited attention）[3]（Hirshleifer and Teoh，2003）与先验的异质性（heterogeneous priors）[4]（Kandel and Pearson，1995）。
异质信念对股票收益影响的理论研究最早开始于Milier（1977），他认为，在异质信念和卖空限制的前提下，投资者对未来的不同预期将会影响股票价格的均衡，对未来持乐观态度的投资者将会买入和持有股票，而悲观的投资者却因为卖空限制而不能充分表达和参与市场交易，其结果是股票价格主要反映了乐观投资者的意见，造成了股票价格相对于其真实价格的高估。投资者意见分歧的程度越大，该股票被高估的程度就越高；同样，越受到卖空的限制，股票被高估的程度越严重。随着时间的推移，信息传递逐渐充分，投资者意见逐渐趋向于一致时，价格会趋向于真实价值。除了Milier之外，Jarrow（1980），Figlewski（1981），Chen，Hong和Stein（2000）也分别提出不同的模型说明理性的投资者存在卖空限制的情况下，他们只有离开市场。Jones和Lamont（2001）指出，当存在足够多的非理性交易者时，股价将会被高估。Lamont和Thaler（2000），Mitchell等（2001）也从错误定价和套利的角度提出了相似观点。Detemple和Murthy（1997），Basak和Croitoru（2000）分别提出了动态模型，投资者对于资产的异质信念将会导致资产价格偏离均衡状态。
Ofek和Richardson（2002）在Lintner（1969）模型的基础上，提出了一个异质信念代表性模型。其模型假设：投资者对于股票资产的收益有着异质信念，所以股票价格是不同信念投资者的观点的综合反映；最悲观的投资者由于卖空限制，他们的观点不能反映到股票价格中去。假设这里有M个投资者，每个人都有参数为αj风险厌恶的效用函数，但是对资产收益有着不同的预期分布。对于N种资产的预期收益分布为一个均值μj和方差协方差为Ωj的矩阵。假设无风险资产为固定利率r0，P0=1。进一步假设固定数量的风险资产分别被M个投资者所持有。
每个投资者对于风险资产的需求可以表示如式（6.7）：
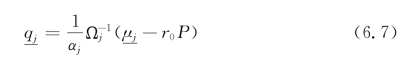
式中，下划线表示向量。q表示需求，P表示资产的价格。加总所有的个人需求，使得供求平衡时候的资产价格为式（6.8）：
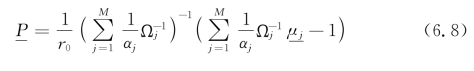
在式（6.8）中，价格是对资产收益的平均信念的表达，权重取决于投资者的风险厌恶系数和支付的方差协方差矩阵。直觉上，风险更加厌恶的投资者有越高的风险厌恶系数αj或者在方差协方差矩阵|Ωj|，他们的信念在资产价格的形成中所占权重就越小。除此之外，当然一个投资者所持资产越多，他的信念也会更大程度影响价格。把（6.8）式代入（6.7）式，可以得出每个投资者的最优持有风险资产头寸如式（6.9）。
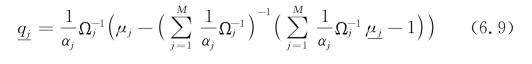
从式（6.9）我们可以得出几点结论：如果投资者有着相同的信念，式（6.9）可以简化为CAPM公式如下：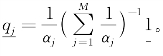
这就是说，每个投资者持有的市场份额，取决于他对风险的偏好。
从式（6.9）看出，当投资者的信念发生分歧的时候，如果某个投资者对某项资产n的μj非常低，那么该投资者会卖出资产n，而其他投资者就应该持有更多的该资产。
这个模型可以用来讨论卖空限制，qj必须大于-q*，-q*表示任何一个投资者所能卖空的头寸。如果完全不能卖空，那么q*就应该等于0。
当一个悲观的投资者想卖出超过q*的股票时，由于卖空限制，只能卖q*或者更少，这样一来，他们的信念就不能完全反映到资产价格中去，市场均衡价格对于乐观投资者给予了更多的权重，考虑到一个极端情况是，悲观投资者全部离开市场，不再拥有股票，那么股票价格将仅仅反映乐观投资者的信念，悲观投资者本来可以卖空股票，平抑市场价格，但是由于卖空限制而被禁止。
卖空约束，我们可以理解为对股票供给的限制，卖空约束的解除，我们可以理解为股票供给的增多，Ofek和Richardson模型告诉我们，随着卖空的解除，市场将从反映乐观投资者的信念逐渐向悲观投资者信念的天平倾斜，在这一过程中，股价将会出现下移，这将表明，股票供给数量的增加将对股价产生向下的压力，说明股票的需求曲线是倾斜的。
数量型的金融约束政策则对股权进行分置，保持一部分限售股不流通，实质上就是一种卖空限制，由于限售股持有者主要是产业投资者，他们对上市公司有着更多的了解，比一般投资者更加理性和全面，在限售股解禁之前，由于所持股份一直处于限售状态，即对他们而言，存在着卖空限制，那么实际上，在股票没有全流通之前，市场均衡价格只是反映了流通股股东的信念，在限售股解禁之后，非流通股股东的信念也将能反映在股价上面，非流通股股东的悲观信念将会得到表达，那么股价下跌将不可避免。