误差的分类及其特点
按误差产生的原因和性质的不同,可分为系统误差、随机误差和粗大误差。
1.系统误差
系统误差指误差值的大小和正负总保持不变,或按一定的规律变化,或是有规律的重复。系统误差有多种来源,从物理实验教学角度出发,主要有:
(1)仪器的零值误差。例如电表的指针不指在0位,即产生零值误差。所以在使用电表前,应先检查指针是否指0,否则须旋动零位调节器使指针指0。又如,在使用千分尺测长度之前,也要先检查0位,并记下零值读数(即零值误差),以便对测量值进行修正。
(2)仪器机构误差和测量附件误差等。如果天平的两个臂不完全相等,将被测物体与砝码交换,两次测量结果分别为m1、m2,则被测物体质量![]() ;如电学线路中电表内阻、导线电阻、接触电阻等电阻所引入的误差,有时可用替代法和示零法(电位差计、电桥)来巧妙地避免这些因素的影响。
;如电学线路中电表内阻、导线电阻、接触电阻等电阻所引入的误差,有时可用替代法和示零法(电位差计、电桥)来巧妙地避免这些因素的影响。
(3)理论和方法误差。由于实验理论和实验方法不完善,所引用的理论与实验条件不符等产生的误差。如用伏安法测未知电阻,由于电表内阻的影响,使测量值比实际值总是偏大或总是偏小;单摆周期公式![]() 的成立条件是摆角小于5°,用此公式测量重力加速度本身带来的误差。
的成立条件是摆角小于5°,用此公式测量重力加速度本身带来的误差。
(4)测量环境变化和操作人员心理、习惯等因素造成误差。前者由于周围温度、气压、振动、电磁场等环境变化发生有规律变化引起误差;后者由测量人员测量习惯不科学引起有规律变大或变小。如测量长度斜视等。
系统误差也包括按一定规律(指非统计规律)变化的误差。如“分光计的使用和调整”实验中角度的测量存在周期性的误差,此误差可通过对称设置双读数游标来解决。在“霍尔效应及磁场测量”实验中,通过改变工作电流和励磁电流(产生磁场)方向加以消除霍尔电压测量系统误差。
从上述的介绍可知,我们不能依靠在相同条件下多次重复测量来发现系统误差的存在,也不能借此来消除它的影响。原则上,系统误差均应予以改正,但系统误差的发现和估计,是个实验技能问题,常取决于实验者的经验和判断能力。在物理实验教学中,处理系统误差的通常做法是:首先,对实验依据的原理、方法、测量步骤和所用仪器等可能引起误差的因素一一进行分析,查出系统误差源;其次,通过改进实验方法、实验装置、校准仪器等方法对系统误差加以补偿、抵消;最后,在数据处理中对测量结果进行理论上修正,以消除或尽可能减小系统误差对实验结果的影响。
2.随机误差
(1)正态分布函数及标准误差。随机误差是指在多次等精度测量中,误差变化是随机的(包括大小和正负),没有规律,而测量次数很多时满足统计规律的误差。
随机误差是由实验中各种因素的微小变动性引起的,测量对象的自身涨落,测量仪器指示数值的变动性,以及观测者本人在判断和估计读数上的变动性等。这些因素的共同影响就使测量值围绕着测量的平均值发生有涨落的变化,这变化量就是各次测量的随机误差。
虽然某一测量值的随机误差是没有规律的,其大小和方向都是不可能预知的。但对某一量进行足够多次的测量,则会发现其随机误差服从一定的统计规律分布,即高斯分布,又称正态分布。分布函数为
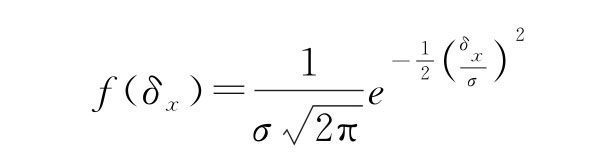
且满足概率
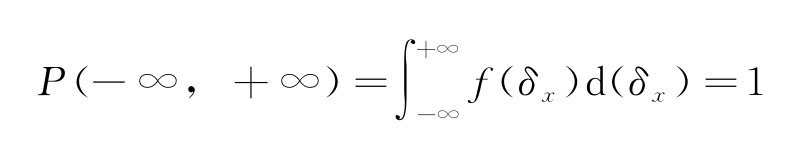
式中σ 称标准误差,是随机误差δx的分布函数f(δx)的特征量,是一个与测量条件有关的常量。它的大小反映测量的数据离散程度大小,数值越小,测量的数据越密集,精密度越高。其表达式为
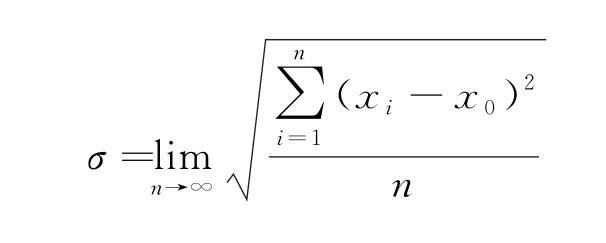
随机误差δx的分布函数f(δx),如图1-1所示。
正态分布函数四个重要特点:(https://www.daowen.com)
1)单峰性:测量值与真值相差越小,这种测量值(或误差)出现的概率(可能性)越大,与真值相差大的,则概率越小。
2)对称性:绝对值相等、符号相反的正、负误差出现的概率相等。
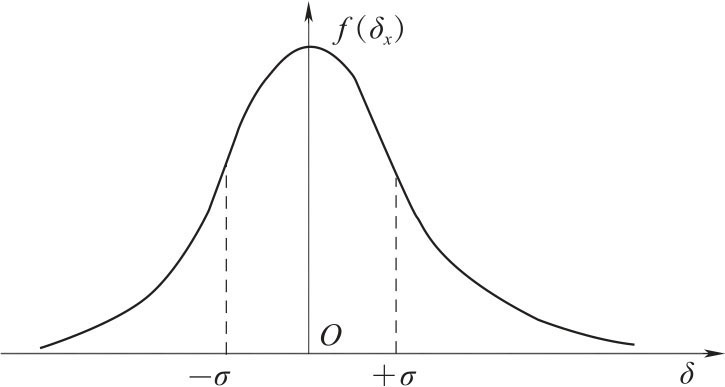
图1-1 正态分布随机误差函数图
3)有界性:绝对值很大的误差出现的概率趋近于零。也即是说,总可以找到这样一个误差限,某次测量的误差超过此限值的概率小到可以忽略不计的地步。
4)抵偿性:随机误差的算术平均值随测量次数的增加而减小。
随机误差曲线f(δx)在区间d(δx)的面积f(δx)d(δx)表示在区间d(δx)的概率,随机误差在相应区间的概率值:
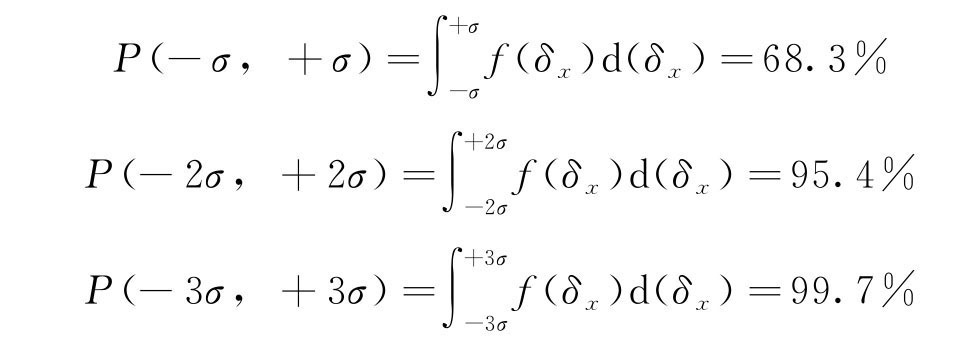
这说明对任一次测量,其测量值误差出现在区间(-σ,σ)内的概率为68.3%。标准误差只是一个统计性质的特征量。表示测量值离散程度。测量值误差出现在区间(-3σ,3σ)外的概率很小,只有0.3%。也就是说,每1000次测量,有3次测量的绝对误差值会超过3σ。实际测量最多几十次,因此测量的绝对误差值超过3σ 范围情况几乎不为出现,所以称3σ 为极限误差。
由于误差存在,真值实际上无法测得。根据误差函数对称性,有
由算术平均值定义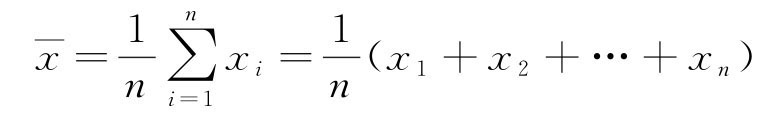
则
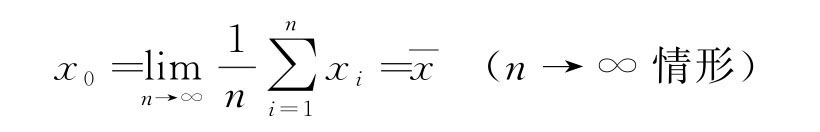
实际测量次数有限,从而算术平均值最接近真值,是真值最佳估计值。
(2)算术平均值标准误差。对某一物理量进行等精度多次重复测量,将测得数据分成几组,每组数据个数相同。由于随机误差影响,每组数据算术平均值可能不同,因此测量列算术平均值本身存在离散性。引入算术平均值标准误差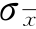 ,可以证明
,可以证明
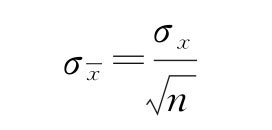
算术平均值标准误差表示算术平均值误差![]() 在区间
在区间 ![]() 之内概率为68.3%,或者说真值在
之内概率为68.3%,或者说真值在![]() 范围内概率为68.3%。
范围内概率为68.3%。
(3)测量列标准偏差。标准误差σ 只有在理论上的意义,当n→∞时,才趋于正态分布。在实际测量中,真值无法测得,测量次数有限,随机误差不符合正态分布,而遵从t 分布(又称学生分布),通常用算术平均值参与标准误差估算,实验中用贝塞尔公式计算测量列x1,x2,…,xn标准偏差Sx。
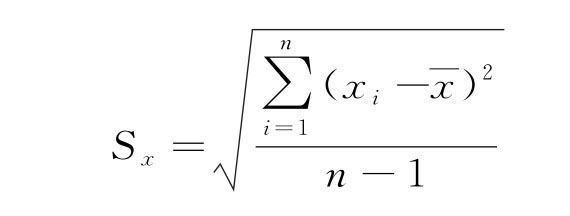
![]() 称测量列偏差,用Δxi表示,
称测量列偏差,用Δxi表示,![]() (i=1,2,…,n)。
(i=1,2,…,n)。
当测量次数n→∞时,则 →x0,Sx→σx,也就是说无限多次重复测量算术平均值最接近真值,标准偏差最接近标准误差。实际测量时用Sx估算σx值。
→x0,Sx→σx,也就是说无限多次重复测量算术平均值最接近真值,标准偏差最接近标准误差。实际测量时用Sx估算σx值。
标准偏差可以表示这一列测量值的精密度,反映出测量值的离散性。标准偏差小就表示测量值很密集,即测量的精密度高;标准偏差大就表示测量值很分散,即测量精密度低。现在很多计算器上都有这种统计计算功能,可以直接用计算器求得Sx和 等数值。
等数值。
(4)测量列算术平均值标准偏差。由于随机误差影响,同样测量列算术平均值也存在离散性。测量列算术平均值标准偏差用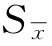 表示。可以证明
表示。可以证明
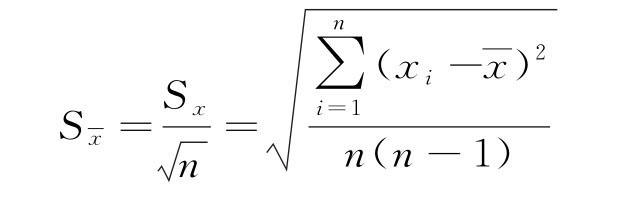
所以用算术平均值标准偏差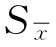 估计算术平均值标准误差
估计算术平均值标准误差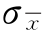 的值。
的值。
3.粗大误差
明显超出规定条件下预期值的误差称为粗大误差,例如|σx|>3σ。这是在实验过程中,由于某种差错使得测量值明显偏离正常测量结果的误差。例如读错数、记错数或者环境条件突然化而引起测量值的错误等。在实验数据处理中,将某次测量误差|σx|>3σ 的粗大误差应剔除。
