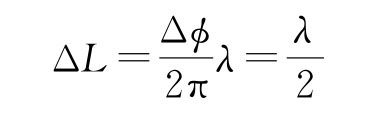【实验原理】
由波动理论得知，声波的传播速度v 与声波频率f 和波长λ 之间的关系为v=fλ。所以只要测出声波的频率和波长，就可以求出声速。其中声波频率可由产生声波的电信号发生器的振荡频率读出，波长则可用共振法和相位比较法进行测量。
1.压电陶瓷换能器
实验采用压电陶瓷换能器来实现声压与电压之间的转换。它主要由压电陶瓷片、轻金属铅（做成喇叭形状，增加辐射面积）和重金属（如铁）组成，如图2-18所示。压电陶瓷片由多晶体结构的压电材料锆钛酸铅制成。超声波的产生是利用压电陶瓷的逆压电效应，在交变电压作用下，压电陶瓷纵向长度周期性地伸、缩，产生机械振动而在空气中激发出超声波。超声波的接收是利用压电陶瓷的正压电效应使声压变化转变为电压的变化。压电陶瓷换能器在声-电转化过程中信号频率保持不变。
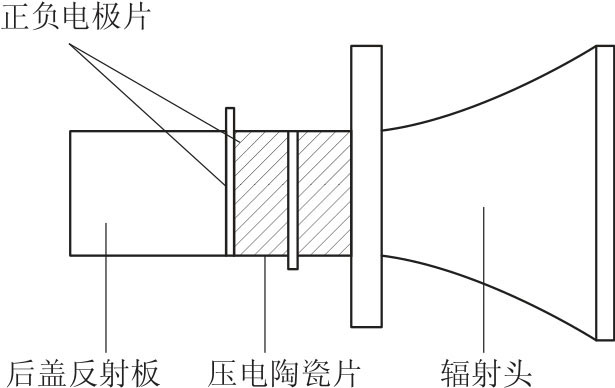
图2-18 压电陶瓷换能器结构
压电换能器系统有其固有的谐振频率f0，当输入电信号的频率等于谐振频率时，它的振幅最大，作为波源其辐射功率就最大；当外加强迫力以谐振频率迫使压电换能器产生机械谐振时，它作为接收器转换的电信号最强，即灵敏度最高。
本实验中，压电换能器的谐振频率在35～39kHz范围内，相应的超声波波长约为1cm。由于波长短，而发射器端面直径比波长大得多，因而定向发射性能好，离发射器端面稍远处的声波可以近似认为是平面波。
2.测量声速的实验方法
声波的传播速度v 可以由声波频率f 和波长λ 求出
v=fλ
其中声波频率可由信号发生器的显示屏读出，实验中的主要任务就是测声波波长。
（1）共振干涉法（驻波法）测量波长λ。按照波动理论，发射器发出的平面声波经介质到接收器，若接收面与发射面平行，声波在接收面处就会被垂直反射，于是平面声波在两端面间来回反射并叠加。如图2-19所示，发射换能器S1发出一平面波超声波，接收换能器S2把接收到的超声波的声压转换成交变的正弦电压信号后输入示波器观察。S2在接收超声波的同时还反射一部分超声波。这样，由S1发出的超声波和由S2反射的超声波在S1和S2之间形成驻波，产生定域干涉。如果S1和S2之间的距离L 恰好等于半波长的整数倍，即
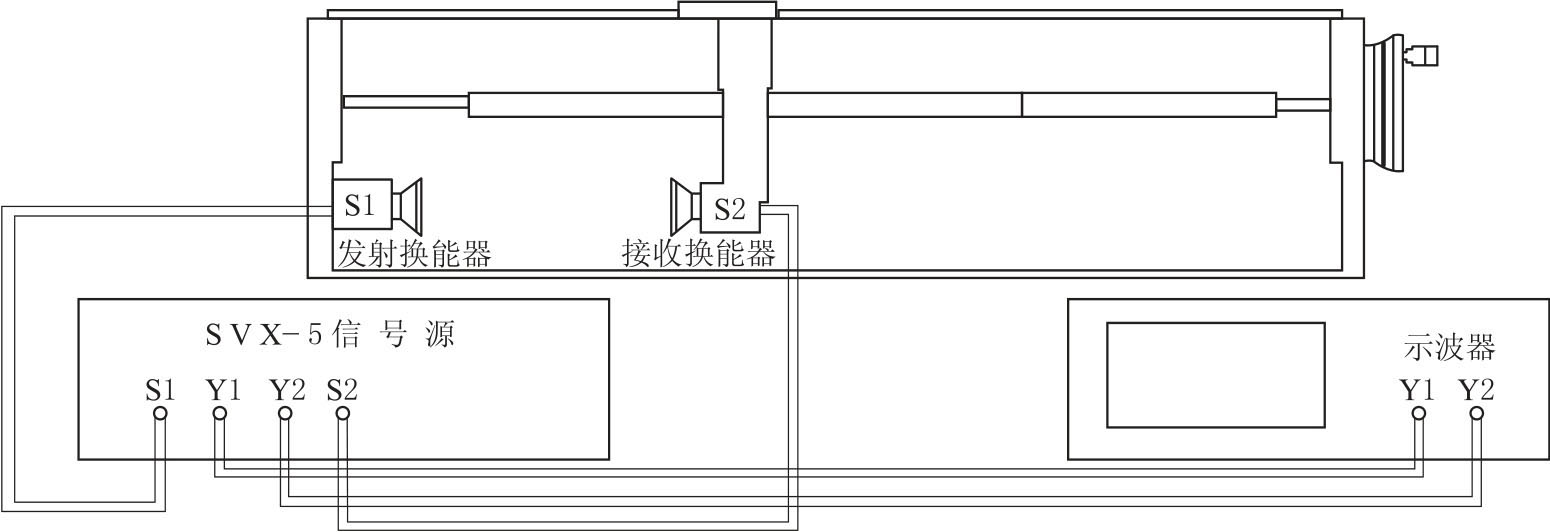
图2-19 共振干涉法（相位比较法）测量声速实验装置
信号源的激励频率等于驻波系统的固有频率（本实验中压电陶瓷的固有频率）时，会产生驻波共振现象，波腹处的振幅达到最大值。
声波是一种纵波。由纵波的性质可以证明，驻波波节处的声压最大。当发生共振时，接收端面处为一波节，接收到的声压最大，转换成的电信号也最强。移动接收器到某个共振位置时，如果示波器上出现了最强的信号，继续移动接收器，再次出现最强的信号时，则两次共振位置之间距离S2的位移为
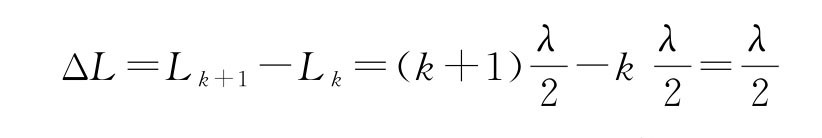
所以当S1和S2之间的距离L 连续改变时，示波器上的信号幅度每一次周期性变化，相当于S1和S2之间的距离改变了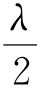
。
（2）相位比较法测量波长λ。波是振动状态的传播，也可以说是位相的传播。如果发射换能器S1和接收换能器S2之间的距离为L，当S1发出的平面超声波通过媒质到达接收器S2，则S2的接收端面与S1的发射端面之间的相位差为
若L=nλ，则Δφ=2nπ，（n=0，1，2，3，…），表明此时S2与S1之间相位差为π的偶数倍，李萨如图形形成斜率为正的一条直线。
若
，则Δφ=（2n+1）π，表明此时S2与S1之间相位差为π的奇数倍，李萨如图形形成斜率为负的一条直线。
若L 为其他值，李萨如图形为椭圆。
所以当S2缓缓远离S1，即S2和S1之间的距离L 连续改变时，相位差从0～π周期性变化，李萨如图形从斜率为正的直线变为椭圆，再变到斜率为负的直线，如图2-20所示。利用李萨如图形形成斜直线来判断位相改变最为敏锐。
图2-20 不同相位差的李萨如图形
重复出现相邻斜率符号相反的直线相位改变Δφ=π，相应S2与S1之间的距离改变
