【实验原理】
1.牛顿环
牛顿环是由一块曲率半径较大的平凸玻璃,以其凸面放在一块光学平板玻璃上构成的。平凸玻璃的凸面和平板玻璃的上表面之间形成了一个空气薄层,如图2-82所示,其厚度由中心到边缘逐渐增加。当平行单色光垂直照射到牛顿环上,经空气薄膜层上、下表面反射的光在凸面处相遇将产生干涉,牛顿环的干涉条纹是以玻璃接触点为中心的明暗相间、内疏外密的同心圆环,如图2-83所示。
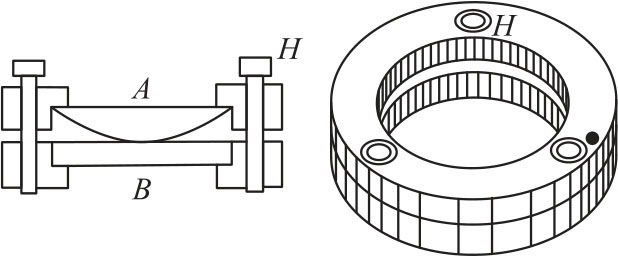
图2-82 牛顿环装置
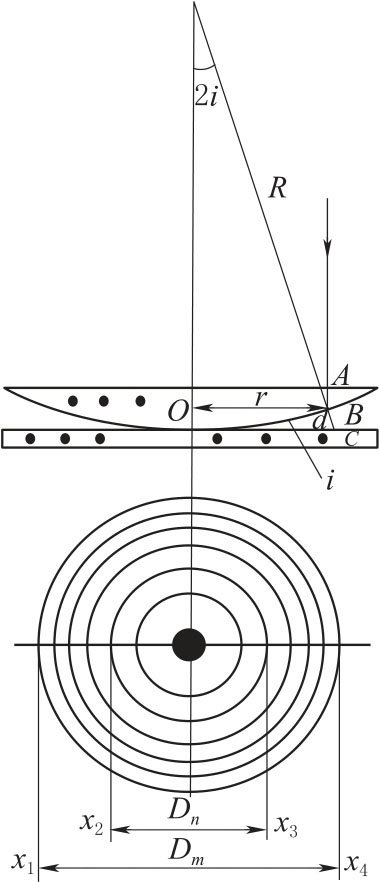
图2-83 钠光垂直照射牛顿环的干涉图样
如图2-83所示,设平凸玻璃面的曲率半径为R,与接触点O 相距为r 处的空气薄层厚度为e,那么由几何关系
因R≫e,所以e2项可以被忽略,有
现在考虑垂直入射到r 处的一束光,它经薄膜层上、下表面反射后在凸面处相遇时其光程差
其中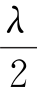 为光从平板玻璃表面反射时的半波损失,把式(2-72)代入得
为光从平板玻璃表面反射时的半波损失,把式(2-72)代入得

由干涉理论,产生暗环的条件为
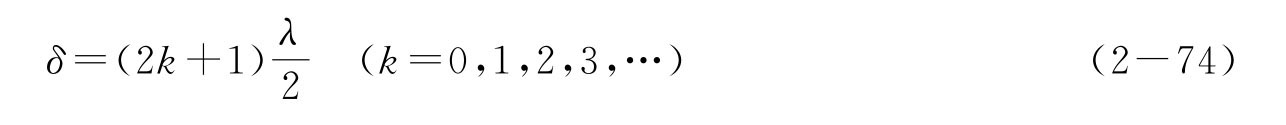
从式(2-73)和式(2-74)可以得出,第k 级暗纹的半径:
所以只要测出rk,如果已知光波波长λ,即可求出曲率半径R,反之,已知R 也可由式(2-75)求出波长λ。在实际测量中由于两块玻璃接触处不是一个理想的点,从而使得干涉图样中心为一暗斑;或者由于空气层中有微小尘粒引起光程的改变,使得干涉图样中心有可能是一个亮斑。以上两种情况将产生暗纹半径测量和干涉级次确定的不准确性。但可以通过测量两个暗环直径平方差的办法加以消除。
由式(2-75),第m 环暗纹和第n 环暗纹的直径可表示为

其中m+x 和n+x 为m 环和n 环的干涉级次,x 为空气层中尘粒引起光程改变而产生的干涉级次的变化量。
把式(2-76)和式(2-77)相减得到
则曲率半径

从式(2-78)可知,只要测出第m 环和第n 环的直径以及数出环数差m-n,就无须确定各环的级数了,且避免了圆心无法准确确定的问题。
2.劈尖
两块平板玻璃,使其一端平行相接,另一端夹入一纸片(或待测样品),这样两块平板玻璃之间形成了一个具有一微小倾角和劈形的空气薄层,这一装置就称为劈尖,如图2-84所示。
当有平行光垂直于下玻璃片照射时,空气薄层上下表面反射光产生干涉,从而形成明暗交替间隔相等的干涉条纹,如图2-85所示。其中第k 级暗纹的光程差满足
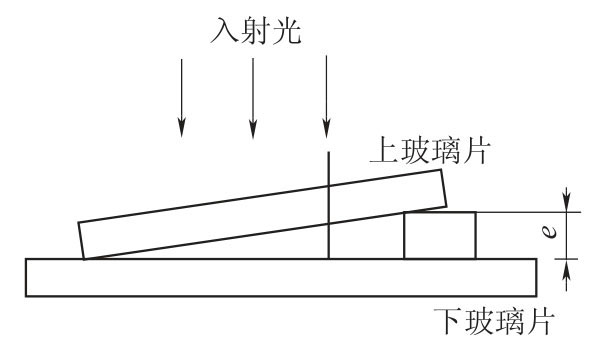
图2-84 劈尖
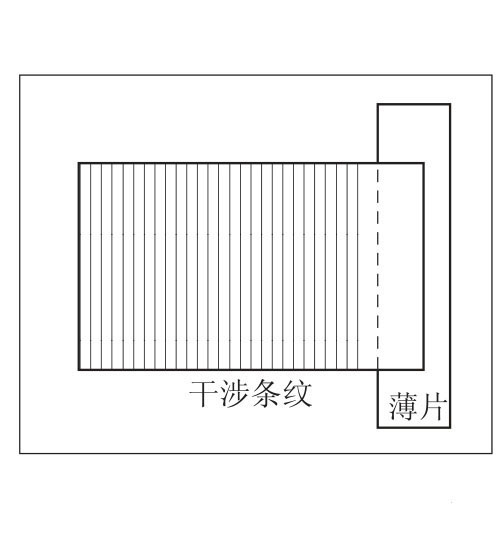
图2-85 劈尖干涉条纹
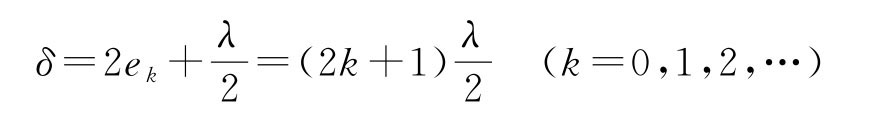
当k=0时,ek=0即为两玻璃接触端。
设纸片处干涉级次为N,由于两暗纹间的厚度差为![]() ,纸片厚度为
,纸片厚度为![]() 。所以只要测出干涉图样中总的条纹数N,即可算出纸片厚度。但实际上N 数值往往很大,不易数出,所以通常我们只要测出10条条纹的间隔L10和玻璃片交线到纸片的距离L,就可算出总的条纹数了
。所以只要测出干涉图样中总的条纹数N,即可算出纸片厚度。但实际上N 数值往往很大,不易数出,所以通常我们只要测出10条条纹的间隔L10和玻璃片交线到纸片的距离L,就可算出总的条纹数了

