【实验原理】
1.“热线法”测量气体导热系数的原理
将待测气体置于沿轴线方向张有一根钨丝的圆柱形容器内(图2-12),并给钨丝提供一定的电流使其温度为T1。设容器内壁的温度近似为室温T2。由于T1>T2,容器中的待测气体必然形成一个沿径向分布的温度梯度。由于待测气体的热传导,将迫使钨丝温度下降,因而无法维持测量室中温度梯度的稳定状态。只有设法维持钨丝的温度恒为T1,容器内待测气体的温度分布才能保持为稳定的径向分布的温度场。
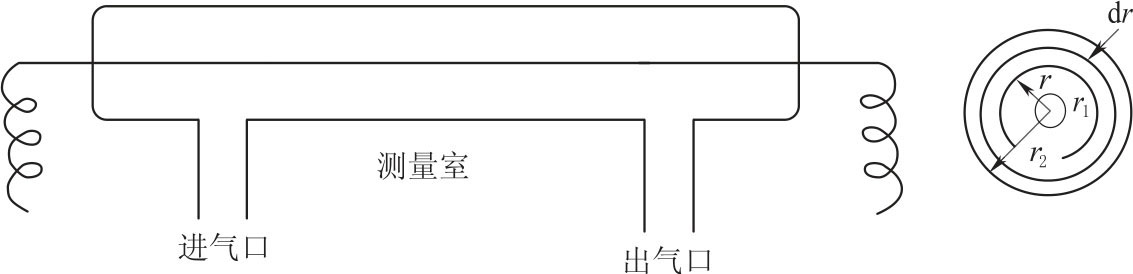
图2-12 圆柱形测量室示意图
本实验就是用热线恒温自动控制系统来维持钨丝温度恒为T1。这样,每秒钟由于气体热传导所耗散的热量就等于维持钨丝的温度恒为T1时所消耗的电功率。不同气体的导热性能(导热系数)不同,则维持钨丝温度恒为T1所消耗的电功率也不同,故可以通过测量钨丝消耗的电功率来求算待测气体的导热系数。
图2-12所示为测量室(盛放待测气体的容器)的示意图。假设钨丝的半径为r1,测量室的内半径为r2,钨丝的温度为T1,长度为l,室温为T2。距热源钨丝r 处取一薄层圆筒状气体层,设其厚度为dr,长为l,内外圆柱面的温差为dT,每秒钟通过该柱面传输的热量为Q,依傅立叶定律有
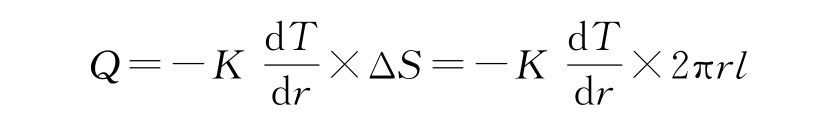
它可改写为
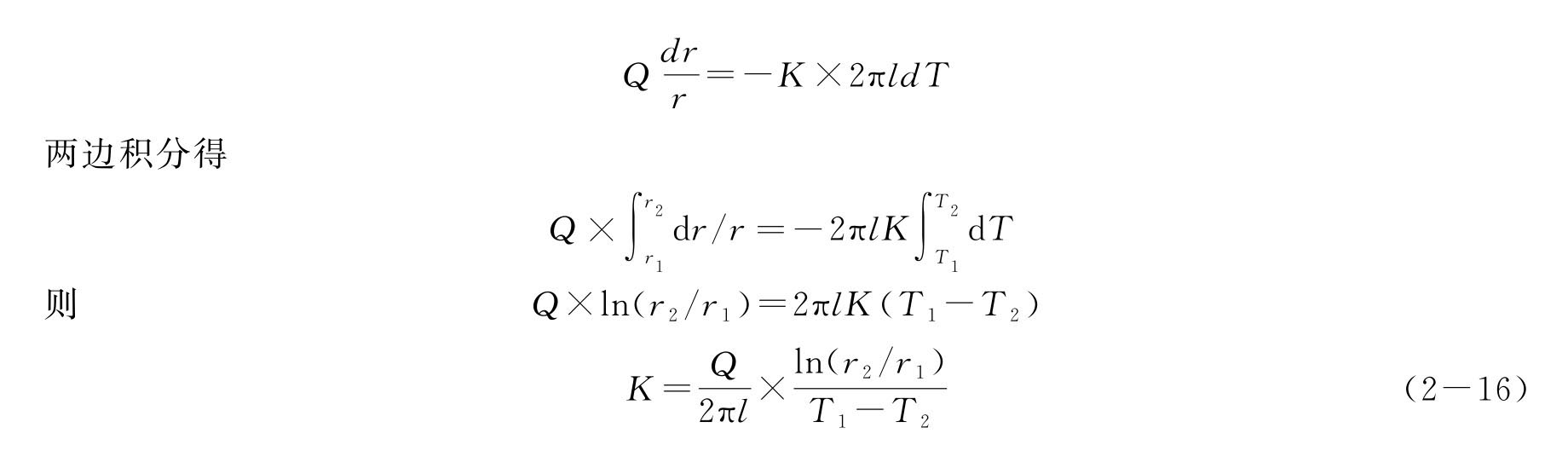
其中K 就是要求的气体导热系数,单位为W/(m·K)。上式中l、r2、r1皆为仪器常数,测量室内壁温度T2可以近似地看作等于室温,问题在于Q 与T1怎么测定?
我们知道,只有不断地为热丝提供电能,才能保持热丝的温度恒为T1,且每秒钟通过气体圆柱面传输的热量Q 事实上就等于钨丝所耗散的电功率,而电功率的测定可通过测量钨丝两端的电压和流经钨丝的电流获得:Q=W=U×I。对于长度为l的钨丝而言,在不同温度时,它的电阻值是不相同的,只要预先标定好钨丝的温度,根据材料电阻率与温度的关系,便可通过测量钨丝的电阻值而求出它的温度T1。
2.二项修正(https://www.daowen.com)
(1)钨丝耗散的总功率,除气体传导的热量之外,尚有钨丝热辐射以及连接钨丝两端的电极棒的传热损失。倘若将测量室抽成真空(低于0.133Pa或10-3Torr),此时为保持钨丝的温度仍为T1所消耗的电功率,将主要用于钨丝的热辐射与电极棒的传热损失,它等于:
故气体每秒钟所传导的热量Q低(指低气压条件下气体每秒钟传导的热量)应为
在实际测量过程中,由于测量室的外管壁温度会有所提高,带来的系统误差使Q低值偏小。为了消除这一系统误差,经长期实验发现,在以上公式中用乘1.2的系数加以修正即可
(2)为了减少气体对流传热的影响,测量应在低气压(133.3~1333Pa或1~10Torr)条件下进行。因为在低气压的情况下,通过Q低算出的K低(低气压下的气体导热系数)和测量时测量室内的压强P 存在着下述关系:

从式(2-16)可见Q 与K 成正比(因为r2、r1、l 为仪器常数,T1、T2在测量中为恒定值),因此式(2-18)中的K低和K 可以用Q低和Q 来代替,只是系数A 要转换为另一系数B,于是可将式(2-18)改写为以下的形式:

本实验是在不同压强P 的情况下,测出相应的Q低,然后以1/P 为横坐标,1/Q低为纵坐标作图,所得到的实验曲线将近似为一直线。此直线在纵坐标上的截距即为1/Q,这就是所谓用外推法求Q 值,将所得的Q 代入式(2-16),便得到欲求的气体在T1~T2时的平均导热系数。
综上所述,测量气体导热系数的过程,实际上就是测量不同低气压(P)情况下相应的Q低,这里[Q低=(UPIP-U空I空)×1.2],通过1/P 与1/Q低作图求出截距1/Q,将Q 及已知的l、r1、r2、T1、T2代入式(2-16)而求出气体在T1~T2之间的平均导热系数K。
本实验装置如图2-13所示,其中各部分的作用分别如下。
热线恒温调节电位器:它可以设定钨丝(热线)初始温度的高低,并通过仪器自动恒温控制系统保证热线在不同气压条件下皆保持同一温度设定值T1。
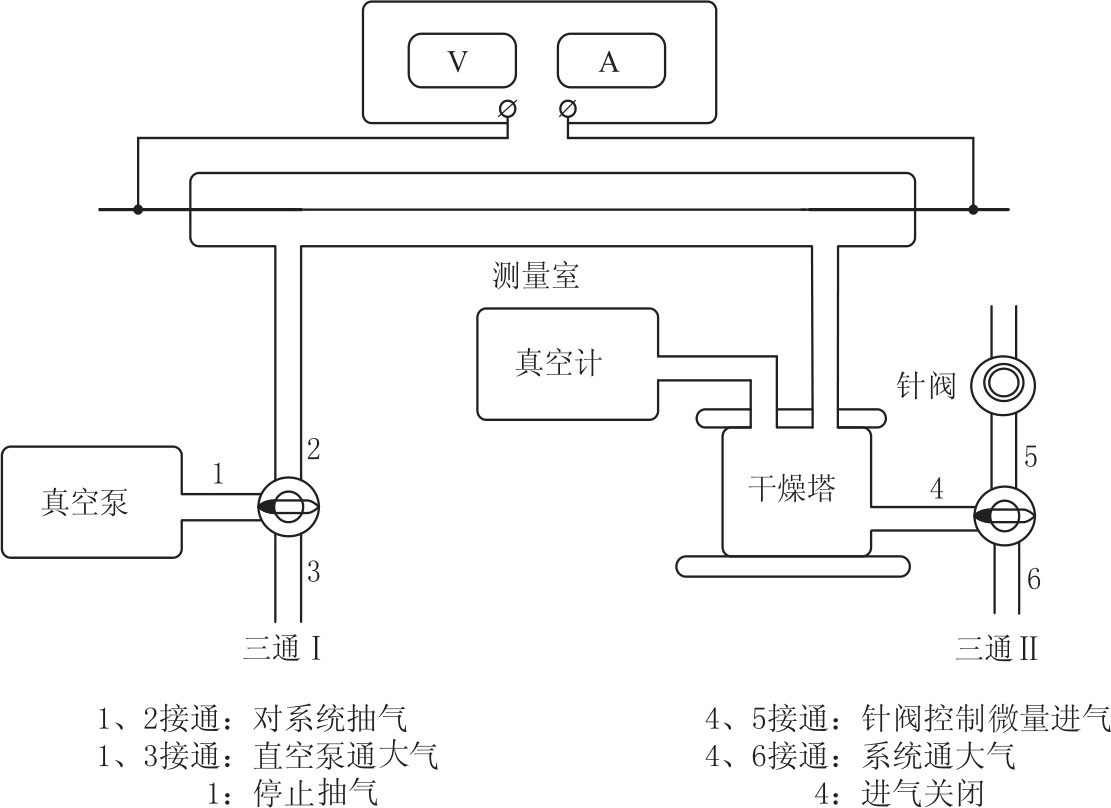
图2-13 实验装置
测量室: 作为待测气体的存储与测量空间;真空计:用于测量系统的真空度;干燥塔:用于对待测气体干燥除湿,同时缓冲系统气压变化速率,从而保护电子真空计的压力传感器;针阀:用于调节待测气体的进气速率(注意:该阀仅用于流量的调节,而不可作为截止阀使用);三通Ⅰ:用来转换1、2接通(真空泵对系统抽气状态)或1、3接通(真空泵进气口通大气状态,以免真空泵回油);三通Ⅱ:可转换4、5接通(针阀控制进气状态)或4、6接通(系统直接通大气状态)。
若三通Ⅰ为1、2接通,三通Ⅱ为关闭状态,则此时对测量室及全系统抽气。
