【实验原理】
2026年01月14日
【实验原理】








1.扭摆的简谐运动
扭摆的结构如图2-6所示,其垂直轴1上装有一根簿片状的螺旋弹簧2,用以产生恢复力矩。在轴上方可以装上各种待测物体。垂直轴与支座间装有轴承,使摩擦力矩尽可能降低。为了使垂直轴1与水平面垂直,可通过底脚螺丝钉3来调节,4为水平仪,用来指示系统调整水平。
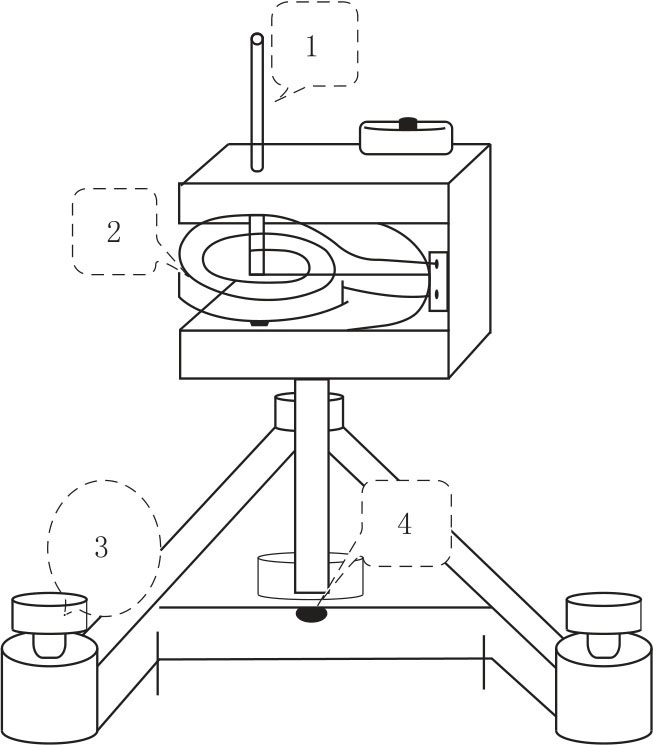
图2-6 扭摆结构图
将物体在水平面内转过一角度θ 后,在弹簧的恢复力矩作用下,物体就开始绕垂直轴作往返扭转运动。根据胡克定律,弹簧受扭转而产生的恢复力矩M 与所转过的角度成正比,即
式中:K 为弹簧的扭转常数。
根据转动定律
式中:I 为转动惯量;β 为角加速度。(https://www.daowen.com)
由式(2-5)与式(2-6)得
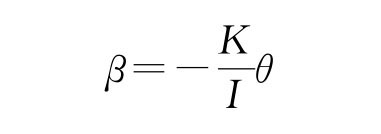
其中![]() ,忽略轴承的摩擦力矩,则有
,忽略轴承的摩擦力矩,则有
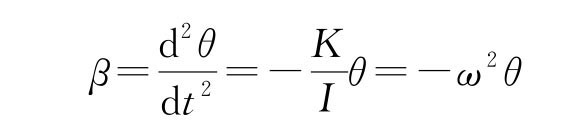
此方程表明忽略轴承摩擦力矩的扭摆运动是角简谐振动,且角加速度β 与角位移θ 成正比,方向相反。此方程的解为
式中:A 为简谐振动的角振幅;φ 为初位相;ω 为角频率。
此简谐振动的周期为

利用式(2-7),测得扭摆的周期T,在I 和K 中任何一个量已知时即可计算出另一个量。
本实验用一个转动惯量已知的物体(几何形状有规则,根据它的质量和几何尺寸用理论公式计算得到),测出该物体摆动的周期,再算出本仪器弹簧的K 值。若要测量其他形状物体的转动惯量,只需将待测物体安放在本仪器顶部的各种夹具上,测定其摆动周期,由式(2-7)即可计算出该物体绕转动轴的转动惯量。转动惯量单位为kg·m2。
2.平行轴定理
若质量为m 的物体绕通过质心轴的转动惯量为Ic,当转轴平行移动距离x 时(图2-7),则此物体对新轴的转动惯量I0=Ic+mx2,称为转动惯量的平行轴定理。
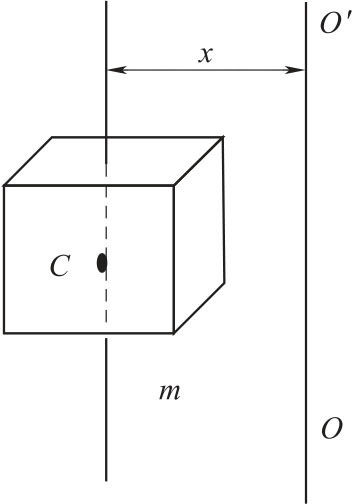
图2-7 平行轴定理
