【数据与结果】

【数据与结果】

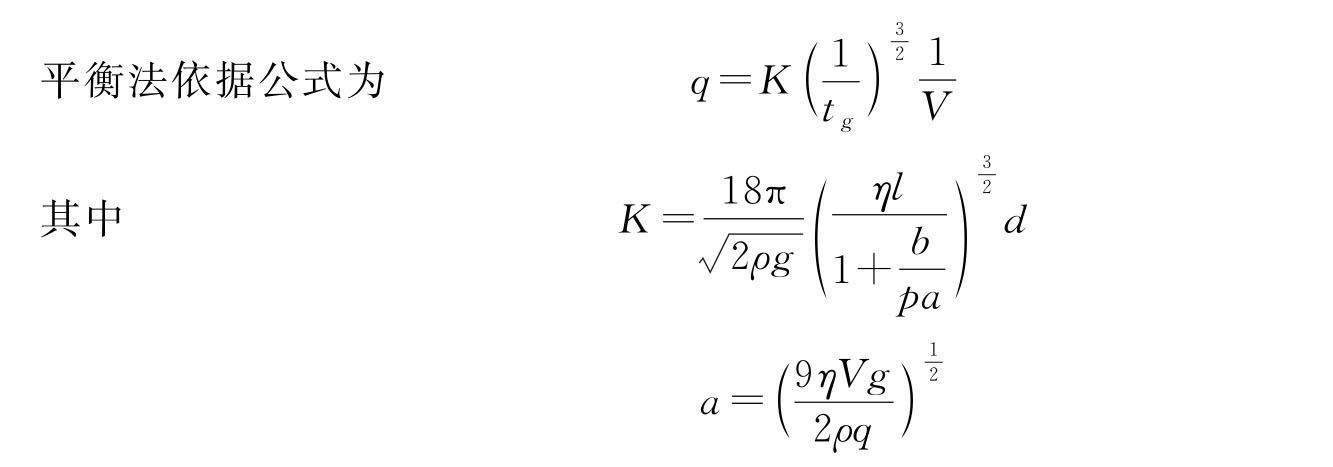
油的密度　　ρ=981kg·m-3

重力加速度　g=9.80m·s-2

空气黏滞系数　　η=1.83×10-5kg·m-1·s-1

油滴匀速下降距离　l=2.00×10-3m

修正常数　b=6.17×10-6m·cmHg

大气压强　p=76.0cmHg

平板极板间的距离　d=5.00×10-3m

式中的时间tg应为测量数次时间的平均值。实际大气压由气压表读出。

将上述数据代入式（3-16）得油滴的电荷量

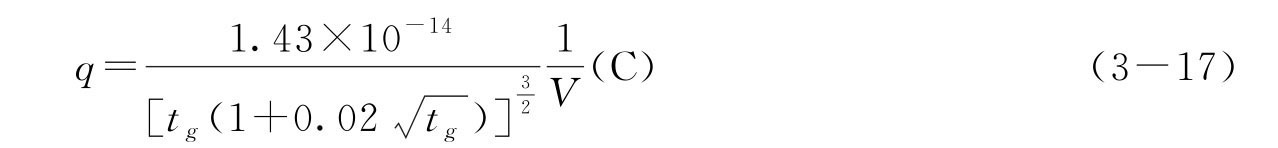
计算出各油滴的电荷后，求它们的最大公约数，即为基本电荷e 值。若求最大公约数有困难，可用作图法求e 值，设实验得到m 个油滴的带电量分别为q1，q2，…，qm，由于电荷的量子化特性，应有qi=nie，此为一直线方程，n 为自变量，q 为因变量，e 为斜率。因此n 个油滴对应的数据在n～q 坐标中将在同一条直线上，若找到满足这一关系的直线，就可用斜率求得e 值。

将e 的实验值与公认值比较，求百分误差。

注：用式（3-17）计算q 虽然是近似的，却极其方便。原因是油的密度、空气的黏滞系数都是温度的函数，重力加速度和大气压强随实验地点和条件而变化。用式（3-16）可准确计算油滴电荷量，但要查当时温度下油的密度、空气的黏滞系数及大气压强。