实验数据处理方法
物理实验中常用的数据处理方法有列表法、作图法、逐差法、最小二乘法线性拟合等。
1.列表法
在记录和处理数据时，要将数据列成表格，用表格表示数据显得清楚明了，有关物理量之间的关系以及数据和处理数据过程中存在的问题都能在表格中显示出来。列表的基本要求如下：
（1）各栏目均应标注名称和单位。
（2）列入表中的主要应是原始数据，计算过程中的一些中间结果和最后结果也可列入表中，但应写出计算公式，从表格中要尽量使人看到数据处理的方法和思路，而不能把列表变成简单的数据堆积。
（3）栏目的顺序应充分注意数据的联系和计算的程序，力求条理化和简明化。
（4）必要的附加说明，如测量仪器的规格、测量条件、表格名称等。
2.作图法
用图线表示实验结果可以形象、直观、简便地表达物理量间的变化关系。其作用如下：①研究物理量之间的变化规律，找出对应的函数关系或经验公式；②求出实验的某些结果，如直线方程y=kx+b，可根据曲线斜率求出k 值，从曲线截距获取b 值；③用内插法可从曲线上读取没有进行测量的某些量值；④用外推法可从曲线延伸部分估读出原测量数据范围以外的量值；⑤作图连线对数据点可起到平均的作用，从而减少随机误差。
要特别注意的是，实验作图不是示意图，而是用图来表达实验中得到物理量间的关系，同时还要求反映出测量的准确程度，因而必须按一定原则作图。
（1）作图规则。
1）选用合适的坐标纸：根据作图参量的性质，选用毫米直角坐标纸、双对数坐标纸、单对数坐标纸或其他坐标纸等。坐标纸的大小应根据测得数据的大小、有效数字多少及结果的需要来定。
2）坐标轴的比例与标度：①一般以横轴代表自变量，纵轴代表因变量；②轴的末端近旁标明所代表的物理量及其单位；③适当选取横轴和纵轴的比例和坐标起点，使曲线大体上充满整个图纸；④图上实验点的坐标读数的有效数字位数不能少于实验数据的有效数字位数；⑤横轴和纵轴的标度可以不同，交点可不为零。
3）曲线的标点与连线：数据点应该用大小适当的明显标志×、+、△，同一张图上的几条曲线应采用不同的标志；连线要光滑，不一定要通过所有的数据点。因为每个实验点的误差情况不一定相同，因此不应强求曲线通过每个实验点而连成折线（仪表的校正曲线不在此例）。应该按实验点的总趋势连成光滑的曲线或直线，要做到图线两侧的实验点与图线的距离最为接近且分布大体均匀。
4）写明图线特征和名称：利用图上空白位置注明实验条件和从图线上得出某些参数，如截距、斜率、极大值、极小值、拐点和渐近线等。有时需要通过计算求一些特征量，图上还须标出被选计算点的坐标及计算结果，最后写上图的名称。有时也可列出主要的实验对象和条件等。
（2）图解法求拟合直线的斜率和截距。设拟合直线为y=a+bx。
1）求斜率：
。可在所作直线上选取两点P1（x1，y1）和P2（x2，y2）代入上式求得。P1与P2两点一般不取原来测量的数据点，并且要尽可能相距得远些，在图上标出它们的坐标。为便于计算，x1、x2两数值可选取整数，斜率的有效数字要按有效数字规则计算。
2）求截距：如果横坐标的起点为零，则直线的截距可直接从图线中读出，否则可用下式计算截距：
。
例1-5 用惠斯登电桥测定铜丝在不同温度下的电阻值，数据见表1-1。试求铜丝的电阻与温度的关系。
表1-1 铜丝电阻与温度的关系
解：以温度t为横坐标，电阻Rt为纵坐标。横坐标选取2mm 代表10℃，纵坐标1mm代表0.20Ω。绘制铜丝电阻与温度曲线如图1-2所示。由图中数据点分布可知，铜丝电阻与温度为线性关系，满足下面线性方程
在图线上取两点（图1-2），计算斜率b 和截距a 得
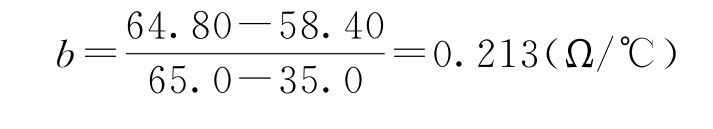
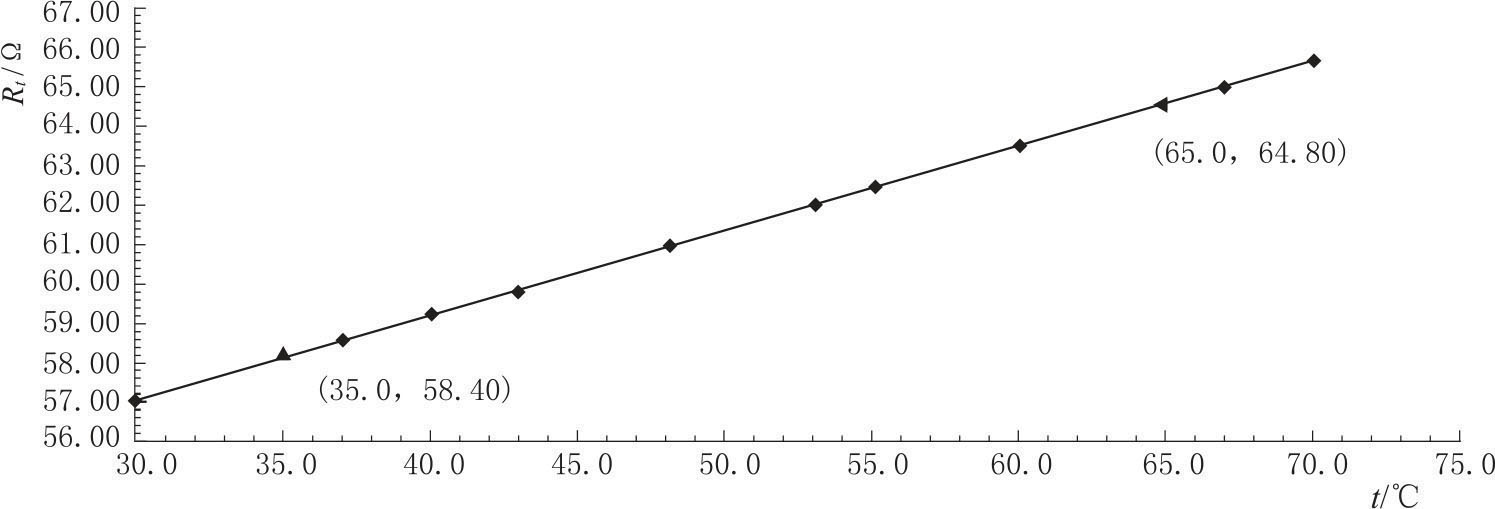
图1-2 铜电阻Rt-t关系图
所以，铜丝电阻与温度的关系为
如果两物理量成正比，在实验中常作多次测量，用图解法求比例系数，这样做可使结果比单次测量准确得多。
3.逐差法
当两个被测物理变量之间存在多项式函数关系，且自变量为等间距变化时，常常用逐差法处理测量数据，既能充分利用实验数据，又具有减小误差的效果。
逐差法就是把实验得到的偶数组数据分成前后两组，将对应项分别相减。另外，还可以对实验数据进行逐次相减，这样可验证被测量之间的函数关系，及时发现数据差错或数据规律。本书中有杨氏模量实验、声速测量实验、牛顿环实验、迈克尔逊干涉测激光波长实验、夫兰克-赫兹实验等都要用逐差法处理数据。
下面举例说明用逐差法处理实验数据过程和方法。
例1-6 每个砝码质量为100克，实验测得弹簧所挂砝码与弹簧长度（单位：cm）关系数据见表1-2。求弹簧劲度系数。
表1-2 弹簧劲度系数数据记录表
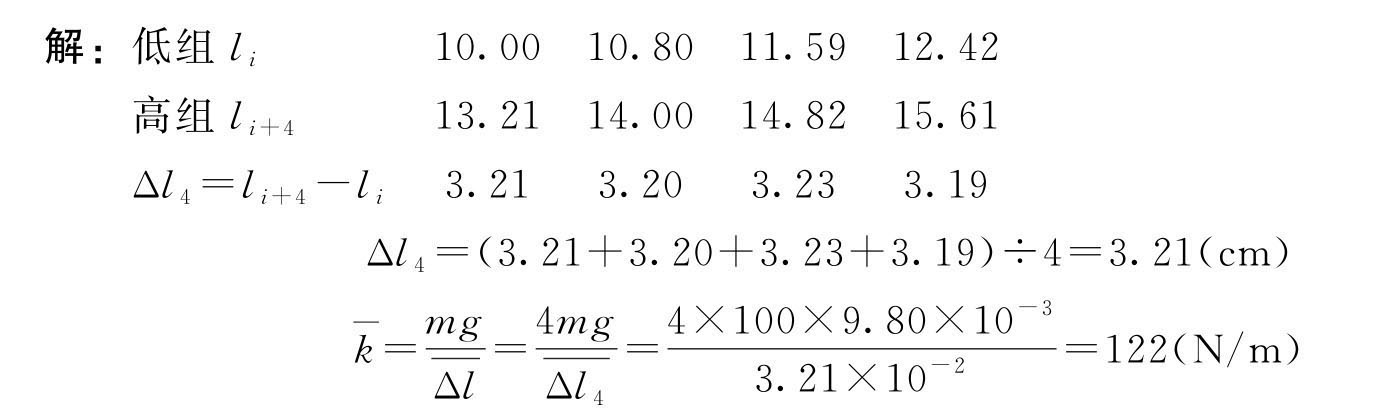
也可以用逐差法直接列式计算，测量次数n=8，即n/2=4。
Δl1=13.21-10.00=3.21；Δl2=14.00-10.80=3.20；Δl3=14.82-11.59=3.23；Δl4=15.61-12.42=3.19。
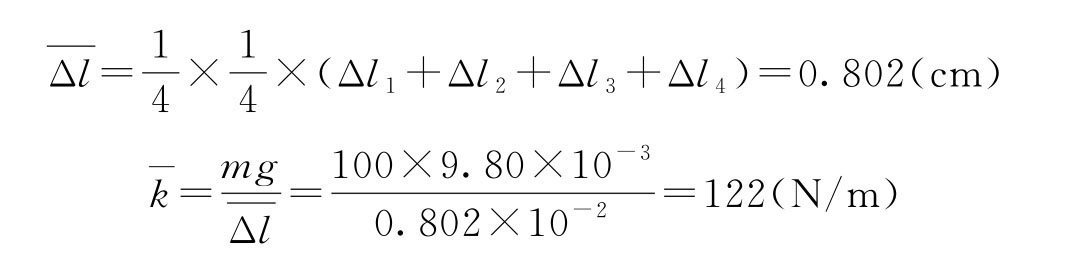
4.实验数据的线性拟合（线性回归）
作图法虽然在数据处理中是一个很便利的方法，但它不是建立在严格统计理论基础上的数据处理方法，在作图纸上人工拟合直线（或曲线）时有一定的主观随意性，往往会引入附加误差，尤其在根据图线确定常数时，这种误差有时很明显。为了克服这一缺点，在数据统计中研究了直线拟合问题（或称一元线性回归问题），常用的是一种以最小二乘法为基础的实验数据处理方法。感兴趣同学可自行查阅相关资料，大学物理实验中为简化，略去。
此外相关计算机软件如Excel，以及专业的Matlab、Oringe、Mathematics等可以提供各种所需的数据处理功能，有余力同学可学习参考。