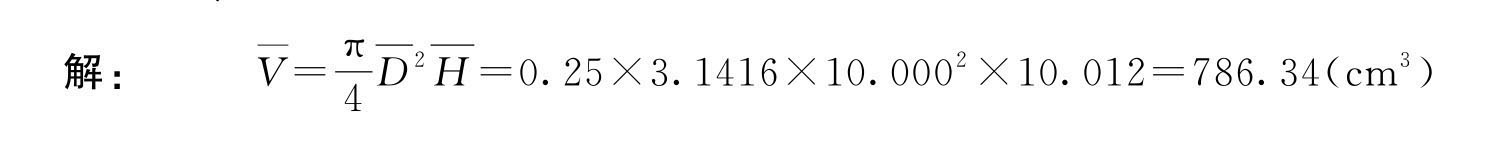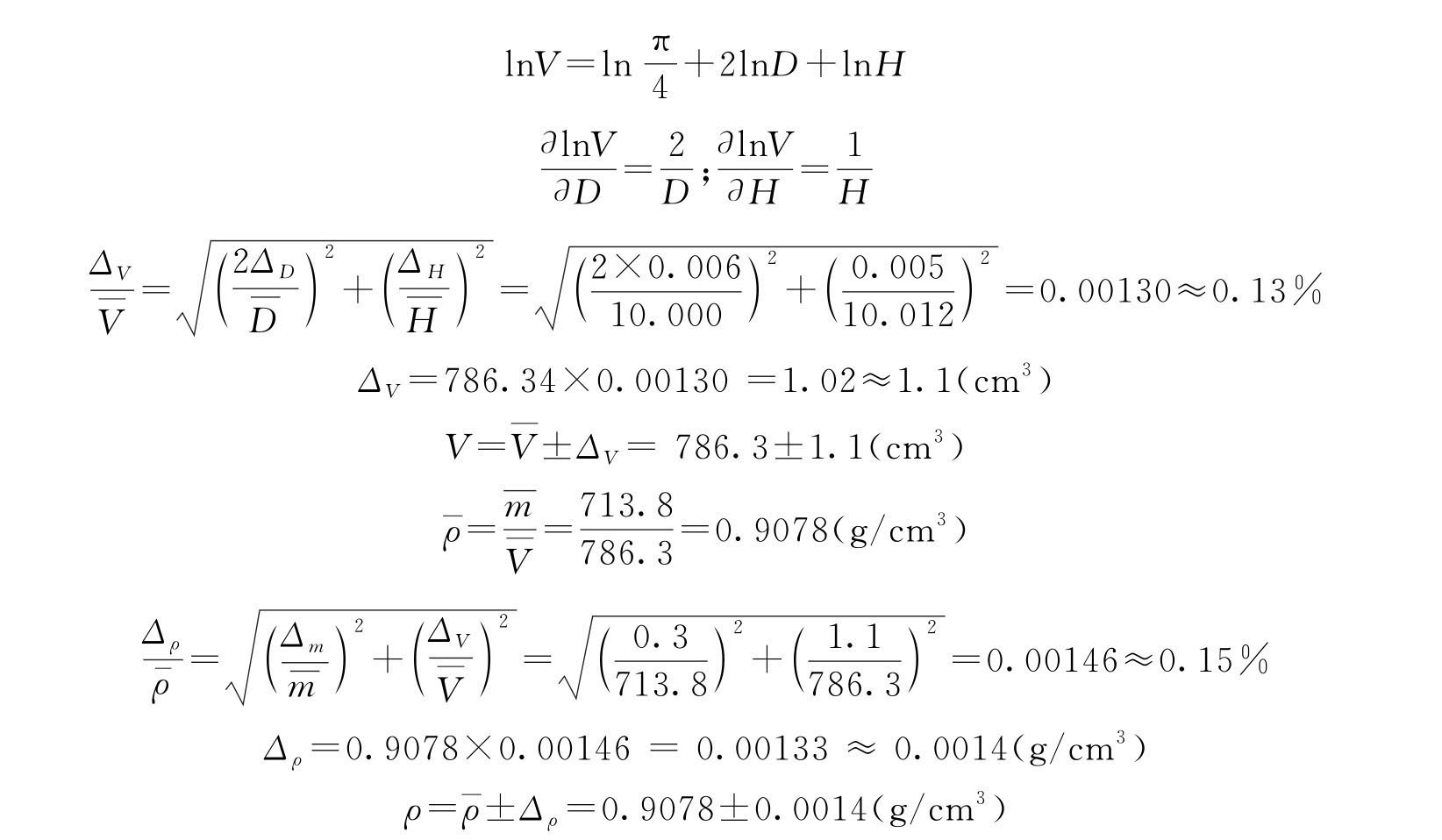不确定度及估算方法
1.不确定度概念
一个完整测量不仅给出测量量大小，同时也要给出不确定度。用不确定度来表征该测量结果可信赖程度。
由于真值不知道，因而无法确定误差的大小。因此，实验数据的处理只能求出实验的最佳估计值及其不确定度，通常把测量结果表示为
测量值=最佳估计值±不确定度（单位）
如基本物理常数基本电荷表达式：
基本电荷 e=（1.6021773±0.0000003）×10-19C
何为不确定度？不确定度是指由于测量误差的存在而对被测量值不能肯定的程度，或者说它表征被测量的真值在某个量值范围的一个客观的评定，是测量结果携带的必要参数。由此可见，不确定度与误差有区别。误差是一个理想的概念，一般不能精确知道，但不确定度反映误差存在分布的范围，可由误差理论求得。
不确定度一般包含多个分量，按其数值的评定方法可归并为两类：
（1）A 类不确定度：多次重复测量时用统计方法计算的那些分量ΔA。
（2）B类不确定度：用其他非统计方法估出的那些分量ΔB，它们只能基于经验或其他信息作出评定。
2.直接测量不确定度估算方法
（1）A 类不确定度分量的估算。实际测量中，一般只能进行有限次测量，这时随机误差不完全服从正态分布规律，而是服从t分布的规律。这种情况下，不确定度A 类分量ΔA等于测量值的标准偏差Sx乘以一因子
，但在大学物理实验中为简化起见，直接取
（2）B类不确定度分量的估算。一般用近似的等价标准差ΔB表征：ΔB=Δ仪/C。
其中，Δ仪为仪器误差，C 为修正因子。但在大学物理实验中为简化起见，直接取C=1，则ΔB=Δ仪，Δ仪可由以下途径获得：
1）仪器铭牌或说明书给出。
2）仪表准确度等级获得。Δ仪=k%×量程，式中k 为仪器准确度等级。
3）连续读数仪器Δ仪=最小分度值一半。
4）非连续读数仪器Δ仪=最小分度值。
5）数字式仪表取末位±1或±2。
例如0～25mm 的一级千分尺（螺旋测微器）的仪器误差Δ仪=0.004mm（计量标准规定）；0～300mm 的游标卡尺的仪器误差Δ仪=0.02mm（游标有50分格）；普通米尺Δ仪=0.5mm；如果数字万用表的读数为15.25V，则Δ仪=0.01V。
实验室常用测量仪器中连续读数仪器指米尺、千分尺、各类指针式仪表（电压、电流、欧姆表等）、温度计等；非连续读数仪器指游标卡尺、分光计、电阻箱、箱式电桥等。在工业或商业用途上，仪器误差置信概率为95%。
（3）合成不确定度。A 类和B 类分量采用“方、和、根”，得到直接测量的合成不确定度
不确定度大小与置信概率有关。国家计量技术规范《测量不确定度评定与表示》（JJF 1059—1999）推荐三种置信概率，分别是68%、95%和99%，给出测量结果不确定度时，除P=95%外，其他两个必须注明P 值。
例1-1 用千分尺（Δ仪=0.004mm）对一钢丝直径d 进行六次测量，读数分别为1.577mm、1.580mm、1.578mm、1.581mm、1.575mm、1.576mm，千分尺零位读数（零误差）为0.006mm，求出测量结果。
解：读数平均值
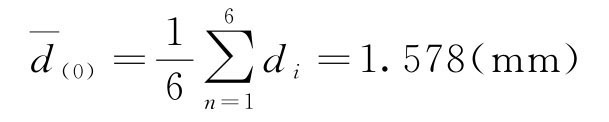
测量平均值
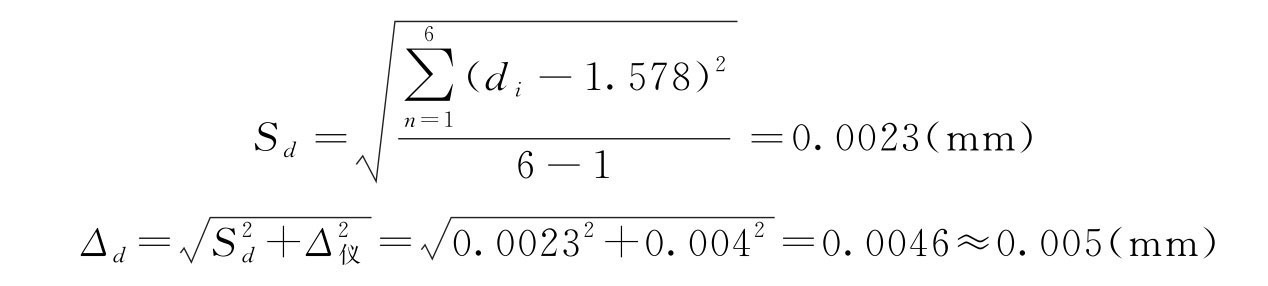
钢丝直径测量结果 d=1.572±0.005（mm）
请特别注意：以后在大学物理实验报告中，任何一个物理量的测量结果都应该以上述结果表达形式给出，即必须表示成： 测量值=最佳估计值±不确定度（单位）。
3.间接测量不确定度估算
上面介绍的是直接测量，对于间接测量的物理量处理如下。设间接测量值y 是各相互独立的直接测量值x1，x2，…，xm的函数
其中
，
，…，
［按照上面介绍的方法，每个直接测量结果表示成测量值=最佳估计值±不确定度（单位）］。
把每个直接测量的平均值带入，则间接测量值y 最佳估算值
对函数求偏微分
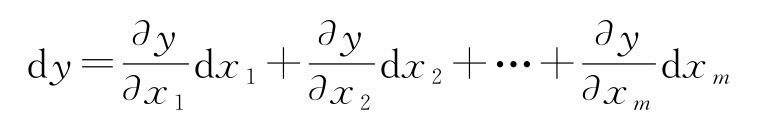
因不确定度Δ 是微小的量，相当于数学中“增量”，因此间接测量的计算公式与数学中全微分公式基本相同。不同之处：①要用不确定度Δx等替代微分dx 等；②要考虑不确定度合成的统计性质，一般是用“方、和、根”的方式进行合成。于是间接测量不确定度
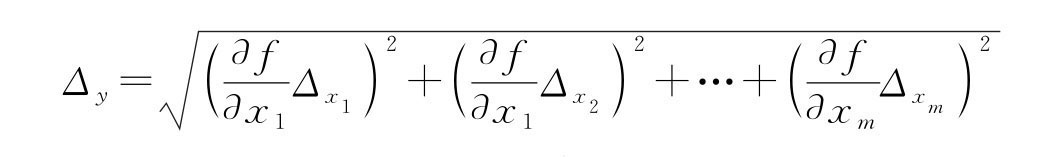
和直接测量一样，间接测量结果也应该表示为
对于积商形式函数，两边取对数
间接测量值y 的相对不确定度
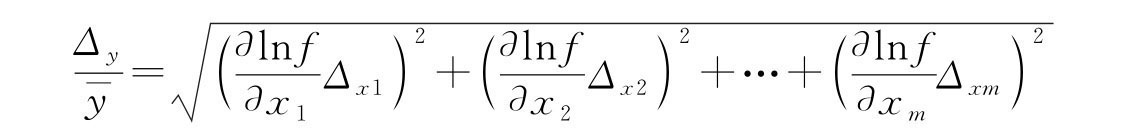
上述求解间接测量值y 的不确定度过程仅供参考，大学物理实验中，对于间接测量的物理量，一般都已给出求解测量值y 的不确定度的具体公式，无须再去推导。
例1-2 设A，B，C 是独立变量，求下列两种情形下y 不确定度：
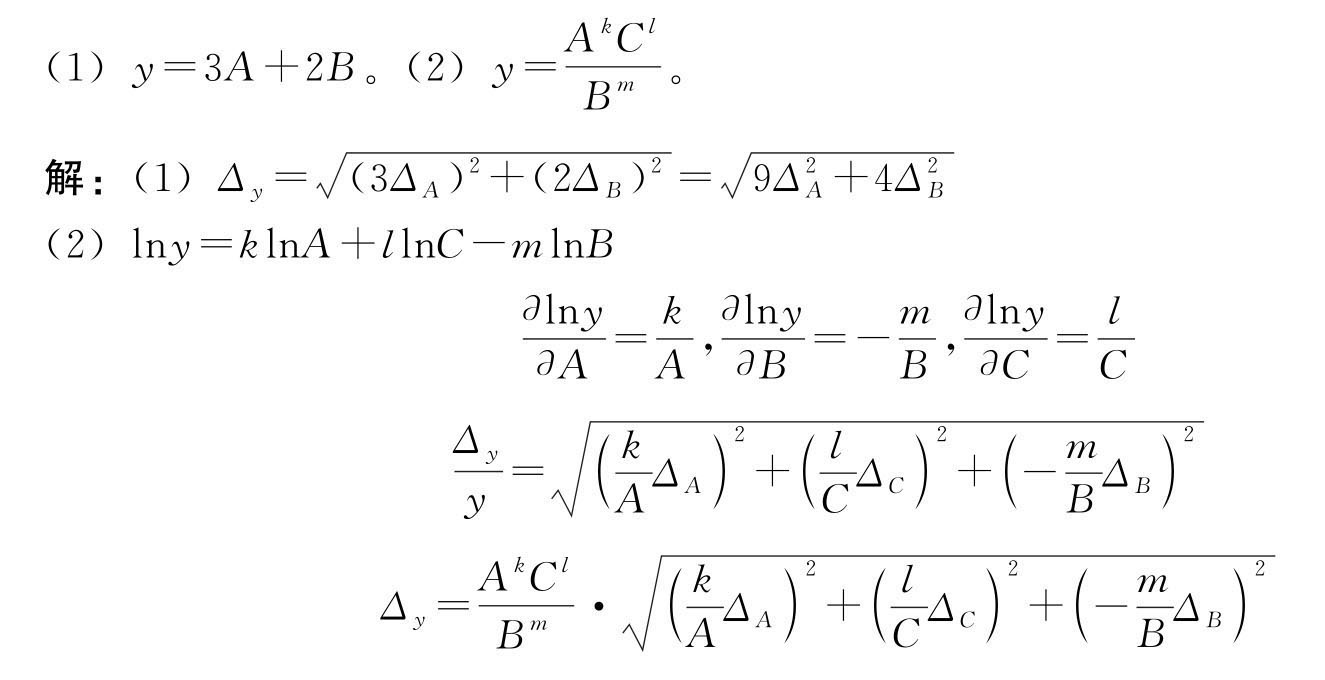
例1-3 圆柱体的直径和高分别为D=10.000±0.006（cm），H=10.012±0.005（cm），质量m=713.8±0.3（g），圆柱体体积公式为
，取π=3.1416，试计算圆柱体体积V 和密度ρ。
