【实验原理】
2026年01月14日
【实验原理】










当半径为r 的光滑圆球,以速度v 在均匀的无限宽广的液体中运动时,若速度不大,球也很小,在液体中不产生涡流的情况下,斯托克斯指出,球在液体中所受到的阻力F 为
式中:η 为液体的黏滞系数,单位是Pa·s。
此式称为斯托克斯公式。从式(2-9)可知,阻力F 的大小和物体运动速度成正比。
当质量为m、体积为V 的小球在密度为ρ 的液体中下落时,作用在小球上的力有三个,即:①重力mg;②液体的浮力ρVg;③液体的黏性阻力6πηvr。这三个力都作用在同一铅直线上,重力向下,浮力和阻力向上,如图2-10所示。球刚开始下落时,速度v 很小,阻力不大,小球作加速度下降。随着速度的增加,阻力逐渐加大,速度达一定值时,阻力和浮力之和将等于重力,那时物体运动的加速度等于零,小球开始匀速下落,即
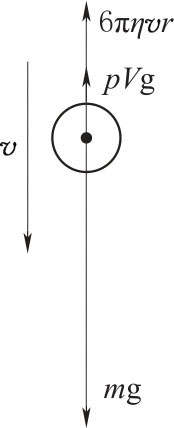
图2-10 小球匀速下落受力示意图
此时的速度称为终极速度,由此式可得(https://www.daowen.com)
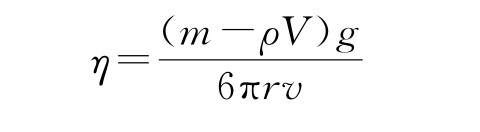
将![]() 代入上式,得
代入上式,得

由于液体在容器中,而不满足无限宽广的条件,这时实际测得的速度v0和上述式中的理想条件下的速度v 之间存在如下关系
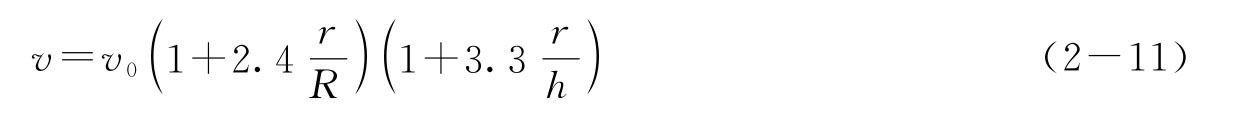
式中:R 为盛液体圆筒的内半径;h 为筒中液体的深度。
将式(2-11)代入式(2-10),得出
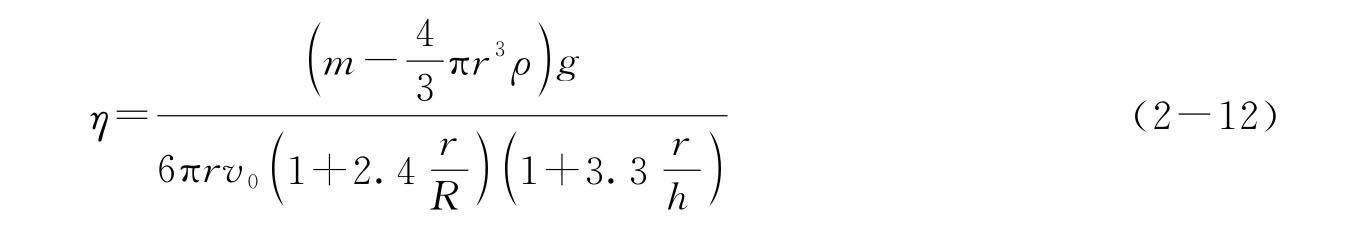
其次,斯托克斯公式是假设在无涡流的理想状态下导出的。实际小球下落时不会是这样理想状态,因此还要进行修正。已知在这时的雷诺数Re 为

当雷诺数不甚大(一般在Re<10)时,斯托克斯公式修正为
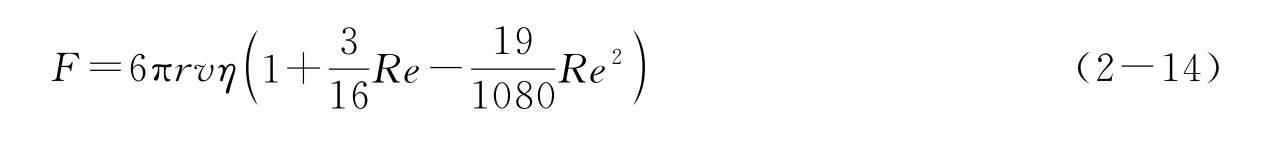
则考虑此项修正后的黏滞系数,测得值η0等于
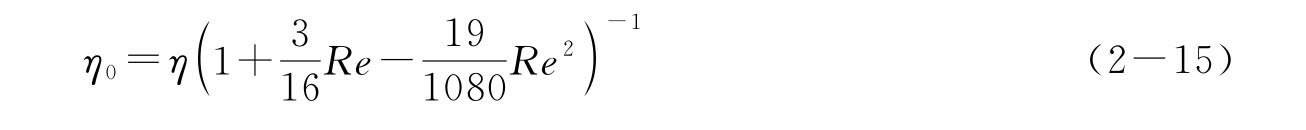
实验时,先由式(2-12)求出近似值η,用此η 代入式(2-13)求出Re,最后由式(2-15)求出最佳值η0。黏滞系数单位为Ns/m2。
