【实验原理】
R、L、C 组件的不同组合，可以构成RC、RL、LC 和RLC 电路，这些不同的电路对阶跃电压的响应是不同的，从而有一个从一种平衡态转变到另一种平衡态的过程，这个转变过程即为暂态过程。
1.RC 电路
在由电阻R 及电容C 组成的直流串联电路中，暂态过程即是电容器的充放电过程，如图3-33所示，当开关K 打向位置1时，电源对电容器C 充电，直到其两端电压等于电源电压E，在充电过程中回路方程为
考虑到初始条件t=0时，uC=0，得到方程的解：
此解表示电容器两端的充电电压是按指数增长的一条曲线，稳态时电容两端的电压等于电源电压E，如图3-34（a）所示。式中RC=τ 具有时间量纲，称为电路的时间常数，是表征暂态过程进行得快慢的一个重要的物理量，由电压uc上升到0.63E 所对应的时间即为τ。
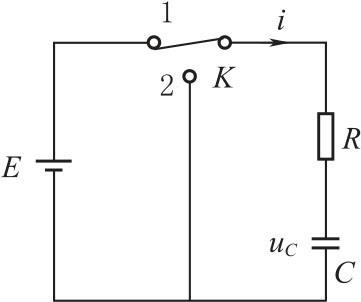
图3-33 RC 电路
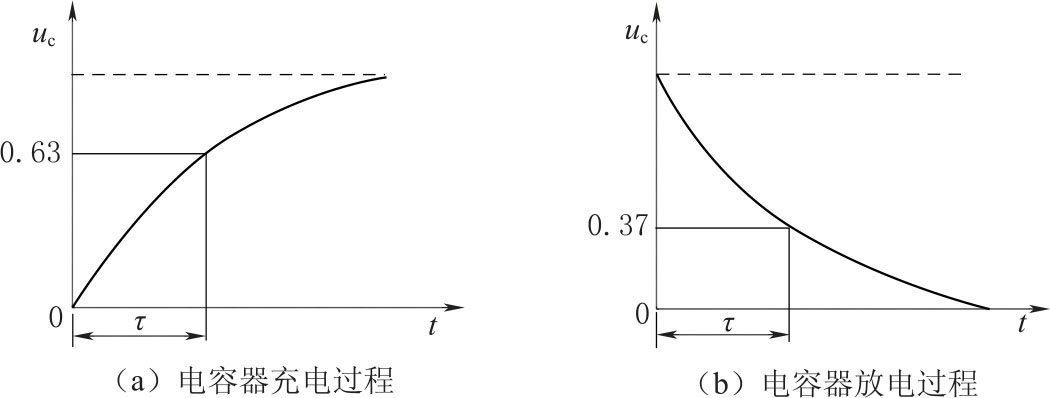
图3-34 RC 电路的充放电曲线
当把开关K 打向位置2时，电容C 通过电阻R 放电，回路方程为
结合初始条件t=0时，uC=E，得到方程的解：
此解表示电容器两端的放电电压按指数规律衰减到0，τ 也可由此曲线从E 衰减到0.37E 所对应的时间来确定。充放电曲线如图3-34所示。
2.RL 电路
RL 电路由电阻R 及电感L 串联组成，如图3-35所示。
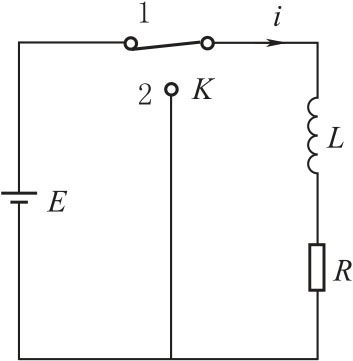
图3-35 RL 电路
当开关K 置于1时，由于电感L 的自感作用，回路中的电流不能瞬间突变，而是逐渐增加到最大值E/R。回路方程为
考虑到初始条件t=0时，i=0，可得方程的解：
可见，回路电流i是经过一指数增长过程，逐渐达到稳定值E/R 的。i 增长的快慢由时间常数τ=L/R 决定，如图3-36（a）所示。
当开关K 打到位置2时，电路方程为
由初始条件t=0，i=E/R，可以得到方程的解：
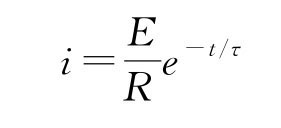
此解表示回路电流i从E/R 按指数逐渐衰减到0，如图3-36（b）所示。
3.RLC 电路
以上讨论的都是理想化的情况，即认为电容和电感中都没有电阻，可实际上不但电容和电感本身都有电阻，而且回路中也存在回路电阻，这些电阻是会对电路产生影响的，电阻是耗散性组件，将使电能单向转化为热能。可以想象，电阻的主要作用就是把阻尼项引入到方程的解中。
充电过程：在一个由电阻R、电容C 及电感L 组成的直流串联电路中（图3-37），当把开关K 置于1时，电源对电容器进行充电，回路方程为
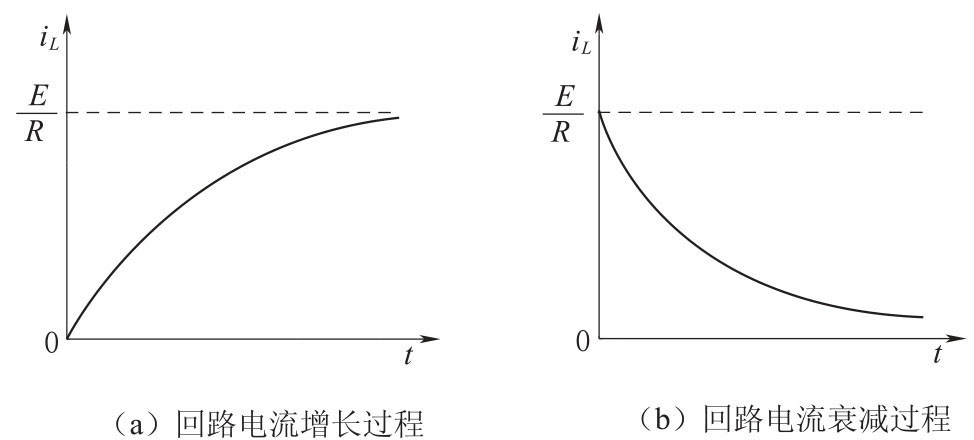
图3-36 回路电流变化过程
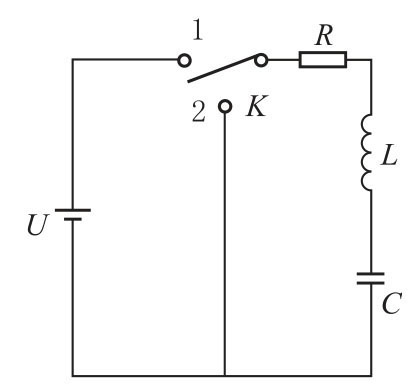
图3-37 串联RLC 电路
对上式求微分得
放电过程：当电容器被充电到U 时，将开关K 从位置1打到位置2，则电容器在闭合的RLC 回路中进行放电。此时回路方程为
令
，λ 称为电路的阻尼系数，那么由充放电过程的初始条件：充电，t=0时，i=0，uC=0；放电t=0时，i=0，uC=U，方程（3-33）、方程（3-34）的解可以有三种形式：
（1）阻尼较小时，λ＜1，即
，有
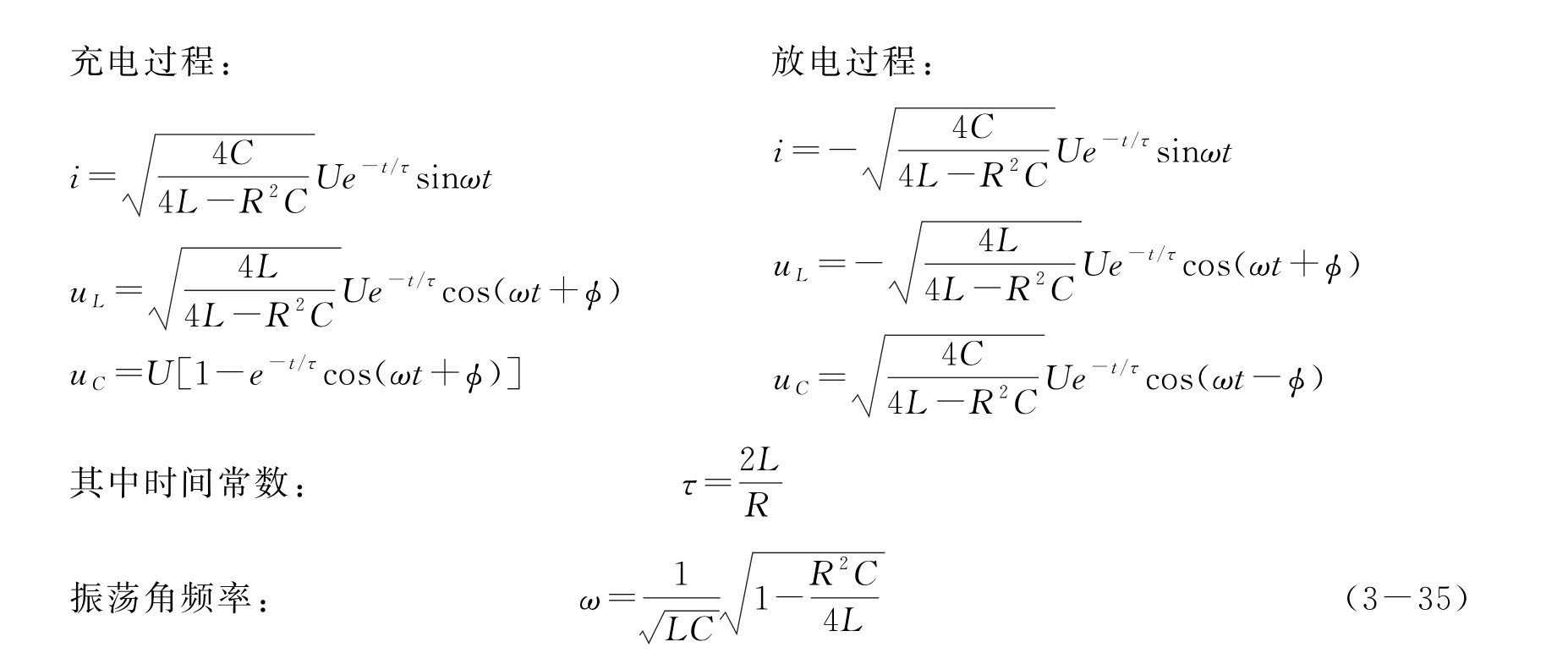
由上述各式可知，电路中的电压、电流均按正弦律作衰减（或称欠阻尼）振荡状态。如图3-38中的曲线a 所示的周期性衰减振荡曲线。
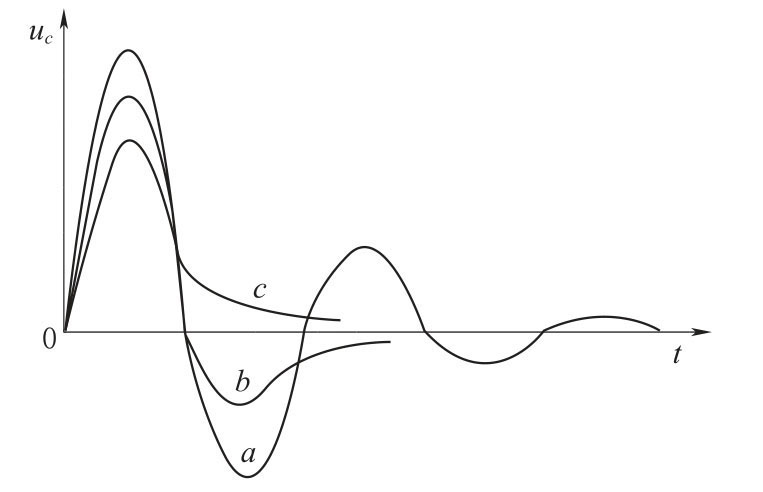
图3-38 RLC 电路对阶跃电压的响应
（2）临界阻尼状态，当λ=1时，即
，此时方程的解如下。
由上各式可见，此时电路中各物理量的变化过程不再具有周期性，振荡状态如图3-38中曲线b 所示，这时的电阻值称为临界阻尼电阻。
（3）过阻尼状态，λ＞1，即
，方程的解如下。
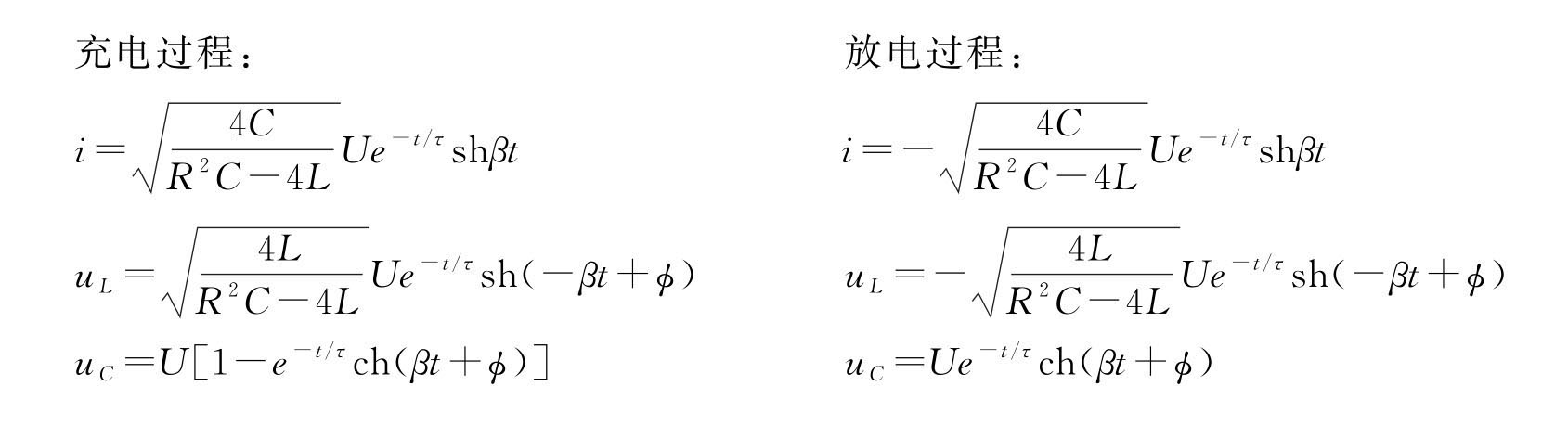
式中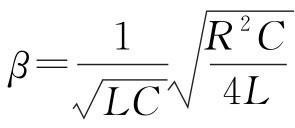
，此时为阻尼较大的情况，此时电路的电压电流不再具有周期性变化的规律，而是缓慢地趋向平衡值，且变化率比临界阻尼时的变化率要小（图3-38中曲线c）。