【实验原理】
光电效应的实验示意图如图3-1所示,图中GD 是光电管,K 是光电管阴极,A 为光电管阳极,G 为微电流计,V 为电压表,E 为电源,R 为滑线变阻器,调节R 可以得到实验所需要的加速电位差UAK。光电管的A、K 之间可获得电压从-U 到0再到+U 连续变化的电压。实验时用的单色光是从低压汞灯光谱中用干涉滤色片过滤得到的,其波长分别为365nm、405nm、436nm、546nm、577nm。无光照阴极时,由于阳极和阴极是断路的,所以G 中无电流通过。用光照射阴极时,由于阴极释放出电子而形成阴极光电流(简称阴极电流)。加速电位差UAK越大,阴极电流也越大,当UAK增加到一定数值后,阴极电流不再增大而达到某一饱和值IH,IH的大小和照射光的强度成正比,如图3-2所示。加速电位差UAK变为负值时,阴极电流会迅速减小,当加速电位差UAK负值到一定数值时,阴极电流变为“0”,与此对应的电位差称为遏止电位差。这一电位差用Ua来表示。|Ua|的大小与光的强度无关,而是随着照射光的频率增大而增大(图3-3)。
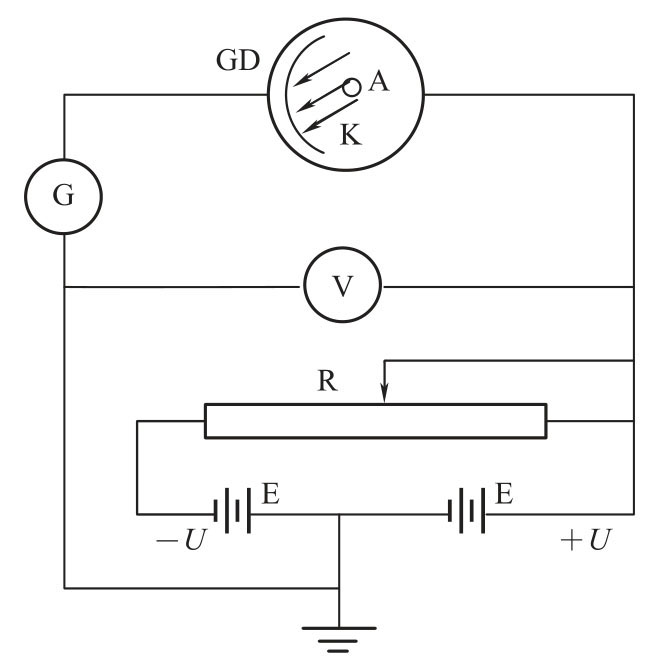
图3-1 光电效应实验示意图
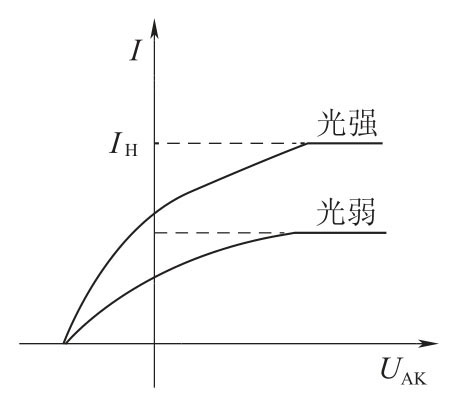
图3-2 光电管的伏-安特性
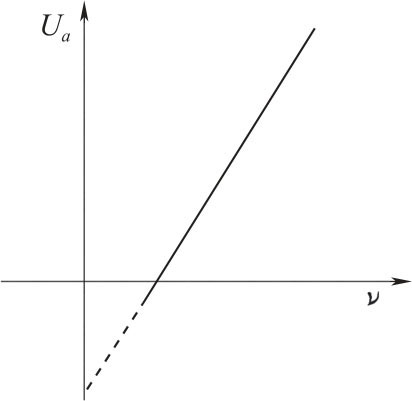
图3-3 光电管遏止电位的频率特性
(1)饱和电流的大小与光的强度成正比。
(2)光电子从阴极逸出时具有初动能,其最大值等于它反抗电场力所做的功,即
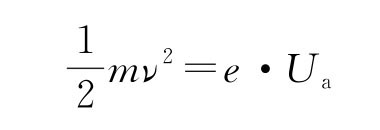
因为Ua∝ν,所示初动能大小与光的强度无关,只是随着频率的增大而增大。Ua∝ν 的关系可用爱因斯坦方程表示如下:

实验时用不同频率的单色光(ν1、ν2、ν3、ν4、…)照射阴极,测出相对应的遏止电位差(Ua1、Ua2、Ua3、Ua4、…),然后作出Ua~ν 图,由此图的斜率即可以求出h。
(3)如果光子的能量hν≤W 时,无论用多强的光照射,都不可能逸出光电子。与此相对应的光的频率则称为阴极的红限,且用![]() 来表示。实验时可以从Ua~ν 图的截距求得阴极的红限和逸出功。
来表示。实验时可以从Ua~ν 图的截距求得阴极的红限和逸出功。
本实验的关键是正确确定遏止电位差,作出Ua~ν 图。至于在实际测量中如何正确地确定遏止电位差,还必须根据所使用的光电管来决定。下面就专门对如何确定遏止电位差的问题作简要的分析与讨论。
如果使用的光电管对可见光都比较灵敏,则暗电流也很小。由于阳极包围着阴极,即使加速电位差为负值时,阴极发射的光电子仍能大部分射到阳极。而阳极材料的逸出功又很高,可见光照射时是不会发射光电子的,其电流特性曲线如图3-4所示。图中电流为零时的电位就是遏止电位差Ua。
然而,光电管在制造过程中,工艺上很难保证阳极不被阴极材料所污染(这里污染的含义是阴极表面的低逸出功材料溅射到阳极上),而且这种污染还会在光电管的使用过程中日趋加重。被污染后的阳极逸出功降低,当从阴极反射过来的散射光照到它时,便会发射出光电子而形成阳极光电流。实验中测得的电流特性曲线,是阳极光电流和阴极光电流迭加的结果,如图3-5的实线所示。
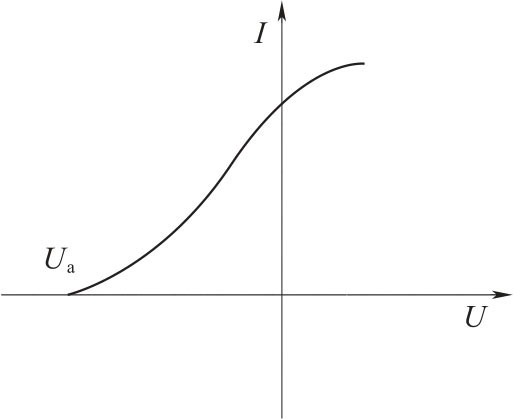
图3-4 光电管电流特性曲线
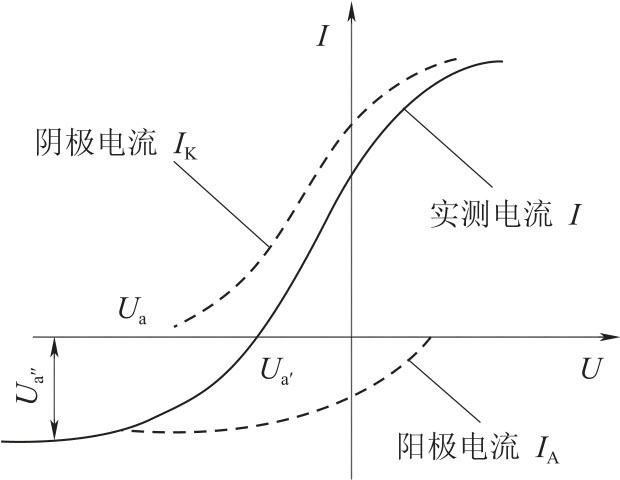
图3-5 遏止电位差确定
由图3-5可见,由于阳极的污染,实验时出现了反向电流。特性曲线与横轴交点的电流虽然等于“0”,但阴极光电流并不等于“0”,交点的电位差Ua也不等于遏止电位差Ua。两者之差由阴极电流上升的快慢和阳极电流的大小所决定。如果阴极电流上升越快,阳极电流越小,U'a与Ua之差也越小。从实际测量的电流曲线上看,正向电流上升越快,反向电流越小,则U'a与Ua之差也越小。
由图3-5可以看到,由于电极结构等种种原因,实际上阳极电流往往饱和缓慢,在加速电位差降到Ua时 ,阳极电流仍未达到饱和,所以反向电流刚开始饱和的拐点电位差U″a也不等于遏止电位差Ua。两者之差视阳极电流的饱和快慢而异。阳极电流饱和得越快,两者之差越小。若在负电压增至Ua之前阳极电流已经饱和,则拐点电位差就是遏止电位差Ua。
总而言之,对于不同的光电管应该根据其电流特性曲线的不同采用不同的方法来确定其遏止电位差。假如光电流特性的正向电流上升得很快,反向电流很小,则可以用光电流特性曲线与暗电流特性曲线交点的电位差U'a近似地当作遏止电位差Ua(交点法)。若反向特性曲线的反向电流虽然较大,但其饱和速度很快,则可用反向电流开始饱和时的拐点电位差U″a当作遏止电位差Ua(拐点法)。
