有效数字及运算
1.有效数字概念
测量总伴随着误差,它的值不能无止境地写下去。例如,用米尺测量某一物体长度,测得长度读数7.26cm,显然7.2是准确数字,而6是可疑数字;又如某长方体体积计算值V=112.3456cm3,不确定度ΔV=0.5cm3,小数点后第一位3已是可疑数字,这样V 的最后三位数456没有意义,结果表示为V=(112.3±0.5)cm3,这样包含准确数字和一位可疑数字称有效数字。测量结果应该用有效数字表示。
(1)有效数字位数。如0.507、0.0753、5.73×104是三位有效数字,0.5730、0.5703是四位有效数字。小数点后首位非零数字之前的零不计入有效数字位数。在十进制单位换算中,只涉及小数点位置改变,而不允许改变有效位数。例如5.6m 为两位有效数字,在换算成km 或mm 时应写为
而5.6m=5600mm 的写法是错的。
(2)有效数字位数由测量仪器决定。测量仪器精度越高,测量数据有效数字位数也越多。如分别用米尺、游标卡尺、千分尺测长度为16.4762mm 某物体,记数分别为16.5mm、16.48mm、16.476mm。
2.有效数字与不确定度
在前面(三)部分,我们要求所有测量结果必须表示成测量值=最佳估计值±不确定度(单位)的形式,其中的最佳估计值的有效数字按照下述“有效数字的运算规则”来确定。而不确定的有效数字规定如下:
不确定度(相对不确定度)一般取一位有效数字,首位是1或2应取二位有效数字。在例题1-1中:用千分尺对一钢丝直径d 进行测量,最后计算出的不确定度![]()
![]() ,由于计算结果0.0046首位为4,并非1或2,所以只能保留一位有效数字,即写成0.005。 当然如果这里Δd计算结果为0.0223,这时由于首位为2,则其不确定度Δd=0.0223≈0.023,此时取二位有效数字。注意一点:对于不确定度,其有效数字只进不舍,如Δx=0.042≈0.05,以确保结果的可靠性。最后的结果表达式,即:测量值=最佳估计值±不确定度(单位),其最佳估计值和不确定度的有效数字按照上述所说确定。其结果表达式应该遵循:最佳估计值有效数字末位应与不确定度的末位对齐。
,由于计算结果0.0046首位为4,并非1或2,所以只能保留一位有效数字,即写成0.005。 当然如果这里Δd计算结果为0.0223,这时由于首位为2,则其不确定度Δd=0.0223≈0.023,此时取二位有效数字。注意一点:对于不确定度,其有效数字只进不舍,如Δx=0.042≈0.05,以确保结果的可靠性。最后的结果表达式,即:测量值=最佳估计值±不确定度(单位),其最佳估计值和不确定度的有效数字按照上述所说确定。其结果表达式应该遵循:最佳估计值有效数字末位应与不确定度的末位对齐。
用不确定度表示的测量结果正确形式应该如:(157.6±0.3)g、(7.386±0.007)mm、(979.35±0.25)cm/s2、(115.80±0.19)cm3;而(157.26±0.3)g、(157.6±0.13)等都是不规范的形式。相对不确定度如:0.15%、0.6%、0.23%、0.3%,取一或二位有效数字。
3.有效数字尾数修约法则(四舍六入五凑偶,而非四舍五入)
(1)要保留有效数字末位的那个数如果大于等于6则进位;如果小于等于4则舍去。
(2)紧跟要保留有效数字末位的那个数如果是5,5后面有不为零的数,则进位;5后面数全为零或没有数,则看要保留有效数字末位的那个数,若是奇数进位;偶数(包括0)不进位。
如:将下面数保留四位有效数字。
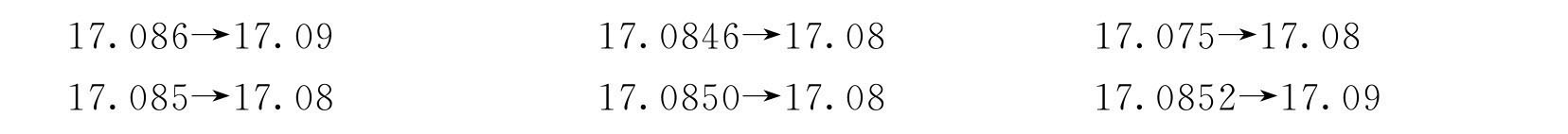
4.有效数字的运算规则(https://www.daowen.com)
运算时应使结果具有足够的有效数字,不要少算,也不要多算。少算会带来附加误差,降低结果精度;多算没有必要,算的位数很多,但绝不可能减少误差。
有效数字运算取舍的原则是:运算结果保留一位可疑数字。
(1)加、减运算。
结论:诸量相加(相减)时,其和(差)值在小数点后所应保留的位数与诸数中小数点后位数最少的一个相同。
(2)乘、除运算。
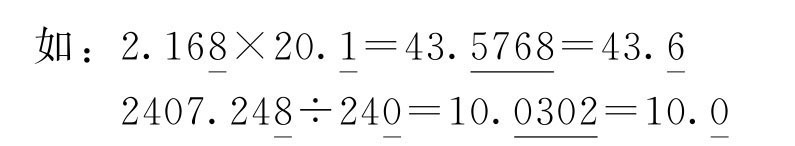
结论:诸量相乘(除)后其积(商)所保留的有效数字,只需与诸因子中有效数字最少的一个相同。
(3)乘方、开方的有效数字与其底的有效数字相同。
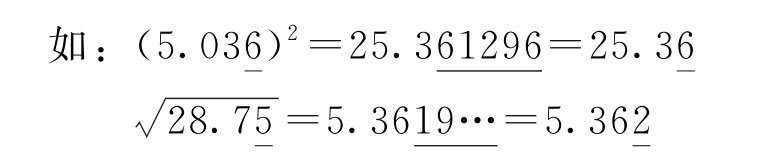
(4)对数函数、指数函数和三角函数运算结果的有效数字必须按照不确定度传递公式来决定(通过例1-4说明)。
(5)无理常数π,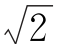 ,…,计算过程中这些常数项参加运算时,其取的位数应比测量数据中位数最少者多取一位。例:计算圆面积公式S=πR2,圆半径R=5.60cm,应取π=3.142,则S=17.6cm2。
,…,计算过程中这些常数项参加运算时,其取的位数应比测量数据中位数最少者多取一位。例:计算圆面积公式S=πR2,圆半径R=5.60cm,应取π=3.142,则S=17.6cm2。
例1-4 已知x=200.0±0.2,θ=60.0°±0.03°,试求:
(1)y=lnx。(2)![]() 。(3)y=sinθ。
。(3)y=sinθ。
解:(1)y=ln200.0=5.298317367(由函数型计算器给出)。
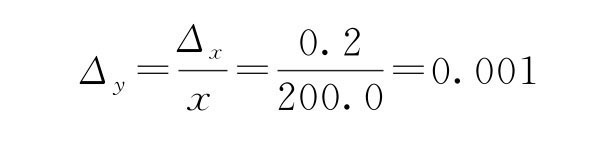
ln200.0应取三位小数,即ln200.0=5.298。

(3)y=sin60.00°=0.866025403(由函数型计算器给出)。
sin60.00°应取四位小数,即sin60.00°=0.8660。
应该指出,有效数字位数取决于测量,并非运算过程。我们不能任意增加有效数字位数。同学们最容易犯的一个错误就是在计算过程中,随意增减计算结果的有效数字。例如用米尺测量某物体长度两次结果分别为1.10cm和1.11cm,则其同学们在计算平均值时一般就直接给出结果![]() ;这是错误的,按照上述规则,最后的平均值应该是1.10cm。目前普遍使用函数型计算器进行计算,一般可显示10位有效数字,实际计算时并不需要那么多,应由有效数字的运算规则合理取舍。但也不能人为减少有效数字,以确保计算的可靠性。
;这是错误的,按照上述规则,最后的平均值应该是1.10cm。目前普遍使用函数型计算器进行计算,一般可显示10位有效数字,实际计算时并不需要那么多,应由有效数字的运算规则合理取舍。但也不能人为减少有效数字,以确保计算的可靠性。
