【实验原理】
1.非线性电路与非线性动力学
实验电路如图3-19所示,图中只有一个非线性元件R,它是一个有源非线性负阻器件。电感器L 和电容器C2组成一个损耗可以忽略的谐振回路;可变电阻R0和电容器C1串联将振荡器产生的正弦信号移相输出。本实验所用的非线性元件R 是一个五段分段线性元件。
图3-20所示的是该电阻的伏-安特性曲线,可以看出加在此非线性元件上电压与通过它的电流极性是相反的。由于加在此元件上的电压增加时,通过它的电流却减小,因而将此元件称为非线性负阻元件。
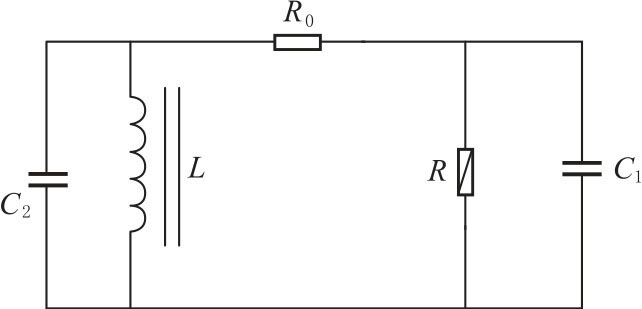
图3-19 非线性电路原理图
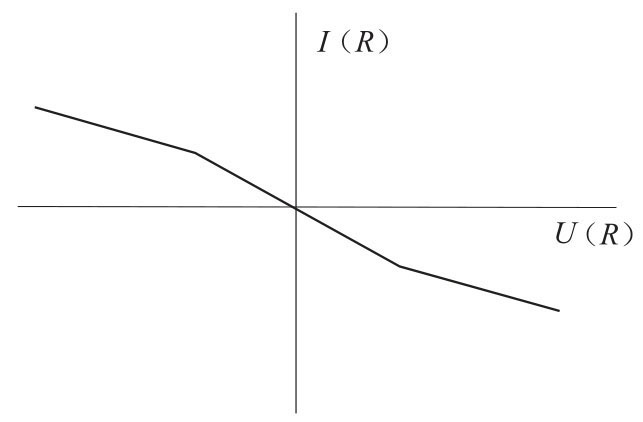
图3-20 非线性元件伏-安特性
图3-19电路的非线性动力学方程为
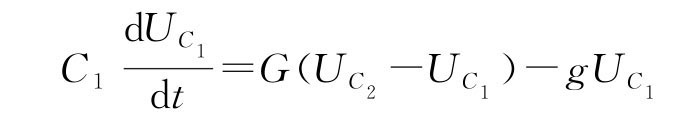
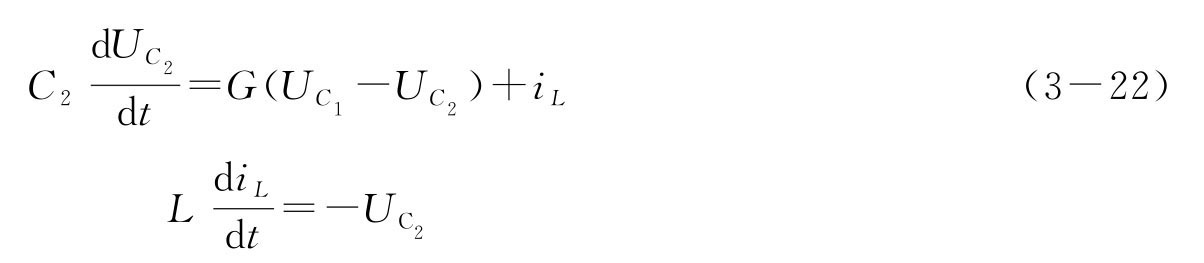
式中:UC1、UC2为C1、C2上的电压;iL为电感L 上的电流;G=1/R0为电导。
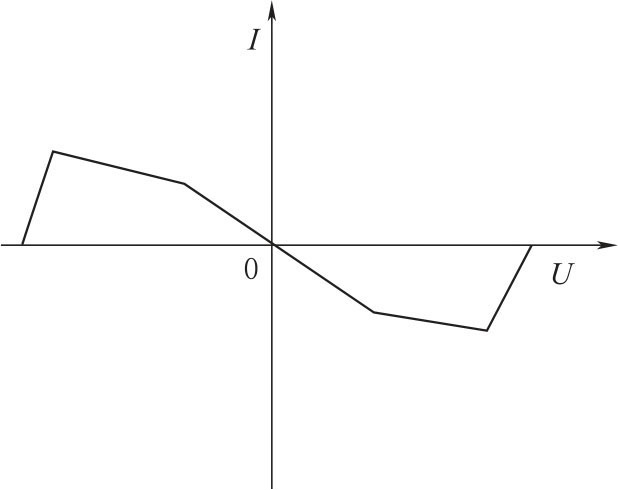
图3-21 双运算放大器非线性元件的伏-安特性
在图3-19 中,g 为U 的函数,如果R 是线性的,g 是常数,电路就是一般的振荡电路,得到的解是正弦函数,电阻R0的作用是调节C1和C2的位相差,把C1和C2两端的电压分别输入到示波器的x 轴、y 轴,则显示的图形是椭圆。如果R 是非线性的,会看到什么现象呢?
电路中的R 是非线性元件,它的伏-安特性如图3-21所示,是一个分端线性的电阻,整体呈现出非线性。gUC1是一个分段线性函数。由于g 总体是非线性函数,三元非线性方程组(3-22)没有解析解。若用计算机编程进行数据计算,当取适当电路参数时,可在显示屏上观察到模拟实验的混沌现象。
除了计算机数学模拟方法之外,更直接的方法是用示波器来观察混沌现象,实验电路如图3-22所示,非线性电阻是电路的关键,它是通过一个双运算放大器和六个电阻组合来实现的。电路中,LC并联构成振荡电路,R0的作用是分相,使J1和J2两处输入示波器的信号产生位相差,可得到x,y 两个信号的合成图形,双运算放大器LF353的前级和后级正、负反馈同时存在,正反馈的强弱与比值R3/R0、R6/R0有关,负反馈的强弱与比值R2/R1、R5/R4有关。当正反馈大于负反馈时,振荡电路才能维持振荡。若调节R0,正反馈就会发生变化,LF353处于振荡状态,表现出非线性,LF353与六个电阻等效于一个非线性电阻,它的伏-安特性大致如图3-21所示。
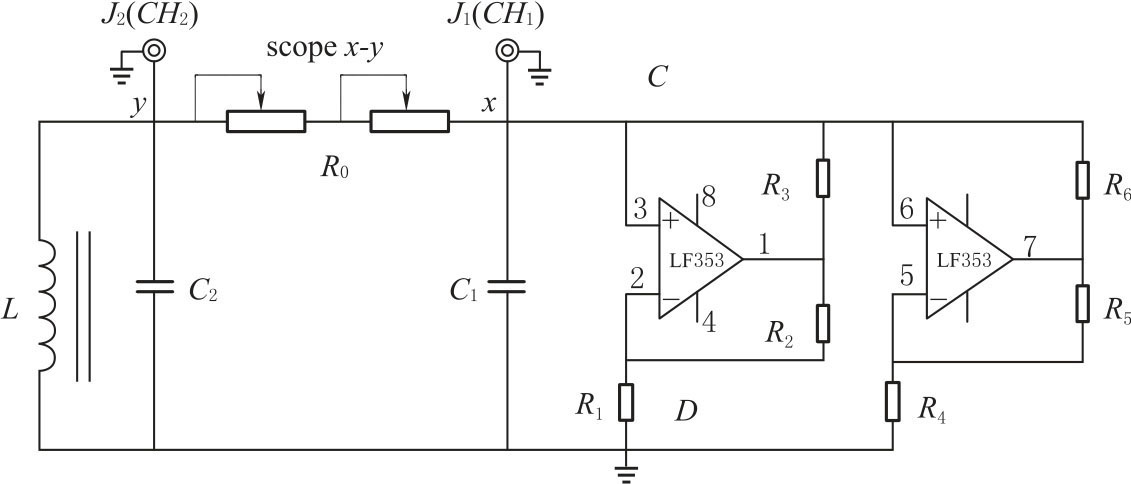
图3-22 非线性电路混沌实验电路
2.有源非线性负阻元件的实现
有源非线性负阻元件实现的方法有很多种,这里使用的是一种较简单的电路,采用两个运算放大器(一个双运算放大器LF353)和六个配制电阻来实现,其电路如图3-23所示,它的伏安特性曲线如图3-21所示,实验所要研究的是该非线性元件对整个电路的影响,而非线性负阻元件的作用是使振动周期产生分岔和混沌等一系列非线性现象。从大到小改变R0,可观察到如图3-24 所示的周期分岔和双吸引子等混沌现象。实际非线性混沌实验电路如图3-22所示。
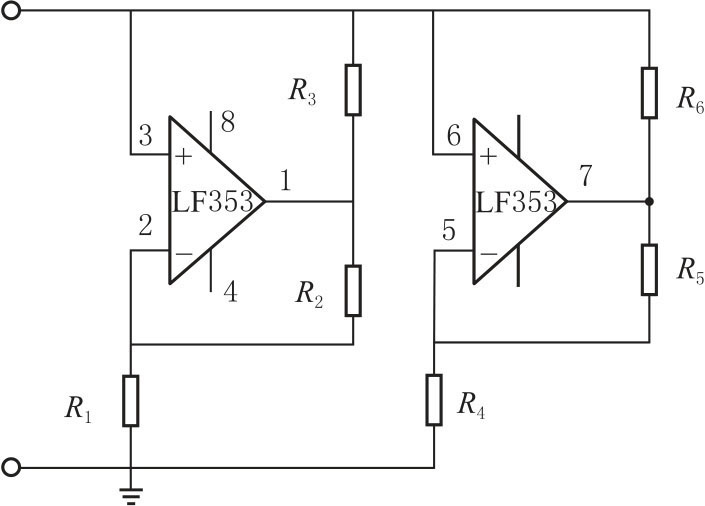
图3-23 有源非线性器件
