【实验原理】
当截面为S,长度为L0的棒状(或线状)材料,受拉力F 拉伸时,伸长了ΔL,其单位面积截面所受到的拉力F/S 称为应力,而单位长度的伸长量ΔL/L0称为应变。根据胡克定律,在弹性形变范围内,棒状(或线状)固体所受应力与它的应变成正比:
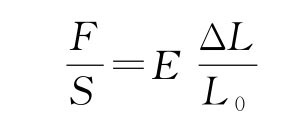
其比例系数E 取决于固体材料的性质,称为杨氏弹性模量。

本实验是测定某一种型号钢丝的杨氏弹性模量,其中F、S、L0都可用常规的测量方法测量,但ΔL 却难以用常规的方法精确测定,故采用“光杠杆”放大法来测定这一微小的长度改变量ΔL。
图2-1所示为光杠杆测微小长度变化的原理图。图2-2所示为光杠杆镜示意图,图2-3所示为杨氏模量实验仪器(主要部分)。其中G 是光杠杆镜。图2-1中b 是光杠杆常数,就是光杠杆镜后足尖到前两足尖连线的距离,即三足尖连线形成等腰三角形的高。光杠杆镜后足尖置于夹紧钢丝的圆柱体B上,并且B刚好悬在C台圆孔中间(图2-3),光杠杆镜后足尖随被测钢丝的伸长、缩短而下降、上升,从而改变了杠杆镜面法线的方向,使得钢丝原长为L0时,位于图右侧的望远镜从杠杆镜面中看到的读数为n1;而钢丝受力伸长后光杠杆镜的位置变为虚线所示,此时望远镜上的读数则为n2。这样,钢丝的微小伸长量ΔL,对应有光杠杆镜的角度变化量θ,而对应的读数变化则为Δn=n1-n2。从图2-1中可见:(https://www.daowen.com)

将式(2-2)和式(2-3)联立后得式中Δn=|n2-n1|,其中D 是置于平台C上光杠杆镜镜面到标尺的距离,如图2-1所示。由于D≫b,所以Δn≫ΔL,从而获得对微小量的线性放大,提高了ΔL 的测量精度,这被称为放大法。
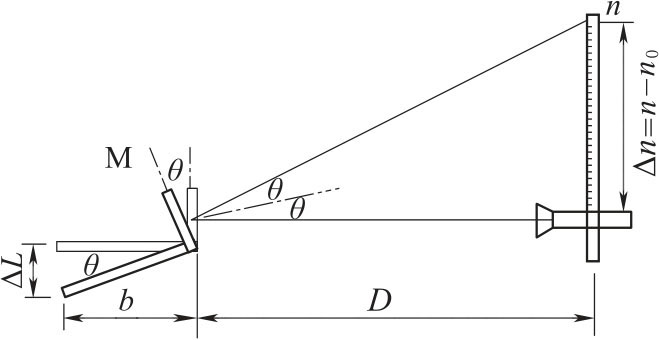
图2-1 光杠杆原理
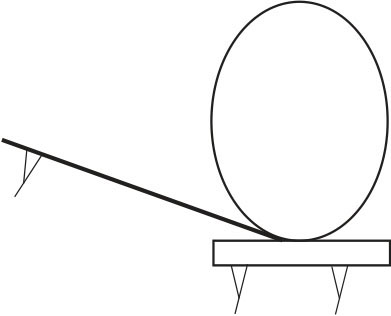
图2-2 光杠杆镜
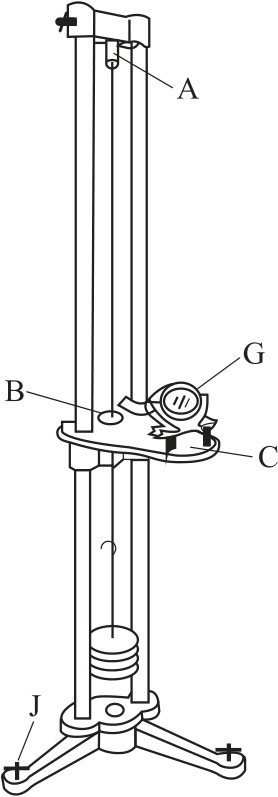
图2-3 杨氏模量仪
鉴于金属受外力时存在着弹性滞后效应,即钢丝受到拉伸力作用时,并不能立即伸长到应有的长度Li(Li=L0+ΔLi),而只能伸长到Li-δLi。同样,当钢丝受到的拉伸力一旦减小时,也不能马上缩短到应有的长度Li,仅缩短到Li+δLi。因此,为了消除弹性滞后效应引起的系统误差,测量中应包括增加拉伸力以及对应地减少拉伸力这一对称测量过程。因为只要将相应的增、减测量值取平均,就可以消除滞后量δLi的影响。
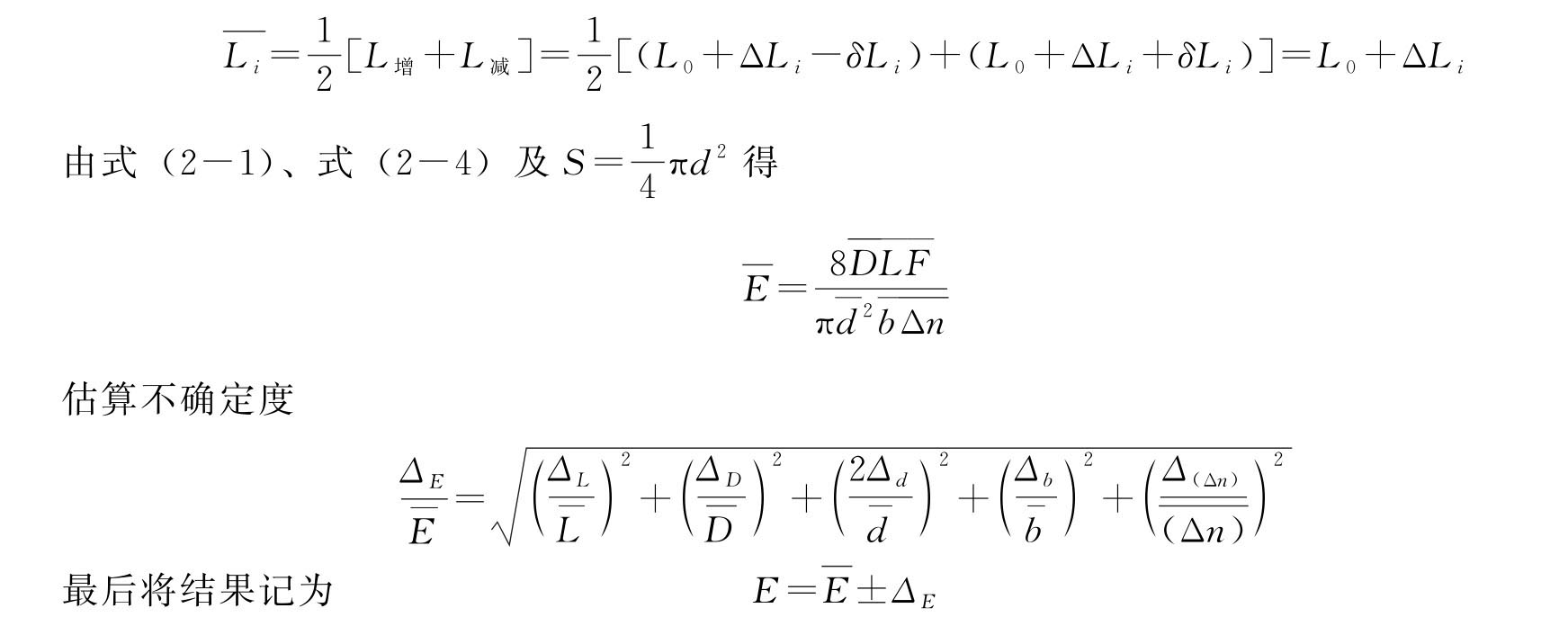
杨氏弹性模量单位为N/m2。
