分配数列的编制
根据分组标志性质的不同,分配数列可分为品质数列和变量数列。
(一)品质数列
品质数列是按品质标志分组的数列,用来观察总体单位中不同属性的单位分布情况,即将总体的所有单位按属性归类整理形成的分配数列。
品质数列由各组名称和次数组成。各组次数可以用绝对数表示,即频数,也可以用相对数表示。
【例3-1】 为研究某生产基地职工的文化程度情况,调查者随机调查了50 名职工,情况如表3-2 所示。
表3-2 某生产基地职工情况
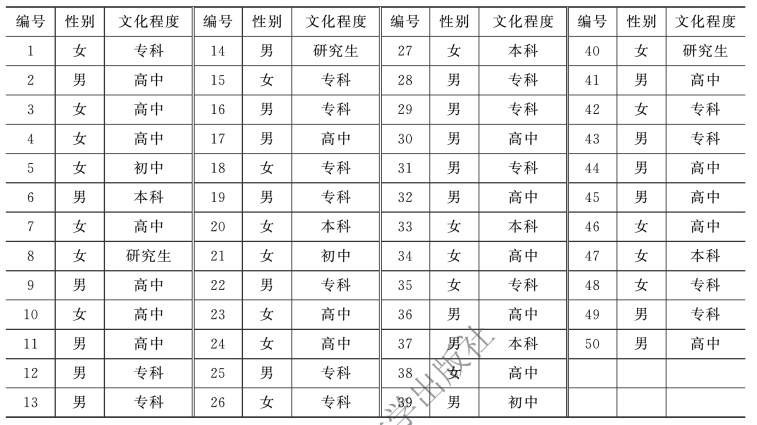
解 表3-2 中给出了性别、文化程度信息,按文化程度分组、归类,如图3-3 所示。
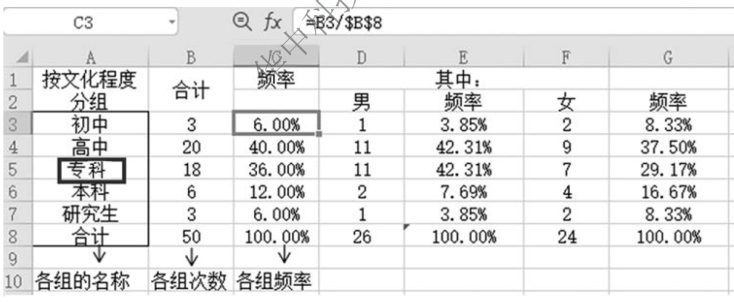
图3-3 按文化程度分组统计
品质数列一般比较稳定,通常能准确地反映总体的分布特征,但要注意分组时,应包括分组标志的所有表现,不能有遗漏,且各种表现相互独立,不得相融。
(二)变量数列
变量数列是将总体按数量标志分组,将分组后形成的各组变量值与该组中所分配的单位次数或频数,按照一定的顺序相应排列所形成的分配数列。这种情况下,数量标志的变异性体现在它自身不断变动的数量上,故称为变量数列。
按数量标志分组,根据数量标志的性质与数据的变异大小,可将变量数列分为单项式变量数列和组距式变量数列两种。
1.单项式变量数列
单项式变量数列是将变量值相同的单位归为一组,即一个变量值作为一组,并按照一定顺序排列形成的变量数列。
单项式变量数列由各组名称(由变量值表示)和次数(或频率)组成。频率大小表明各组标志值对总体的相对作用程度,也表明各组标志值出现的概率大小。
对于离散变量且变量不同的取值个数较少时,宜采用单项式变量数列。
【例3-2】 已知某单位50 名员工家庭人口资料如下:
2 3 4 4 3 1 2 5 3 2 1 2 2 2 3 2 3 3 4 5 2 3 2 4 3
2 3 4 1 3 2 1 3 2 3 3 5 3 2 1 2 4 3 1 2 5 3 2 1 3
要求:根据以上资料编制变量数列。
解 从资料中看出,家庭人口数量变动范围较小,最少的为1 人,最大的为5 人,宜编制出单项式变量数列,按数值归类,将数值相同的归为一组,排序列表。
变量一般用符号x 表示,变量的具体数值(即变量值)一般用符号xi 表示;单位数(即次数)一般用f 表示,意思是在所有数据中某个数据出现的次数,各组次数或频数通常用符号fi表示。编制的变量数列如图3-4 所示。
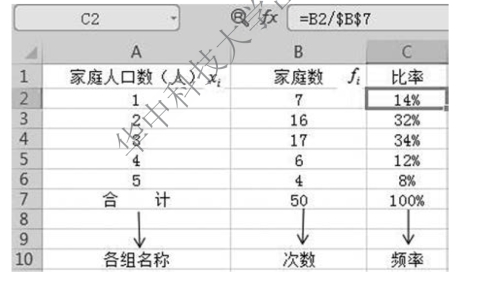
图3-4 员工家庭人口变量数列
单项式变量数列的编制比较明确、容易。但是,用连续变量分组来编制分配数列,或者虽是离散变量,但数值很多、变化范围很大时,变量值不能一一列举,单项式变量数列就不适用了,需要将变量进行合并,可采用组距式变量数列的形式。
2.组距式变量数列
组距式变量数列指数列中的各个组是由表示一定变动范围的两个数值所组成的,适用于连续变量或者变量值个数较多、变动范围较大的离散变量,由于不受变量数值的多少和变异范围大小的限制,应用较为广泛。
组距式变量数列又分以下类型:
(1)根据组距是否相等,分为等距式变量数列和异距式变量数列。
①等距式变量数列中各组组距是相等的,适用于现象性质差异的变动比较均衡或标志变异比较均匀的情况。由于其各组组距相等,消除了组距影响,各组次数的分布不受组距大小的影响,一般呈正态分布。
②异距式变量数列中的组距是不全相等的,又称不等距分组,用于那些分布存在明显的偏斜倾向以及标志变异范围较大或呈比例关系变化的现象。采用异距式变量数列能比较准确地反映总体内部各组成部分的性质差异。
例如,进行2019 年末人口统计时,为了说明劳动年龄人口与非劳动年龄人口之比,将人口按年龄分组,显然劳动年龄人口范围要比非劳动年龄人口范围大,采用不等距分组更为合理,如表3-3 所示。
表3-3 2019 年末人口统计
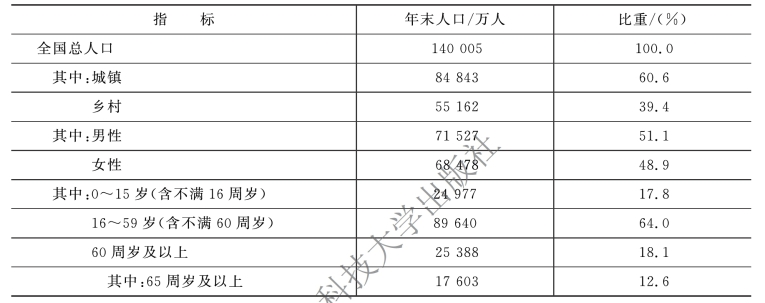
注:资料来源于2019 年统计公报。
又如,某钢铁厂高炉按容积(以m3 计)分组,分为“100 以下”“100~200”“200~400”“400~800”“800~1600”“1600”以上,显然,各组组距呈比例关系。
在组距式变量数列中,表示各组界限的变量值称为组限,其中较小的变量值称为下限,用L表示,较大的变量值称为上限,用U 表示,各组上限与下限之差即为组距,用d 表示;各组上限与下限的中点称为组中值。
组限、组距与组中值的关系为:

组中值具有一定的假定性,即假定次数在各组内的分布是均匀的,组中值是一个近似值,代表了各组内的一般水平。
(2)根据组限是否齐全,分为闭口组与开口组。
如果各组的组限都齐全,这样的组距式变量数列称为闭口组。闭口组的第一组的下限应小于或等于最小的数据,最后一组的上限应大于最大的数据,以便将所有数据包括在内。
如果组限不齐全,这样的组距式变量数列称为开口组,即最小的组缺下限或最大的组缺上限,表现形式为“××以上”“××以下”,主要用于出现极端值的现象。为了避免空白组出现,常用开口组。
例如,在人的身高分布中,2 米以下可按等距分组,2 米以上范围大,人数少,可采用开口组。对于缺少上限数值或下限数值的开口组,计算组中值时可假定该组的次数与相邻组的次数一致或最接近。
对于缺少下限数值的组,组中值的计算公式为:
![]()
对于缺少上限数值的组,组中值的计算公式为:

(3)按变量性质分,分为离散型变量数列与连续型变量数列。
①对于离散型变量数列,由于离散变量可以一一列举,故其组限设置可以是重叠的,也可以是不重叠的。如某地区将企业按职工人数分组:100 人以下;101~500 人;501~5000 人;5000人以上。
由于离散变量各变量值之间以整数断开,变量值之间有明显的界限,上下限都可以用准确的数值表示,组限非常清楚。
②由于连续型变量数列各变量值之间可做无限分割,有小数存在,上下限不能用两个确定的值表示,只能将前一组的上限与本组的下限用同一数值表示。
对于连续型变量数列,在确定组限与单位数时,有一原则可循,即“上组限不在内”原则:各组只包括本组下限变量值的单位,不包括本组上限变量值的单位。
实际统计工作中,虽然变量区分连续变量与离散变量,但为了计算、绘图等的方便,保证整体单位不出现重复、遗漏,可采用连续型变量数列的形式代替离散型变量数列。
