抽样推断中的基本概念
（一）全及总体和样本总体
在抽样推断中，存在两个不同的总体，即全及总体和样本总体。
1.全及总体
抽样调查所要认识对象的全体，叫全及总体，也叫母体，简称总体，它是具有某种共同性质或特征的许多单位的集合体。全及总体的单位数通常用N 来表示。
对于一个总体来说，若被研究的标志是品质标志，则将这个总体称为属性总体，如研究性别差异时的新生婴儿总体，研究设备完好情况时的设备总体。若被研究的标志是数量标志，则将这个总体称为变量总体，如反映体重、身高时的学生总体，反映工资高低时的企业职工总体等。
抽样调查首先要弄清全及总体的范围、单位的含义，构成明确的抽样框，作为抽样的母体。对于一定的问题，全及总体是唯一的、确定的。
2.样本总体
样本总体又叫子样或抽样总体，简称样本。它是从全及总体中随机抽取出来，代表全及总体的那部分单位的集合体。
样本总体的单位数称为样本容量，通常用n 表示，相对N 来说，n 是很小的数，它可以是N的几十分之一、几百分之一、几千分之一、几万分之一等。以很小的样本来推断很大的总体，这是抽样调查法的重要特点。一般来说，单位数达到或超过30 个的样本称为大样本，而单位数在30 个以下的称为小样本。n/N 称为抽样比。社会经济统计的抽样推断多属于大样本；科学实验的抽样多属于小样本。
例如，在100 万户居民中，随机抽取10000 户居民进行家庭收支情况调查，100 万户居民就是全及总体，而被抽中的10000 户居民则构成抽样总体。
需要指出的是，总体是确定的、唯一的，但总体中可供抽取的样本不止一个，在没有抽中之前，任何一个待选样本都有被抽到的可能。
（二）总体参数和样本统计量
在抽样推断调查中，存在两个总体，必然会涉及两套指标。
1.全及指标
反映全及总体数量特征的指标称为全及指标，是根据全及总体各个单位的标志值或标志特征所计算的反映总体某种属性的综合指标，又称总体参数。总体参数是确定的值，却是未知的，需要用样本指标来估计。抽样推断中要用到两个参数，一个是反映总体各单位分布的集中趋势值（平均数），另一个是反映总体分布的离散趋势值，这两个参数就是总体的均值和方差。不同性质的总体需要计算不同的参数。
（1）对于变量总体，设总体中有N 个单位，某项标志的标志值分别为X1，X2，X3，…，XN，权数为FI，则根据资料是否分组有不同的计算方法。
①未分组资料：
总体平均数用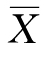
表示：
总体方差用
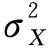表示：
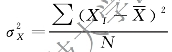
总体标准差用σX 表示：
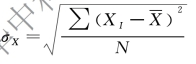
②分组资料：
总体平均数：
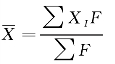
总体方差：
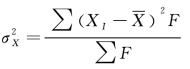
总体标准差：
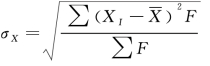
（2）对于属性总体，设总体中具有某种属性的有N1 个单位，不具有某种属性的有N0 个单位，则有如下计算方法。
①总体成数：
②总体是非标志的标准差：
③总体是非标志的方差：
2.抽样指标
抽样指标指根据抽样总体各个单位的标志值或标志特征计算的综合指标，又被称为样本统计量，它是随机变量，随样本的不同而变化。样本统计量一方面表示样本本身的分布状况和特征，另一方面也是总体参数的估计量。样本单位被抽出来以后，就需要计算样本统计量。
（1）对于变量总体，设样本中n 个样本单位某项标志的标志值分别为x1，x2，x3，…，xn-1，xn，权数为fi，根据资料是否分组，有不同的计算方法。
①未分组资料：
样本平均数（又叫样本均值），用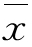
表示：
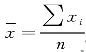
样本方差：
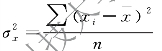
样本标准差：
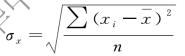
②分组资料：
样本平均数：
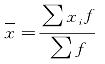
样本方差：
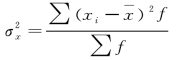
样本标准差：
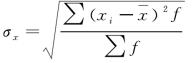
（2）对于属性总体，设总体中具有和不具有某种属性的样本单位数目分别为n1 和n0，则样本统计量有如下计算方法。
①样本成数：
②样本单位是非标志的方差：
③样本单位是非标志的标准差：
（三）抽样误差
抽样误差是抽样调查特有的一种误差，是纯粹由抽样原因引起的抽样指标与全及指标之间的绝对离差，用数学符号表示为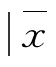
-X|或|p -P|。
抽样误差是抽样调查本身所固有的，当样本容量n 与全及总体单位数N 相等时，抽样调查变成全面调查，抽样误差随之消失。
抽样误差又可分为抽样实际误差与抽样平均误差。
1.抽样实际误差
抽样实际误差是指每次抽样所得的抽样指标与全及指标之间的离差，它随着样本的不同而不同，是一个随机变量，即有多少种可能的样本就有多少种可能的抽样实际误差。因此，在抽样推断中要结合所有可能的样本来研究所有可能的抽样实际误差。
2.抽样平均误差
抽样平均误差是指所有可能出现的样本统计量的标准差。抽样平均误差反映了样本统计量与总体参数的平均离差，也反映了样本统计量对总体参数的代表程度。抽样平均误差越大，样本对总体的代表程度越低；反之，抽样平均误差越小，样本对总体的代表程度越高。
抽样推断是用抽样指标推断全及指标，而推断的依据就是抽样误差。抽样误差虽不能消除，但可以采用一定的方法将其控制在一定范围之内，以保证样本的代表性。