二、平均发展水平
平均发展水平是根据动态数列中各不同时期的发展水平计算出的平均数，又称序时平均数或动态平均数。
动态平均数与一般平均数（静态平均数）虽然都属于平均数，可将研究现象的数量差异抽象化，概括反映现象的一般水平，且都具有平均指标的本质特征——抽象性和代表性，但二者平均的对象不同，计算方法也不同，主要表现在：
第一，一般平均数是根据变量数列计算的；序时平均数是根据时间数列计算的。
第二，一般平均数平均的是总体各单位某一标志值的差异；序时平均数平均的是被研究现象本身的数量在不同时间上的差异。
第三，一般平均数是同一时间总体各单位某个标志值的平均水平；序时平均数是将不同时间的现象水平加以平均得到的平均发展水平。
例如，2013 年某地区农民年人均纯收入为23431 元，2013—2017 人均纯收入为56241 元，前者是将不同农民之间的收入差异予以抽象化，反映全体农民收入的一般水平，后者是将2013年、2014 年、2015 年、2016 年、2017 年各年的收入差异予以抽象化，反映这一段时间的收入发展的一般水平。
序时平均数的计算方法要根据时间序列指标的性质来确定，构成时间数列的指标性质和特点不同，序时平均数的计算方法各不相同。其中，根据总量指标时间数列计算序时平均数是最基本的方法，相对数动态数列和平均数动态数列是由总量指标时间数列派生的，其计算方法最终也要回归对总量指标时间数列的计算。
（一）根据总量指标时间数列计算序时平均数
总量指标时间数列分为时期数列和时点数列两种。
1.由时期数列计算序时平均数
时期数列中的每项均为时期指标数值，是可以相加的，相加以后得到全期的总量，再将全期的总量分摊到每一期，就可以得到时期指标序时平均数，因此，通常采用简单算术平均数方法计算。
设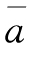
为序时平均数，a1，a2，a3，…，an-1，an 为各期发展水平，n 为时期项数，则
【例8-1】 某企业2011—2016 年不变价格工业总产值如表8-7 所示。要求：计算2011—2016年工业总产值的平均发展水平。
表8-7 某企业2011—2016 年不变价格工业总产值 （单位：万元）
解 计算过程如图8-2 所示。
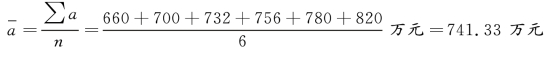
图8-2 2011—2016 年不变价格工业总产值的平均发展水平计算过程
2.由时点数列计算序时平均数
由于时点数列中的数值反映现象在某一时间点上的水平，不能相加、不能求和，只有进行转换，变成可以相加、可以求和的总量才能求平均数。现分几种不同情况加以说明。
（1）根据连续性时点数列计算序时平均数。
若时点数列资料是逐日登记且逐日排列的，这样的时点数列称为连续性时点数列。连续性时点数列中的数值是可以相加的。连续性时点数列有连续性变动和非连续性变动两种情况。
第一种，连续性变动时点数列。
连续性变动时点数列，也称为间隔相等的连续性时点数列，即每日指标数值都进行登记所形成的时间数列。对于这种数列，采用简单平均法计算，用公式表示如下：
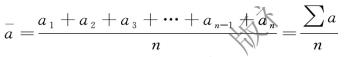
【例8-2】 某股票连续5 个交易日的收盘价格统计数据如表8-8 所示。
表8-8 某股票收盘价格统计数据
要求：计算该股票的平均价格。
解 以上数据形成的是连续性变动时点数列，则
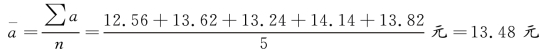
第二种，非连续性变动时点数列。
在实际统计工作中，若现象未发展变动，每天都进行记录是没有必要的。非连续性变动时点数列，也称间隔不等的连续性时点数列，就属于这种情况，形成这种数列的时点资料不是逐日记录的，只是在发生变动时才予以记录。这意味着未记录的这一段时间内的数据与以前记录的数据是相同的，是已知的，如果将数据按日补全，本质仍然是连续性时点数列，因此在计算序时平均数时，采用连续性时点数列计算序时平均数的方法，然后进行简化。这样就形成了以已有的数据为变量、以每次变动持续的时间间隔长度为权数的加权平均数。
设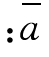
为序时平均数，f 为数据之间的时间间隔长度。
计算公式为：
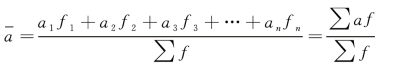
【例8-3】 某企业某月工人人数有如下记录：1 日共有工人218 人，11 日18 人辞职，16 日招聘6 人，25 日又有9 人辞职，其余时间人数未变。
要求：计算该单位该月份平均工人人数（按30 天计算）。
解 已知资料表明：从1日至10日这10 天都是218人，人数未发生变动，218人持续时间为10 天；11日至15日都是200人（218人-18人），持续的时间为5 天；16日至24日每天人数为206人（200 人+6人），持续的时间为9天；1月25日至月底人数为197人（206人-9人），持续时间为6 天。这样，每天人数都是已知的，由非连续性变动时点数列变为连续性时点数列。将资料进行整理，如图8-3 所示。
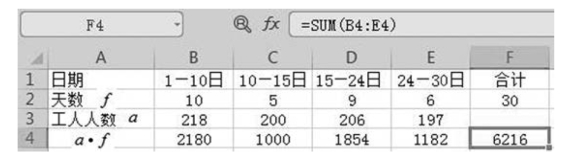
图8-3 月工人人数统计资料
该企业该月份平均工人人数为：
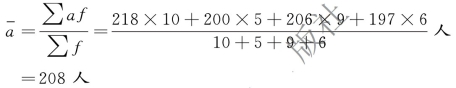
（2）根据间断时点数列计算序时平均数。
间断时点数列分为两种情况，一种是间隔相等的，一种是间隔不等的。
第一种，间隔相等的间断时点数列。
在统计工作中，对现象每天的变动情况都进行登记是有困难的，为简化登记手续，往往每隔一定时间登记一次，如定期盘点的期末库存，十年一次人口普查等。若登记的间隔期相等，数值为时点指标，所记录的数据形成的就是间隔相等的间断时点数列。
为了解决时点数列不能相加的问题，对相邻两个数据可采用中点公式进行平均，平均后的数据代表每期（时间周期由每天变为每期）的数据：
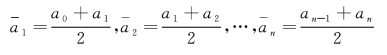
由于平均数具有代表性作用，它既可以代表长期水平，也可以代表短期水平，甚至某一时间点上的水平，这样就意味着每一期的数据都是已知的，且平均数是可以相加的，从而将间断时点数列过渡为连续性时点数列。
计算公式为：
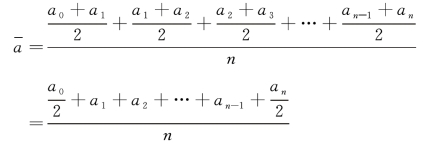
或
由于时点数列每期由期初水平和期末水平两个数据构成，时期数要比数据个数少一个，若数列从a0 开始，分母应为n；若数列从a1 开始，分母应为n -1。
从公式可以看出，经过简化，序时平均数的计算方法变为二分之首项，加中间各项，再加二分之末项，这种计算方法称为首尾折半法。
【例8-4】 某企业某年第二季度商品库存资料如表8-9 所示。要求：计算第二季度的平均库存量。
表8-9 商品库存资料
解 第二季度的各相邻两月平均库存量计算如图8-4 所示。
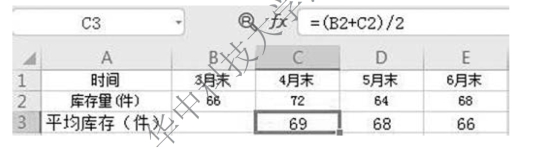
图8-4 第二季度的各相邻两月平均库存量计算
第二季度平均库存量计算如图8-5 所示。
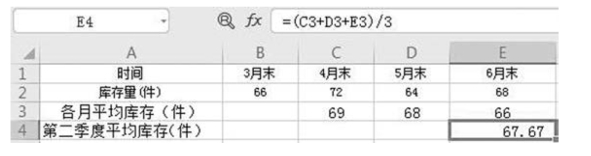
图8-5 第二季度平均库存量计算
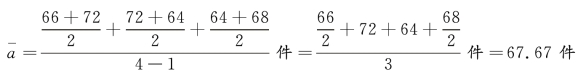
第二种，间隔不等的间断时点数列。
如果时点数列相邻时点间隔不等，就必须首尾折半后以时间间隔作为权数，采用加权平均法计算序时平均数。该加权平均法用于根据不定期抽查、不定期盘点数据编制的时间数列。
设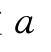
为序时平均数，f 为各时点间隔的长度，则计算公式为：
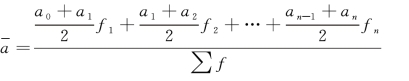
【例8-5】 某企业2018 年资产清查共进行4 次，所得资料如表8-10 所示。要求：计算该企业2018 年的平均资产金额。
表8-10 资产清查资料
解 由于清查相邻时点间隔长度不相等，宜采用加权平均法。四次资产清查时间间隔分别为5 个月、3 个月和4 个月，则该企业2018 年的平均资产金额为：
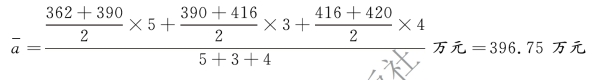
（二）根据相对数动态数列计算序时平均数
由于相对数属于派生指标，是由同期的两个相关绝对数对比而来的，相对数动态数列是由两个同时期相关总量指标时间数列在相应时间上指标数值对比的比率组成的。
不同时期的相对指标数值是不能加和的，因而相对数动态数列序时平均数不能直接由各期相对数简单平均计算，应正确区分分子数列、分母数列的性质，即它们是时期数列还是时点数列，间隔相等还是间隔不相等，然后根据数列的不同性质，分别计算分子数列、分母数列的序时平均数，再进行对比，求得相对数的序时平均数。
1.根据两个时期数列对比所形成的相对数动态数列计算序时平均数
当分子数列和分母数列都是时期数列时，数列中每个指标都是时期指标。
设a 表示分子数列的指标数值，b 表示分母数列的指标数值，c 表示所形成的相对数动态数列的指标数值，则有c=
再设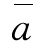
为分子数列的序时平均数
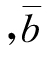为分母数列的序时平均数
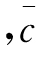为相对数动态数列的序时平均数，则相对数动态数列序时平均数的计算公式为：
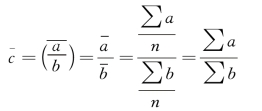
根据所掌握资料的不同，分为以下两种情况。
（1）分子数列和分母数列均已知，可直接利用公式计算。
【例8-6】 某企业第二季度各月生产计划完成情况如表8-11 所示。
表8-11 生产计划完成情况1
要求：计算第二季度平均计划完成程度。
解 第一步，分别计算分子数列、分母数列的序时平均数：
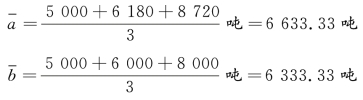
第二步，代入计划完成相对数动态数列序时平均数计算公式：
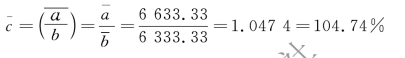
（2）所掌握的资料不齐全，无法直接计算，需要调整。要根据分子数列、分母数列与相对数动态数列之间的关系，推算出所需资料，分以下两种情况。
第一种，分母数列与相对数动态数列已知，分子数列未知，根据三者之间的关系，推算出分子数列后，再利用公式计算。这时，相对数动态数列的序时平均数计算变为以相对数动态数列为变量，以分母为权数计算加权平均数的形式。
【例8-7】 某企业第二季度各月生产计划完成情况如表8-12 所示。
表8-12 生产计划完成情况2
要求：计算第二季度平均计划完成程度。
解 要计算平均计划完成程度，但各月实际产量未知，属于资料不全，无法直接计算，但给出了计划产量数列和计划完成程度数列，各月实际产量数列可推算求出。
则4 月份实际产量为：5000吨×100%=5000 吨。5 月份实际产量为：6000吨×103%=6180吨。6 月份实际产量为：8000 吨×109%=8720 吨。
代入相对数动态数列序时平均数计算公式：
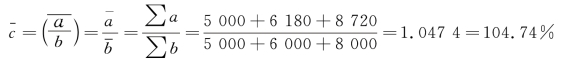
第二种，分子数列与相对数动态数列已知，分母数列未知，根据三者之间的关系，推算出分母数列，再利用公式计算。这时，相对数动态数列的序时平均数计算变为以相对数动态数列为变量，以分子为权数计算加权调和平均数的形式。
【例8-8】 某企业第二季度各月生产计划完成情况如表8-13 所示。
表8-13 生产计划完成情况3
要求：计算第二季度平均计划完成程度。
解 此处属于分母数列未知，同样可推算出分母数列。
则4 月份计划产量为：5000 吨÷100%=5000 吨。5 月份计划产量为：6180 吨÷103%=6000吨。6 月份计划产量为：8720 吨÷109%=8000 吨。
代入公式：
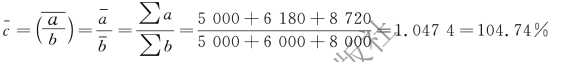
2.根据两个时点数列对比所形成的相对数动态数列计算序时平均数
如果相对数动态数列是由两个时点数列对比形成的，则计算序时平均数时要区分间隔是相等还是不相等，间隔相等时用简单平均数计算方法，间隔不相等时用加权平均数计算方法。
（1）分子数列、分母数列均为间隔相等的时点数列，序时平均数计算公式为：
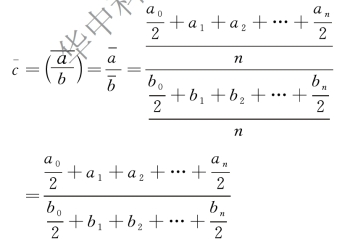
【例8-9】 某农场第二季度生产工人与全体职工人数统计资料如表8-14 所示。
表8-14 生产工人与全体职工人数统计资料1
要求：试计算第二季度生产工人与全体职工的平均比重。
解 生产工人人数、全体职工人数均为间隔相等的时点数列，则直接计算：
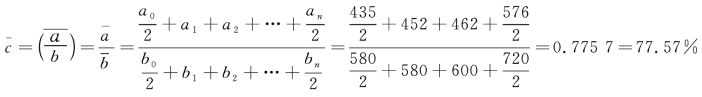
（2）分子数列、分母数列均为间隔不相等的时点数列，应以间隔时间长度为权数，采用加权平均法计算序时平均数。计算公式为：
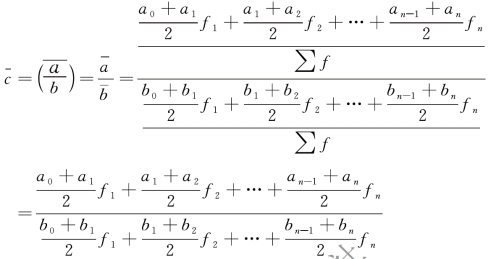
【例8-10】 某农场2018 年生产工人与全体职工人数统计资料如表8-15 所示。
表8-15 生产工人与全体职工人数统计资料2
要求：计算该农场生产工人人数占全体职工人数的平均比重。
解 由于以上时点数列相邻时点间隔不相等，宜采用加权平均法，计算序时平均数。表8-15 中的四次统计的时间间隔分别为5 个月、3 个月和4 个月，则该地区2018 年的月平均比重
为：
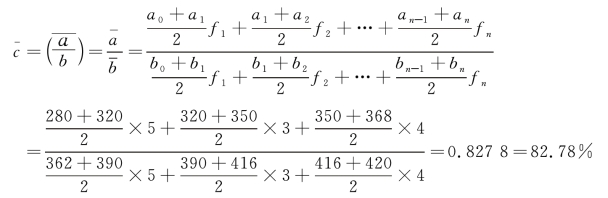
3.根据时期数列和时点数列对比所形成的相对数动态数列计算序时平均数
如果相对数动态数列中，分子是时期数列，分母是时点数列，则应分别计算分子数列和分母数列的序时平均数，然后再将它们对比求得相对数动态数列的序时平均数。在计算分母数列（时点数列）的序时平均数时，要区分间隔相等和间隔不相等两种情况。
第一种，当分母数列（时点数列）间隔相等时，分子数列用简单算术平均数作为序时平均数，分母数列用首尾折半法计算序时平均数。相对数动态数列的序时平均数计算公式为：
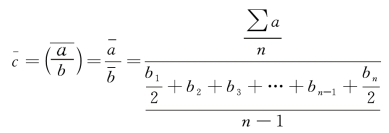
【例8-11】 某商城某种商品2018 年第二季度各月商品流转额与商品库存额资料如表8-16所示。
表8-16 第二季度各月商品流转额与商品库存额资料
要求：计算第二季度平均商品流转次数。
解 平均商品流转次数=平均商品流转额÷平均商品库存额。
第一步，计算商品流转额序时平均数。商品流转额是时期指标，用简单算术平均数作为序时平均数：
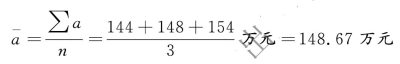
第二步，计算商品库存额序时平均数。商品库存额是间隔相等的时点指标，采用首尾折半法计算序时平均数：
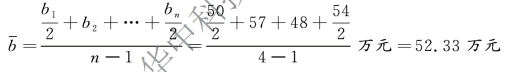
第三步，代入公式计算平均商品流转次数：
则第二季度平均商品流转次数为2.84 次。
第二种，当分母数列（时点数列）间隔不相等时，分子数列（时期数列）用简单算术平均数作为序数平均数，分母数列用加权算术平均数作为序数平均数。相对数动态数列的序时平均数计算公式为：
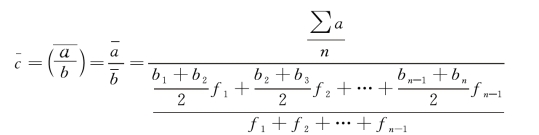
注意：以上两个计算公式中，分子数列（时期数列）比分母数列（时点数列）少一项。
（三）根据平均数动态数列计算序时平均数
根据平均数动态数列计算序时平均数的方法和原理与根据相对数动态数列计算序时平均数的方法和原理相同，即分别计算分子数列和分母数列的序时平均数，然后将两个序时平均数进行对比而求得。
设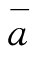
为分子数列的序时平均数
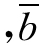为分母数列的序时平均数
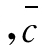为平均数动态数列的序时平均数，则计算公式为：
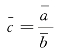
【例8-12】 某企业工人人数及月平均工资资料如表8-17 所示。
表8-17 工人人数及月平均工资资料
要求：计算该企业上半年工人的月平均工资。
解 月平均工资=平均工资×平均工人人数，计算过程如图8-6 所示。
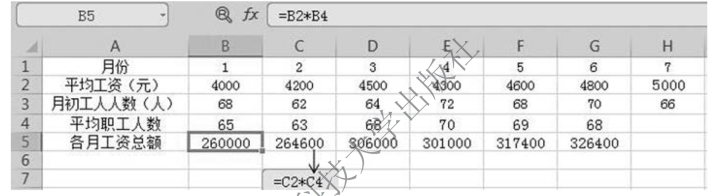
图8-6 月平均工资计算过程
月平均工资为：
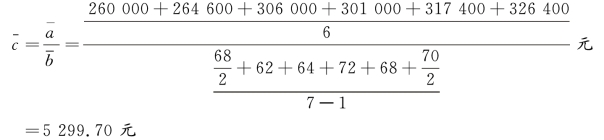
计算平均发展水平时应注意两个问题：
其一，平均发展水平的计算，只适用于那些在研究期间比较平稳（变化不大）或者短期上下波动较大但长期趋势不明显的现象。如果现象在发展变化过程中，有明显的向上或者向下的趋势，则需要进行趋势分析，此时计算平均发展水平没有实际意义。例如，将一个人的身高按出生到成年各时期进行平均，所得数值既不能代表过去身高，也不能代表现在身高，更不能代表未来身高。
其二，对间隔相等和间隔不相等的间断时点数列，在计算序时平均数时都假定两个相邻时点之间的数量变动是均匀的，因此，用这两种方法计算得到的序时平均数只是一个近似值。时点数列的时间间隔越长，这种假定性越大，其准确性也就越差。