三、相关系数
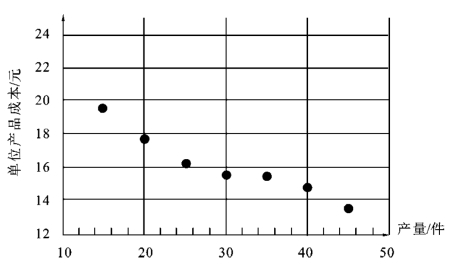
图7-3 产量与单位产品成本单变量相关图
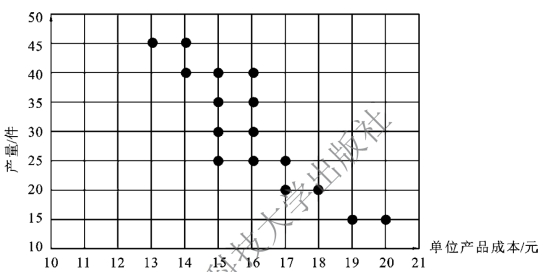
图7-4 产量与单位产品成本双变量相关图
无论是相关表还是相关图,尽管可以反映两个变量之间的相关关系及其相关方向,但无法确切地表明两个变量之间相关关系的密切程度。要判断变量之间相关关系的密切程度,需要借助定量分析指标。
相关系数是在线性相关的条件下,用以反映两变量间线性相关密切程度的统计指标,其基本算法是英国统计学家皮尔逊所创的乘积动差法,简称积差法。相关系数用r 表示,基本公式为:
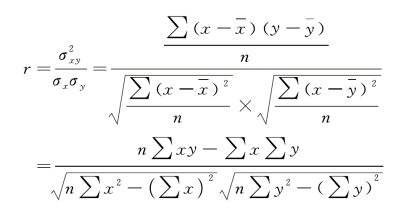
(一)相关系数的性质
相关系数的值介于-1 与+ 1 之间,即-1 ≤r ≤+ 1。
(1)r >0 为正相关;r <0 为负相关。
(2)| r |=0 表示不存在线性关系。
(3)| r |=1 表示完全线性相关。
(4)0 <|r|<1 表示存在一定程度的线性相关,且|r|越接近1,两变量间线性相关关系越密切;| r |越接近0,表示两变量的线性相关关系越弱。
①| r |<0.4 为低度线性相关。
②0.4 ≤| r |<0.7 为显著性线性相关。
③0.7 ≤| r |<1 为高度显著性线性相关。
【例7-4】 以表7-2为条件,计算这30个同类型企业的产量(x)与单位产品成本(y)的相关系数。
解 计算过程如表7-5 所示。
将n=7,Σx,Σy,Σxy,Σx2,Σy2 代入相关系数公式:
表7-5 相关系数计算过程
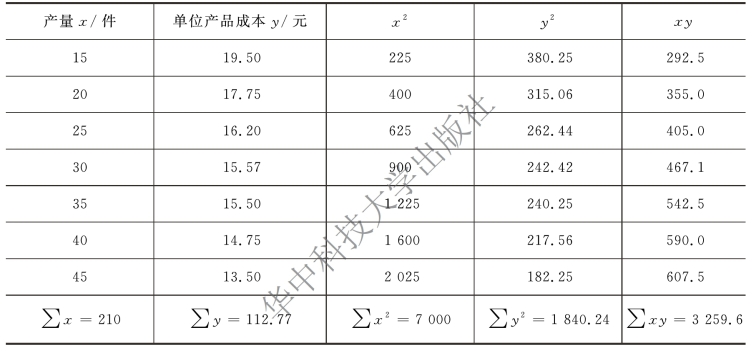
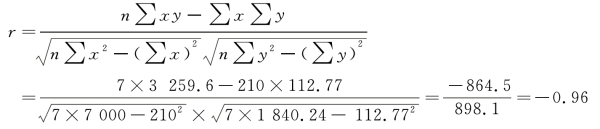
根据计算结果,产量与单位产品成本高度显著性线性相关,产量的变化能够解释单位成本变化的96%。
(二)使用相关系数时应注意的问题
(1)相关关系不是因果关系。
相关系数只度量变量间的线性关系,它并不能说明两变量间是否有因果关系。因果关系是指某个因素的存在一定会导致某个特定结果的产生。“伴随”和“导致”是有区别的。例如,夏天的海边,太阳镜和雪糕的销售量存在相关性,但不是因为太阳镜卖得多所以雪糕就卖得多,而是因为它们受同一日光辐射强度的影响,得到了共同的结果。因果关系一定是相关关系,相关关系不一定是因果关系。
(2)注意虚假相关。
计算相关系数的前提是,变量存在相关关系,相关系数只是相关关系的一种测算。任何两种(组)数字都可以计算出一个相关系数,但有没有相关关系还需要结合专业理论知识来进行判断。例如,有人曾对教师薪金的提高和酒价的上涨做了相关分析,计算得到一个较大的相关系数,这是否表明教师薪金提高会导致酒价上涨呢?经分析,事实是经济繁荣导致教师薪金和酒价同时上涨,而教师薪金提高和酒价上涨之间并没有直接关系。
(3)注意相关关系成立的数据范围。
