重复随机抽样及其样本分布
重复随机抽样又称重置抽样或有放回抽样，它是指在抽取样本时，从总体中随机抽取一个单位，把结果记录下来，然后放回参加下一次抽取，每次抽取是在完全相同的条件下进行的，n次抽样就是n 次相互独立的实验；在整个抽选样本过程中，同一个单位可能多次被抽中。重复随机抽样条件下总体中的每个单位被抽取的机会完全相等。从N 个单位中随机抽取n 个单位组成样本有Nn 种抽法。
对按重复随机抽样的方法抽出的全部可能样本计算抽样指标与相应的概率，就可得到重复随机抽样的概率分布。
重复随机抽样根据总体性质分为变量总体抽样和属性总体抽样。
（一）变量总体抽样及其样本分布
在重复随机抽样条件下，变量的样本分布，是样本的概率分布，反映样本分布的状况及抽样指标接近总体参数的程度。
例如，假设全及总体为4 名工人，分别是A、B、C、D，日产量分别为60 件、70 件、80 件、90 件，在重复抽样条件下，要随机抽选出2 名工人作为样本，以此来观察所有可能样本与全及总体之间的关系（这里全及总体只有4 个单位，样本只有2 个单位，主要是为了简化计算过程）。
1.所有可能样本的构成
已知N=4，n=2，所有可能的样本数目为Nn=42=16，排列如图6-1 所示。
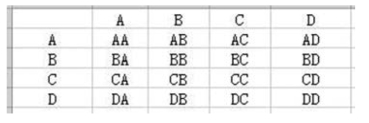
图6-1 所有可能的样本排列
2.所有可能样本的分布与全及总体单位分布的关系
所有可能样本的分布指所有可能样本的平均数与之对应的概率。样本平均数用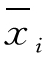
表示，其计算如图6-2 所示。
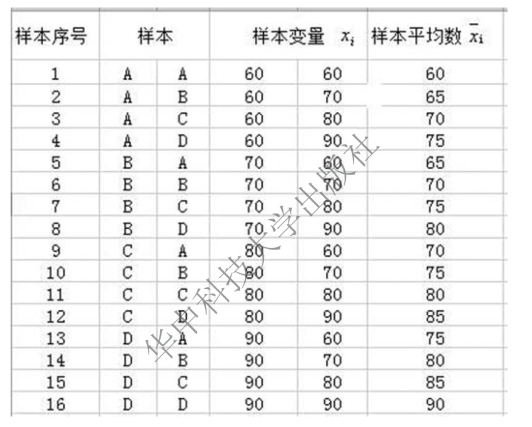
图6-2 所有可能样本的样本平均数计算
将这16 个样本的样本平均数进行排序，编制分布数列并分别计算概率，如图6-3 所示。
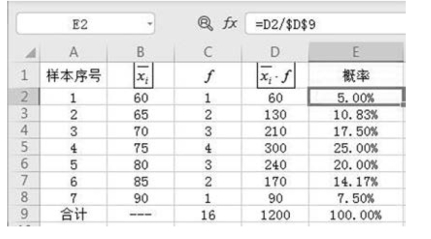
图6-3 对样本平均数进行排序并编制分布数列
绘制概率散点图，如图6-4 所示。
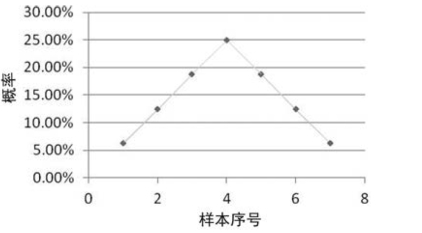
图6-4 概率散点图
由此可以看出，所有可能样本分布呈现正态分布，其单位分布与全及总体一致，具有代表性。
3.数学期望值与全及总体平均数的关系（无偏性）
样本平均数的平均数叫数学期望值，用E（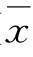
）表示。
设样本容量为n，所有可能样本的样本平均数为
，有如下计算方法。
（1）对于未分组资料：
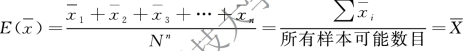
（2）对于分组资料：
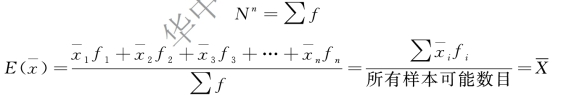
以上案例中，E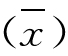
计算如下：
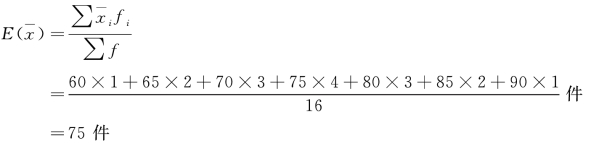
总体平均数：
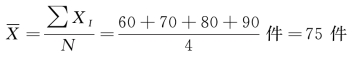
由此可见，在重复随机抽样中，所有可能样本的样本平均数的平均数与全及总体的总体平均数相等，满足无偏性。
在实际统计工作中，由于全及总体平均数是未知的，需要用样本平均数来推断，只要坚持随机原则，无论抽中哪一个样本，都不会产生系统性误差。
4.抽样平均误差与全及总体方差的关系
在以上案例中，可以抽出16 个可能样本，因而样本数值就有16 个，这16 个数值有大有小，要反映抽样误差的一般水平，就有必要计算抽样平均方差。
（1）抽样平均方差。
抽样平均方差是指每一个可能样本的抽样指标值与总体指标值之间的方差，即一系列抽样指标与全及指标的方差。一般用
表示。
在以上案例中，样本容量为n=2，总体单位数N=4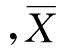
=75 件。所有可能样本方差计算如图6-5 所示，总体方差计算如图6-6 所示。
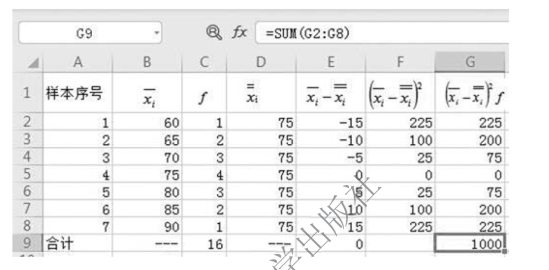
图6-5 所有可能样本方差计算
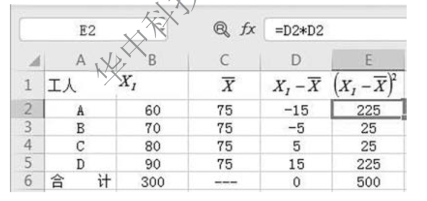
图6-6 总体方差计算
总体方差计算：
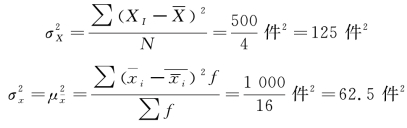
将所有可能样本方差与总体方差进行比较：
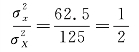
为了便于比较，将分子化为相同的数值：
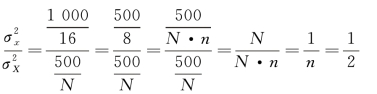
由此可知，在以上案例中，所有可能样本方差比总体方差要小，而且所有可能样本的方差还是总体方差的样本容量分之一。根据这一情况，需要研究具有普遍意义的所有可能样本平均数的方差与总体方差的关系。
实际工作中，由于全及总体是未知的，不可能把所有的可能样本的样本统计量全都计算出来，要根据所有可能样本方差与总体方差之间的数量关系，来确定所抽样本的方差。
设所有可能样本变量为x1，x2，…，xn，在重复抽样的情况下，x1，x2，…，xn 是相互独立的，推导过程如下：
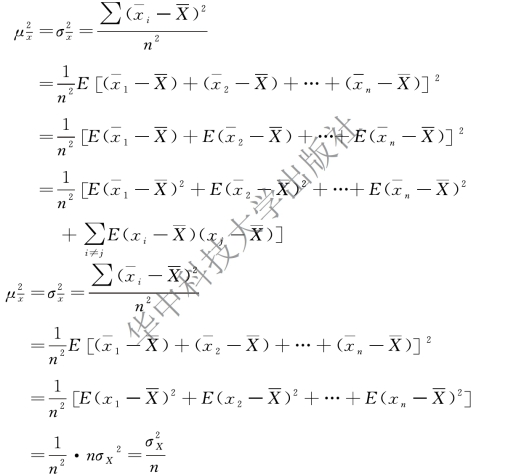
从方差公式的推导结果可以看出，抽样平均方差与全及总体方差的关系可以表示为：
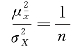
即
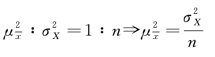
这说明抽样平均数的平均方差要比总体方差小得多，抽取一个样本计算得出的样本方差与全及总体方差的差异可能很大，但抽取若干个单位加以平均之后，抽样平均数的方差相对全及总体方差大为减小。
（2）抽样平均误差与全及总体方差的关系。
抽样平均误差指每一个可能样本的指标值与总体指标值之间的平均离差，即一系列样本指标的标准差，根据抽样平均方差与全及总体方差的关系式，在等号两边分别开平方求得，一般用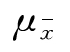
表示：
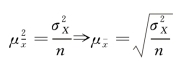
以下从一致性角度来判断抽样推断的样本统计量是否合乎要求。
前文案例中所有样本的平均误差：
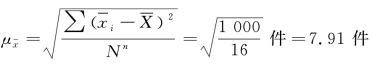
可以利用全及总体公式来验证：
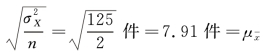
从以上推导可以看出：
①抽样平均误差与全及总体方差成正比。全及总体各单位之间差异越大，抽样平均误差越大；反之，全及总体各单位之间差异程度越小，抽样平均误差就越小。可以设想，若全及总体各单位之间无差异，无论随机抽取哪一个样本，其样本指标和总体指标都是一样的，则抽样（平均）误差为0。
②抽样平均误差与样本容量的平方根成反比。其他条件不变时，样本容量越大，样本对总体的代表性越高，抽样平均误差越小。随着样本单位数n 的增大，样本统计量将在概率意义上越来越接近总体真实值，符合一致性要求。
③计算抽样平均误差时，除样本容量外，还需要知道全及总体方差。全及总体方差可用过去同类问题全面调查或抽样调查的经验数据代替；如果无可代替，一般用样本总体的相应指标来代替。
在实际工作中，一般抽样只抽一个样本或者几个样本，被抽中的这一个或几个样本与总体之间的误差就用抽样平均误差来代表，也称平均抽样误差。
【例6-1】 从某厂生产的10000 只日光灯管中随机抽取100 只进行检查，假如该类灯管平均使用寿命的标准差为100 h，试计算该厂日光灯管平均使用寿命的平均抽样误差。若要将平均抽样误差降为原来的1/3，样本容量将为多少？
解 在重复随机抽样条件下进行计算。
①平均抽样误差：
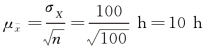
②新的样本容量：
已知
，则
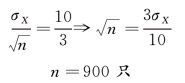
若要将平均抽样误差降为原来的1/3，样本容量将为900 只。
（二）属性总体抽样及其样本分布
在重复随机抽样条件下，对于属性总体，成数的样本分布是样本成数的概率分布，反映成数分布的形状及样本统计量接近总体参数的程度。
1.样本成数的抽样分布
设p 为样本成数，P 为总体成数，由于成数的平均数就是成数本身，样本成数的抽样分布数学期望值为：E（p）= P。
2.成数的方差与标准差分布
在掌握抽样平均数的平均误差的基础上，计算成数的方差和标准差时只需将变量换为成数即可。
（1）成数的方差。
所有可能样本的成数方差与总体方差的关系：
即
可用文字表述为：
（2）成数标准差。
成数标准差，又称为成数平均抽样误差，用于反映样本成数与总体成数的平均误差程度，它是衡量用p 估计P 时所可能产生的误差大小的指标，用μp 表示：
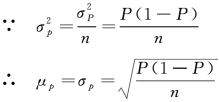
从上式可以看出，成数平均抽样误差也是受总体方差和样本容量影响的。
不论是抽样平均数的抽样平均误差计算，还是抽样成数的抽样平均误差计算，所用的标准差都是全及总体的标准差，但实际上，无论是在抽样之前，还是在抽样之后，全及总体的标准差都是未知的，所以，一般用样本总体的相应指标来代替全及总体的标准差，也可取最大值0.5。
【例6-2】 从某厂生产的10000 件产品中，随机抽取1000 件进行调查，测得有85 件不合格。试求产品合格率的抽样平均误差。
产品合格率的抽样平均误差为0.88%。