等级相关及等级相关系数
等级相关是用非参数方法了解两个事物之间关系的一种方法，适用于两列顺序变量之间的相关方向和密切程度的测定。由于社会经济现象具有复杂性，有许多现象难以以精确数字形成统计数列，而只能根据主观判断，评定等级，排列顺序。
常用的等级相关系数有斯皮尔曼等级相关系数、肯德尔一致性相关系数等。
（一）斯皮尔曼等级相关系数
两变量是等级测量数据，且总体不一定呈现正态分布，样本容量也不一定大于30，这样的两个变量相关，称为等级相关（斯皮尔曼等级相关）。
斯皮尔曼等级相关系数（rs）与相关系数一样，取值在-1 到+ 1 之间，rs ＞0 表示正相关，rs ＜0 表示负相关，rs=0 为不相关，区别是斯皮尔曼等级相关系数是在等级的基础上计算的，较适用于反映序列变量的相关。计算公式为：
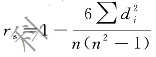
式中：rs 为斯皮尔曼等级相关系数，di 为两变量每一对样本的等级之差，n 为样本容量。
斯皮尔曼等级相关系数的计算步骤：计算两变量等级之差di→计算
→计算
→代入公式计算rs。
【例7-5】 某项比赛共有10 名选手参加，甲、乙两组评委评定的名次如表7-6 所示。
表7-6 甲、乙两组评委评定的选手名次
要求：通过计算判断两组评委所评定名次的相关性。
解 等级相关系数计算过程如表7-7所示。
=24，n=10，代入公式计算：
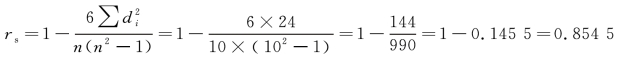
0.7 ≤|rs|＜1，为高度显著性线性相关。
表7-7 等级相关系数计算过程
若已知两组变量值，但不知道等级顺序，可先换算成等级，再利用公式计算等级相关系数。
【例7-6】 某项比赛有12 名选手参加，由评委组和观众组分别评分。评委组和观众组评分如表7-8 所示。
表7-8 评委组和观众组评分
要求：判断两组的意见是否一致。
解 首先对评委组和观众组各自的评分进行排序，确定等级，计算等级差，再利用公式计算等级相关系数。计算过程如表7-9 所示。
表7-9 评委组和观众组评分等级相关系数计算过程
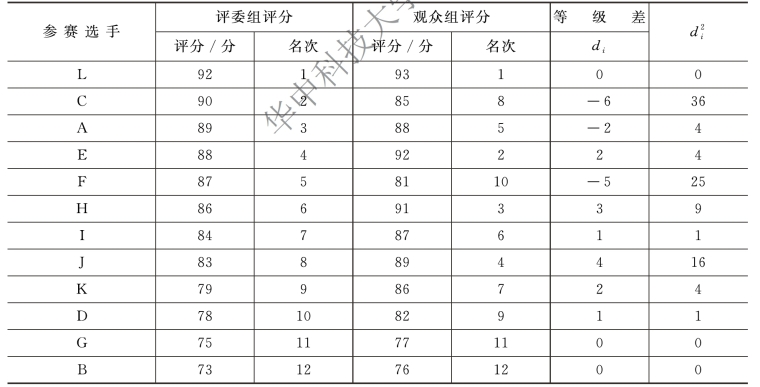
=100，n=12，代入公式计算：
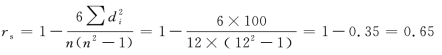
0.4 ≤| rs |＜0.7，为显著性线性相关，评委组和观众组的意见一致程度为65%。
（二）肯德尔一致性相关系数
当多个变量以等级顺序表示时，这几个变量之间的一致性程度，称为肯德尔一致性相关系数。适用肯德尔一致性相关系数的数据资料一般是采用等级评定的方法收集的，是客观数据，用以测试、验证人的水平、判断力。计算公式为：
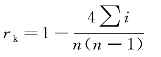
式中：Σi代表偏差次数之和，n代表变量值个数。
计算肯德尔一致性相关系数时，偏差次数可采用连线的方法确定，一个交叉点代表出现一次偏差。等级偏差越大（多），意味着错误越大。
【例7-7】 在一次水平能力测试中，某产品共有十个等级，分两组，第一组依次为1、2、3、4、5 五个等级，第二组依次为6、7、8、9、10 五个等级，应试者李某对第一组产品等级的判断依次为5、2、1、4、3，对第二组的判断依次为9、8、10、7、6。用肯德尔一致性相关系数评价李某的水平。
解 用连线的方法确定偏差数量，如图7-5 所示。
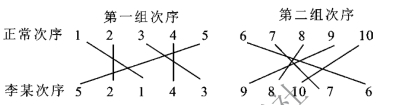
图7-5 确定偏差数量
共有14 个交叉点，李某的判断共出现14 次偏差，代入公式计算：
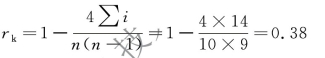
| r |＜0.4，为低度线性相关，表明李某的判断力较低。