抛物线趋势分析与预测
抛物线又称二次曲线，是指现象随时间的推移不是直线上升或直线下降，而是出现先升后降，或先降后升的趋势，其时间数列的折线图上有明显的拐点，则该时间数列为抛物线型。一般来讲，一个弯为二次曲线，两个拐弯为三次曲线，依次类推。抛物线趋势的数学特征是：时间数列中的二级增长量（即逐期增长量的逐期增长量）大体相同。
二次曲线趋势方程：
抛物线有三个待定参数，分别是a、b 和c，需要建立三个标准方程，联立成方程组。抛物线趋势分析与预测可采用两种方法：一种是最小平方法（及简捷法）；另一种是三点法。
（一）最小平方法
利用最小平方法对抛物线拟合趋势方程的原理和对直线基本相同。所不同的是，抛物线有三个待定参数，要建三个方程，且要求趋势值与实际观察值的离差平方和具有最小值，即
设抛物线趋势方程为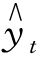
=a+bt+ct2，将
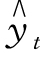=a+bt+ct2代入Σ（yt -
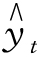）2，得
此式仍为二次曲线，具有最小值；a，b，c 为待定参数。推导如下。
设Q= Σ（yt-a-bt-ct2）2，分别对a，b，c求导数。令Q'=（Σ（yt-a-bt-ct2）2）'=0，求导过程如下：
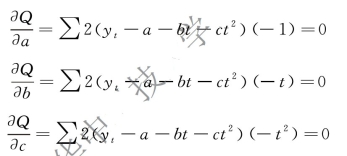
联立成方程组：
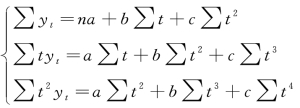
这样，组成一个三元一次方程组，将资料代入，解出a、b 和c，再代入抛物线方程，趋势方程就形成了。
【例9-8】 某产品某年1—9 月销售量统计资料如表9-1 所示。
表9-1 某产品1—9 月销售量统计资料 （单位：万吨）
要求：利用最小平方法建立预测模型并预测10 月份销售量。
解 从表9-1 中看出，随时间变化，销售量由低到高再到低，有一个明显的拐点，判断为呈抛物线趋势。
设抛物线方程为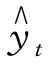
=a+bt+ct2，则方程组为：
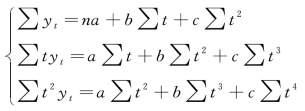
根据方程组要求计算的内容列表，计算过程如图9-21 所示。
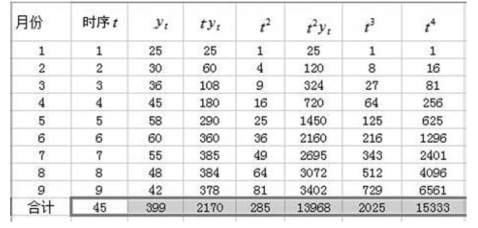
图9-21 最小平方法参数计算过程（抛物线趋势）
已知n=9，将图9-21 中的计算结果代入方程组：
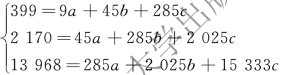
解方程得a=4.93，b=16.46，c= -1.35，则抛物线方程为：
检验过程如图9-22所示。通过计算，Σ（yt -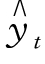
）=0，且绘制理论值与实际值比较图（见图9-23）发现，理论值与实际值变动趋势基本吻合，则方程有效，可以用来预测。
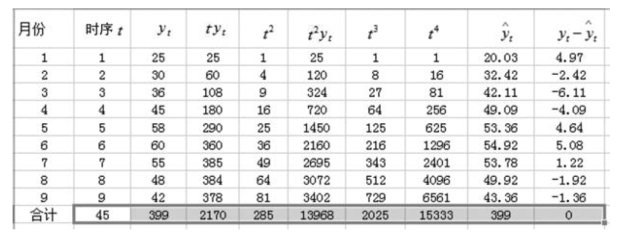
图9-22 检验抛物线方程（最小平方法）
10 月份销售量排在第10 期，t=10，代入方程：
即可预测10 月份销售量为34.10 万吨。
（二）简捷法
解最小平方法中的方程组时，数据比较大，项数比较多，可以进一步进行简化。当数列项数n 为奇数时，令t=…，-3，-2，-1，0，1，2，3，…；当数列项数n 为偶数时，令t=…，-5，-3，-1，1，3，5，…。由此可使Σt=0，Σt3=0，原方程组可简化为：
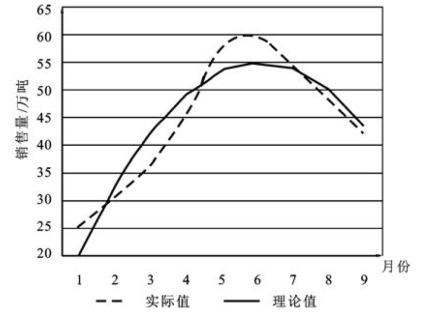
图9-23 理论值与实际值比较图
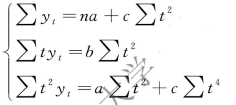
【例9-9】 已知资料如表9-1 所示。要求：采用简捷法建立预测模型并预测10 月份销售量。
解 按简捷法要求排序并计算。
设抛物线方程为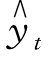
=a+bt+ct2，方程组为：
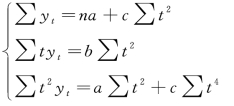
计算过程如图9-24 所示。
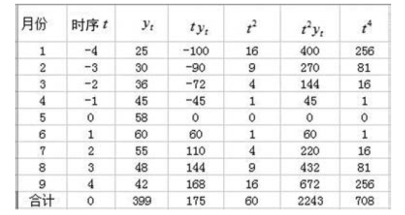
图9-24 简捷法参数计算过程
将n=9，Σyt=399，Σt2=60，Σtyt=175，Σt2yt=2243，Σt4=708代入抛物线方程组：
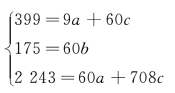
解方程组得a=53.36，b=2.92，c= -1.35，代入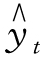
=a+bt+ct2 得
检验过程如图9-25所示。Σ（yt-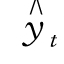
）=0，且理论值与实际值变动趋势基本吻合，方程有效，可以用来预测。
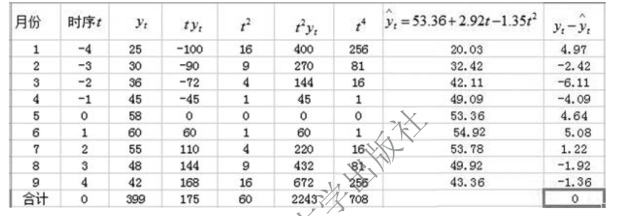
图9-25 检验抛物线方程（简捷法）
10 月份销售量排在第5 期，t=5，代入方程：
即可预测10 月份销售量为34.10 万吨。
（三）三点法
用三点法来估计抛物线方程预测模型的基本思路是，在抛物线上选取具有代表性的三个点来求预测模型的三个待定参数。
这三点的选择方法是：将时间数列平均分为三部分，分别进行加权，计算平均数，代入抛物线方程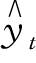
=a+bt+ct2，求出a，b，c。具体步骤如下。
第一步：确定项数。时间数列总项数必须是3 的倍数，如果不是，舍弃最初部分，然后重新排序。
第二步：分组。将原时间数列平均分为相等的三部分，即第一部分为y1，y2，…，yi，第二部分为yi+1，yi+2，…，yk，第三部分为yk+1，yk+2，…，yn。
第三步：对每一部分的时序（t）与观察值（yt）分别计算加权平均数，权数z 应由前到后分别取
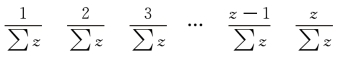
设A、B、C 分别代表三点，坐标分别为
，则计算过程如下。
A 点坐标
：
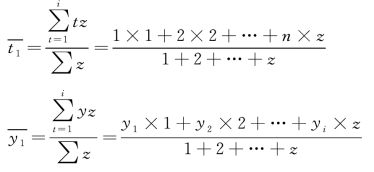
B 点坐标
：
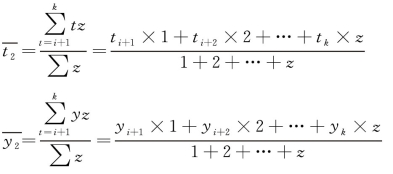
C 点坐标
：
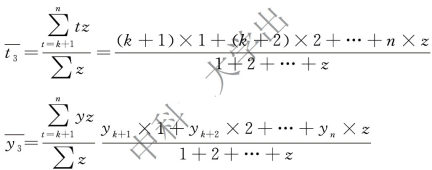
将A、B、C 三点的坐标值代入抛物线方程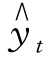
=a+bt+ct2，联立方程组：
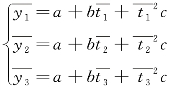
求出a，b，c；再将a，b，c的值代入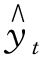
=a+bt+ct2，建立趋势方程，利用这个方程就可以进行预测了。
【例9-10】 某食品销售量受季节变动影响较大，1—9 月销售量资料如表9-2 所示。
表9-2 某食品1—9 月销售量资料 （单位：吨）
要求：利用三点法判断趋势并预测10 月份的销售量。
解 绘制销售量变动示意图，如图9-26 所示。
从图9-26 可以看出，销售量从1 月到7 月是下降的，从7 月到9 月是上升的，由降到升有明显的拐点，初步判断为抛物线趋势。
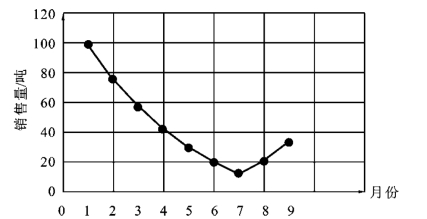
图9-26 销售量变动示意图
设：抛物线方程为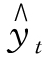
=a+bt+ct2。
总项数为9，是3 的倍数，将原数列均分为三部分，重新排序，计算过程如图9-27 所示。
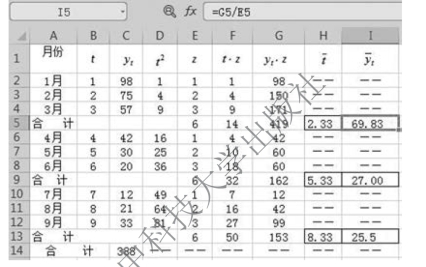
图9-27 三点法参数计算过程（3 项）
A、B、C 三点的加权平均数为：
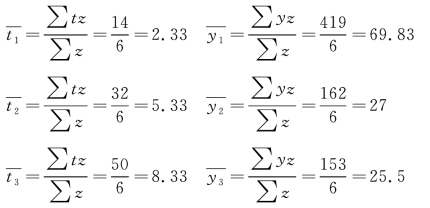
代入抛物线方程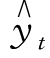
=a+bt+ct2，联立方程组：
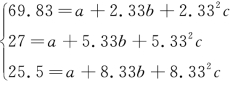
解方程得a= 131.72，b= -31.88，c= 2.30，代入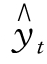
= a+bt+ct2 得
检验过程如图9-28 所示。将各期理论值与实际值绘图进行比较，如图9-29 所示，可以看出，两者基本一致（毕竟两者受的影响因素不同，实际观察值除受长期因素影响以外，还受其他因素影响）。由此可知，方程有效，可以用来预测。
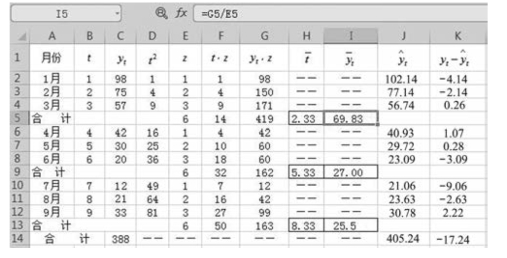
图9-28 检验抛物线方程（三点法，3 项）
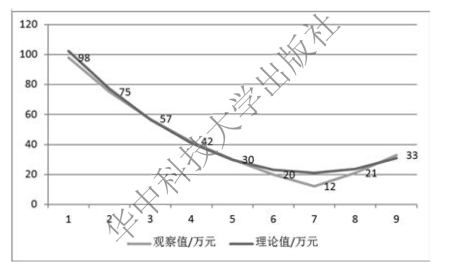
图9-29 实际观察值与理论值比较图
10 月份销售量排在第10 期，则t=10，代入方程：
即可预测第10 期销售量为42.53 吨。
采用三点法，每部分为三项或五项的居多，也最为常用，为了简化方程组求解过程，将每部分取三项或五项数据的作为特例，表达式也有所不同。只要计算出
，不用解方程组，直接能够推出a，b，c 的值。推导过程如下。
1.每部分取三项数据时
可变形得
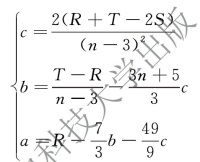
【例9-11】 以图9-27 所示数据为例进行计算。
已知R= 69.83，S= 27，T= 25.5，则
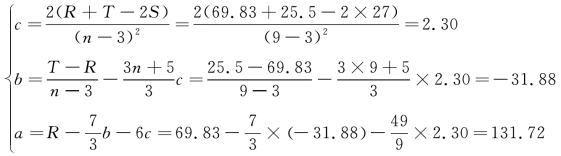
代入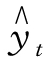
=a+bt+ct2：
与此前结果一致。
2.每部分取五项数据时
设
，分别代表首、中、尾三段的加权平均数，n=15，z 为权数（z=1，2，3，4，5，Σz=15），则三点坐标
为：
【例9-12】 某地区2001—2015 某农产品销售量统计资料如图9-30 所示。
要求：判断趋势，利用三点法拟合趋势方程并预测2016 年销售量。
解 绘制销售量变动图，如图9-31 所示。
设抛物线方程为：
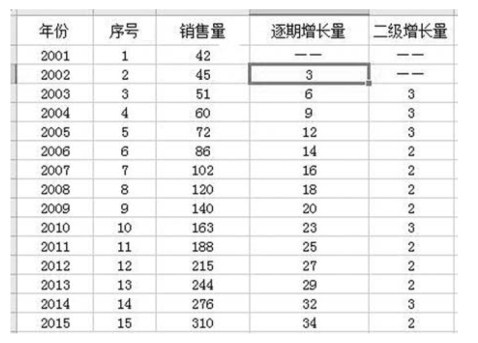
图9-30 某农产品销售量统计资料（单位：万吨）
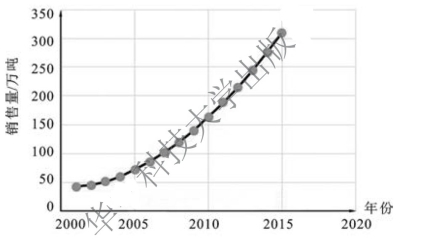
图9-31 销售量变动图
参数计算过程如图9-32 所示。
n= 15，三点的加权平均数为：
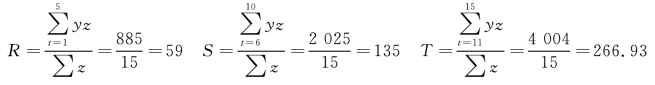
将以上已知数值代入方程组：
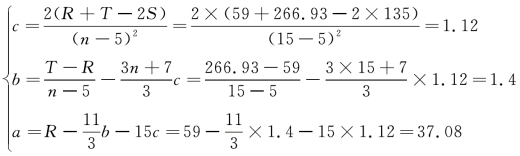
代入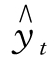
=a+bt+ct2 得
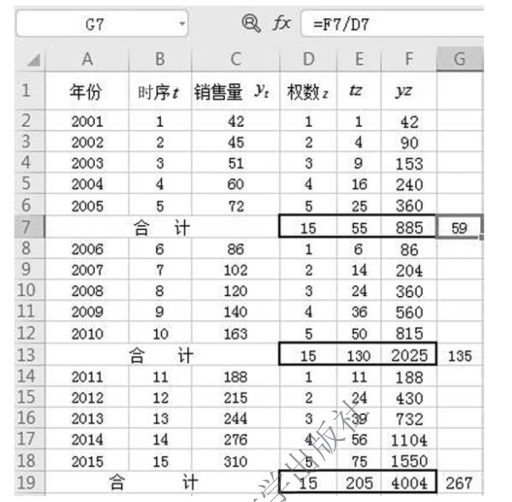
图9-32 三点法参数计算过程（5 项）
检验过程如图9-33 所示。
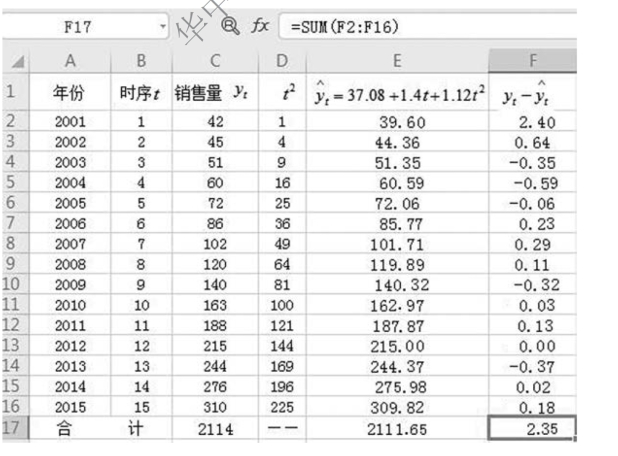
图9-33 检验趋势方程（三点法，5 项）
从图9-33 中可以看出，偏差极小，趋势方程有效，可以用来预测。
2016 年销售量排在第16 期，即t=16，代入方程计算：
2016 年销售量预测为345.90 万吨。