三、几何平均数
几何平均数通常用来计算平均比率和平均速度。当所掌握的变量值本身是比率的形式,且各比率的乘积等于总的比率时,就应采用几何平均数计算平均比率。几何平均数分为简单几何平均数和加权几何平均数,用G 表示。
(一)简单几何平均数
简单几何平均数适用于根据未分组资料来计算平均比率和平均速度的情况。
设n 个变量分别为x1,x2,x3,…,xn,则几何平均数的计算公式为:
![]()
式中:G 为几何平均数,n 为变量值的个数。
【例5-7】 某产品生产加工需要经过五道工序,各工序产品合格率分别为60%、70%、80%、85%、90%,计算平均合格率。
解 总的合格率等于各工序合格率的连乘积,符合几何平均数的适用条件,故需采用几何平均数计算方法。计算过程如图5-9 所示。
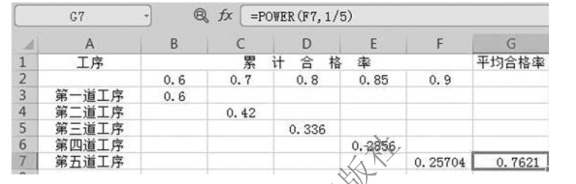
图5-9 平均合格率计算过程
列式计算平均合格率为:
![]()
(二)加权几何平均数
加权几何平均数适用于总体资料经过分组整理形成变量数列的情况。计算公式为:
![]()
式中:G 为几何平均数;fi 为第i 组的次数;i 为组数;n 为变量值的个数;xi 为第i 组的标志值或组中值。
【例5-8】 某人向金融机构贷款15 年,随利息调整,15 年来有2 年年利率为3%,3 年为5%,4 年为8%,4 年为10%,2 年为15%。求平均年利率。
解 利率的本质就是增长率,在计算时,可将利率“+ 1”转换为发展速度,该例转换为求平均发展速度,得到平均发展速度之后,再“-1”,即得平均年利率。计算过程如图5-10 所示。
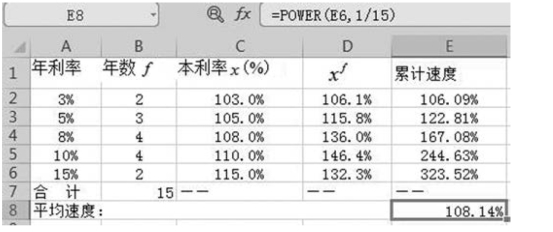
图5-10 平均年利率计算过程
列式计算平均发展速度:
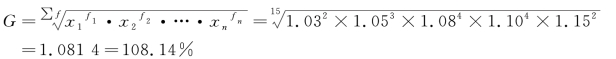
平均年利率为:
![]()
几何平均数的计算属于动态数列中平均增长量(率)的计算。
综上所述,算术平均数是应用最为广泛的一种平均数,因为其计算方法是与许多社会经济现象的数量关系相符合的,即许多社会经济现象总体各单位的标志值之和等于总体的标志总量,而且这种方法易于理解并具有优良的数学性质。调和平均数在实际应用中通常是作为算术平均数的变形使用的,即利用调和平均数的形式来计算算术平均数。数值平均数有一个最大的缺点——数据必须是已经发生的已知数据,对于正在发生的、数据不全的,就无法计算数值平均数,如当前某种农产品市场价格,可以采用另一种平均数即位置平均数来确定。
