一、移动平均法
移动平均法是一种简单平滑预测方法,根据时间数列逐项移动,依次计算包含一定项数的平均数,并据此对预测对象进行预测。其实质上是利用预测期之前各期观察值的加权平均数,对不同时期的数据给予不同的权重,分析出预测值。
移动平均法能有效地消除预测趋势中的随机波动,分为简单移动平均法与加权移动平均法。
(一)简单移动平均法
简单移动平均法是以原有时间数列为基础,按照一定项数计算简单移动平均数,以距离预测期最近的移动平均数作为预测期的预测值。
设n 为移动平均的项数,t 为时序,时间数列为:
![]()
则预测值为:
![]()
移动平均的项数根据原有数列本身的规律进行判断。
【例9-14】 某企业农产品2006—2018 年销售量统计资料如图9-39 所示。
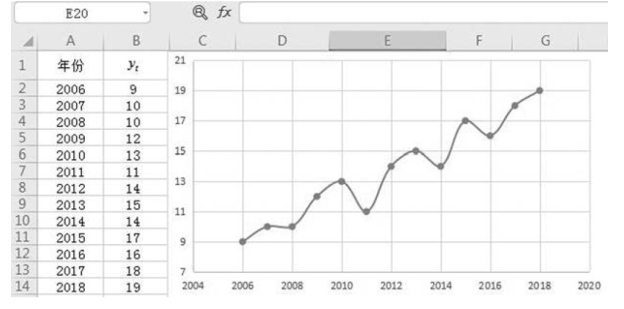
图9-39 2006—2018 年销售量统计资料(单位:吨)
要求:按三项移动平均,用简单移动平均法,预测2019 年销售量。
解 计算过程如图9-40 所示。各期理论值计算方法:
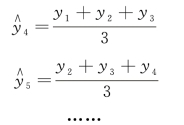
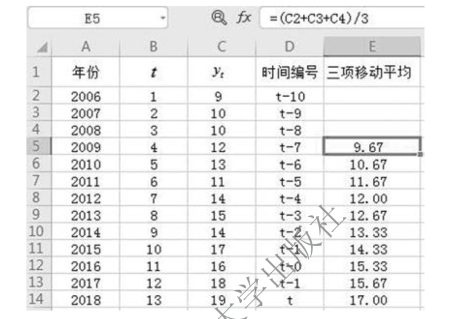
图9-40 简单移动平均法计算过程(3 项)
按三项简单移动平均计算,2019 年销售量预测值为:
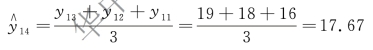
即可预测2019 年销售量为17.67 吨。
简单移动平均法将距离预测期远近不同的数值同等看待,认为每一期数据对预测期是一样重要的,采用此方法预测的数据有一定的滞后性。
(二)加权移动平均法
加权移动平均法认为,各期数值对未来判断的影响是不同的,距离预测期越近,影响越大,应给予较大的权重;反之,影响越小,给予的权重要小一些,也就是新数据给较大的权重,旧数据给较小的权重,这样克服了简单移动平均法对各期数据相同对待的缺陷。
设权数为z(z=n,n -1,…,2,1),则预测期为:
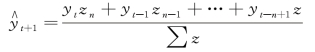
【例9-15】 已知资料如图9-39 所示,采用加权移动平均法,按三项移动平均计算并预测2019 年的销售量。
解 按三项移动平均,权数z 分别取3、2、1,各期理论值计算方法:
![]()
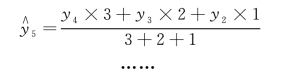
计算过程如图9-41 所示。
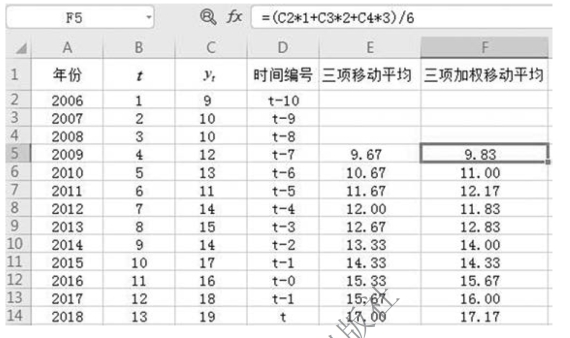
图9-41 加权移动平均法计算过程(3 项)
2019 年销售量预计为:
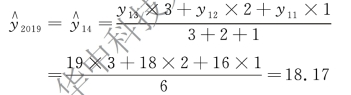
即可预测2019 年销售量为18.17 吨。
由此可见,在增长趋势下,采用加权移动平均法比简单移动平均法预测的数值要大。
