二、中位数
（一）中位数的概念
中位数和众数一样，也是一种位置平均数，主要用于测度顺序及数值型数据的集中趋势，所以又称为次序统计量。中位数是将总体各单位标志值按大小顺序排列后，处于中间位置的那个数值，用Me 表示。
从中位数的概念可见，在总体中，可大致理解为，小于中位数的数据占数据个数的一半，大于中位数的数据也占数据个数的一半，即中位数是将数据按大小顺序排列后，位于中间点的那个数据值。用中位数代表总体中所有指标值的一半水平，可以避免极端值的影响，在某些情况下更具有代表性，因为各变量值与中位数的离差绝对值之和最小。
（二）中位数的计算
根据所掌握的数据是否分组，中位数的计算分以下两种情况。
1.对于未分组的原始资料
（1）当数据量n 为奇数时，中位数计算公式为：
【例5-11】 某小组有9 名学生，身高资料如图5-17 所示。要求：计算身高的中位数。
图5-17 某小组学生身高资料
解 首先，进行排序，选择排序条件，以身高顺序确定中位数位次。共9 名学生，n= 9，则
确定中位数过程如图5-18 所示。
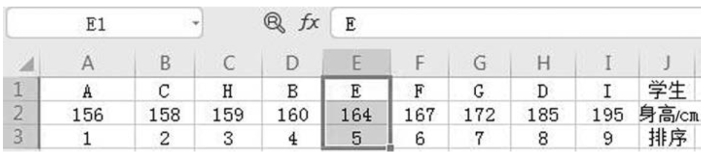
图5-18 中位数确定过程
然后，确定中位数：
（2）当n 为偶数时，中位数计算公式为：
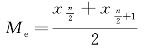
位次应为整数，由于
不是整数，取前后两个整数位次。
【例5-12】 某小组有10 名学生参加某项活动，身高资料如图5-19 所示。
图5-19 某小组10 名学生身高资料
解 排序并确定中位数位次，n=10，则取
前后两个整数位次，如图5-20 所示。中位数计算过程如下：
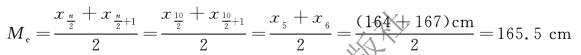
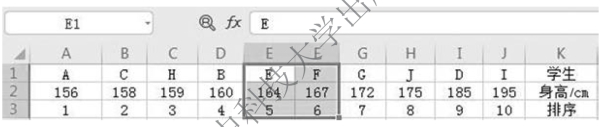
图5-20 中位数位次确定过程
2.对于分组资料
分组资料可分为单项式变量数列和组距式变量数列。
（1）根据单项式变量数列资料计算中位数时，由于变量值已经序列化，中位数可以直接按下面的方式确定。
①当Σf 为奇数时：
【例5-13】 某村有99 户人家，家庭人口分布资料如图5-21 所示。要求：计算中位数。
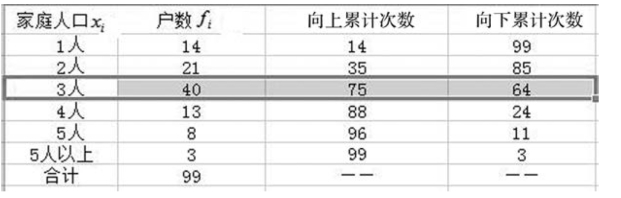
图5-21 某村家庭人口分布资料
解 Σf=99，为奇数，则
按户数向上累计，第50 户在第三组，家庭人口为3 人；向下累计第50 户也包含在第三组，家庭人口为3 人。
②当Σf 为偶数时：
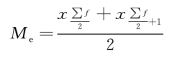
【例5-14】 某村有100 户人家，家庭人口分布资料如图5-22 所示。要求：计算中位数。
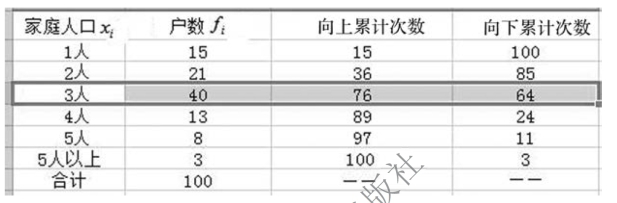
图5-22 某村100 个家庭人口分布资料
解 已知Σf=100，为偶数，则
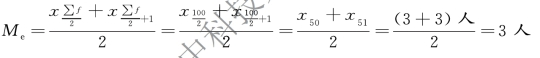
第50 位次与第51 位次均出现在第三组，家庭人口为3 人。
（2）组距式变量数列计算中位数时，根据中位数的定义（中位数是排在中间位次上的单位所对应的标志值），首先，应确定中位数的位次；其次，根据位次确定中位数所在的组，即中位数组，该组的上、下限就规定了中位数的可能取值范围；最后，假定在中位数组内的各单位是均匀分布的，采用比例插入法可求出中位数。
设中位数组的次数为fm，到中位数组前面一组为止的向上累计频数为Sm-1，到中位数组后面一组为止的向下累计频数为Sm+1，L 为中位数所在组的下限，U 为中位数所在组的上限，d=U -L，为中位数组的组距，中位数计算公式如下。
下限公式：
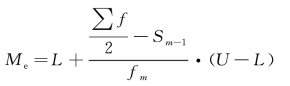
上限公式：
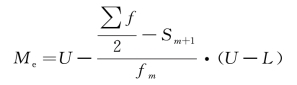
式中，Me 是按比例插入法计算的中位数，是一个近似值。其中，下限公式是根据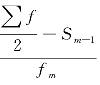
比例分摊“U -L”，上限公式是根据
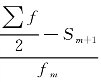比例分摊“U -L”。
【例5-15】 已知某高校100 名学生每月消费支出资料如图5-23 所示。
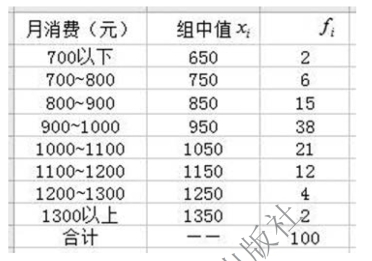
图5-23 某高校100 名学生消费支出资料
要求：根据图5-23 中资料，计算中位数。
解 已知Σf=100，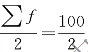
=50，中位数所在组为月消费额900 ～1000 元的组。计算得出中位数组过程如图5-24 所示。
根据下限公式计算：
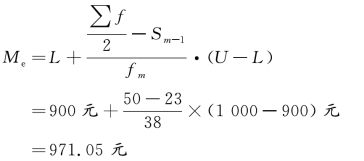
根据上限公式计算：
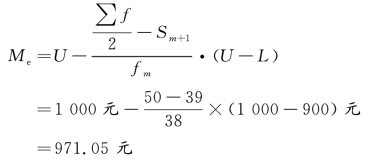
如果该资料按算术平均数计算，则为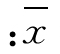
=
=982 元。
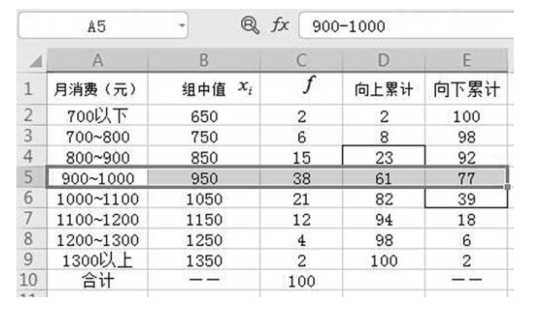
图5-24 中位数组计算得出过程
该高校学生平均每月消费支出为971.05元，比按算术平均数计算出的982元更具代表性。