组距式变量数列的编制
组距式变量数列一般在变量值变动幅度较大的条件下采用,在编制过程中涉及组限、组距、组数等分组要素,下面结合过程与步骤进行说明。
组距式变量数列的一般编制步骤如图3-5 所示。

图3-5 组距式变量数列的一般编制步骤
主要步骤如下:
(1)排序。按一定的顺序排列数据,使数据呈递增或递减趋势,确定最大值与最小值。
(2)计算变异全距。数列中最大值与最小值之差,称为全距,反映现象的变异范围,用R表示:
![]()
式中:Xmax 为最大值;Xmin 为最小值。
(3)确定组数与组距。
确定组数指确定将全部数据分多少组。组距为各组变量值的变动范围或距离。在等距分组时,全距、组距、组数之间的关系为:
![]()
确定组距是编制组距式变量数列的关键问题,需要遵守以下原则:
①要考虑数据资料的集中趋势,将总体分布的特点充分显示出来。首先,对所研究的现象在大量观察的基础上有一个总体的定性认识,了解分布是何种形态;然后,结合资料的实际情况,分析不同区域的数据密集状况,把集中趋势、分布特点表现出来。
②要保证组内同质性,组距是一个区间,同一区间内的单位应是同质的,尽管在数量表现上有差异,但差异很小,不影响对质的判断。
③合理处理组距与组数的关系。在所研究总体一定的情况下,组数的多少和组距的大小是紧密联系的。一般来说,组数和组距成反比关系,即组数少,则组距大;组数多,则组距小。如果组数太多,组距过小,会使分组资料烦琐、庞杂,难以显现总体现象的特征和分布规律;如果组数太少,组距过大,可能会失去分组的意义,达不到正确反映客观事实的目的。在确定组距和组数时,应注意保证各组都能有足够的单位数,组数既不能太多,也不宜太少,应以能充分、准确体现现象的分布特征为宜。
(4)确定组限。从整个数列来看,组限是组与组之间的界限值;从每一组来看,组限是每组区间两端的极值。确定组限,应注意如下几点:
①要能区分各组的性质差异,体现组内资料的同质性和组与组之间资料的差异性。对于一些区分现象不同质的关键值,如计划完成程度的100%是完成与没有完成的分界线,学习成绩60 分是及格与不及格的分界线等,均应作为关键组限。在进行分组时,一般首先选择这些关键组限,再考虑其他因素,根据具体情况进一步细分、观察、调整,做到科学、合理。
②最小组的下限必须包含数列中最小的变量值,即可以是资料中的最小值或小于资料中的最小值;最大组的上限必须包含数列中最大的变量值,即应高于最大的变量值,以便能将所有数据包含进去。
③为了符合习惯和使计算方便,绝对数组距尽可能为5 或10 的整数倍;相对数组距可近似地取10%。
(5)汇总各组单位数。在汇总各组单位数时,为了避免计算上的混乱,一般原则是把到达上限值的标志值计入下一组内,即“上组限不在内”原则。各组单位数,可以用绝对数表示,也可以用相对数表示,即频率(比率、比重)。
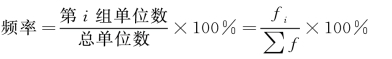
频率的性质为:①任何频率都是界于0 和1 之间的;②各组频率之和等于1。
(6)计算累计频数(频率)。
为了更详细地认识变量的分布特征,还可以计算累计频数和累计频率,编制累计频数和累计频率数列。将变量数列各组的次数和比率逐组累计相加可得累计次数分布,它表明总体在某一标志值的某一水平所包含的总体次数和比率。
累计频数(频率)有向上累计频数(频率)和向下累计频数(频率)两种。
①向上累计频数(频率)。
向上累计频数(频率)是将各组次数和比率,由变量值低的组向变量值高的组逐组累计,表明各组上限以下所包含的总体次数和比率的情况。向上累计会产生相应的向上累计次数和向上累计频率。例如,学生按成绩分组,需要确定某分数以下的学生人数,依次向上累计60 分以下、70 分以下、80 分以下、90 分以下及100 分以下次数和比率,如图3-6 所示。

图3-6 向上累计示意图
②向下累计频数(频率)。
向下累计频数(频率)是将各组次数和比率,由变量值高的组向变量值低的组逐组累计,表明各组下限以上所包含的总体次数和比率的情况。向下累计会产生相应的向下累计次数和向下累计频率。例如,学生成绩统计时,需要确定某一分数以上的学生人数,依次向下累计90 分以上、80 分以上、70 分以上、60 分以上及52 分以上次数和比率,如图3-7 所示。

图3-7 向下累计示意图
(7)制作统计表。用一个统计表将分组结果表现出来。
【例3-3】 某班30 位学生某次考试成绩如下:
76 65 74 82 56 79 74 67 77 70 52 85 76 60 73
87 63 69 98 77 81 84 75 61 74 92 78 73 94 75
要求:编制变量数列。
解 成绩变量值个数较多,但数据分布比较均匀,适宜编制成等距数列。
第一步,数据序列化。
由于这些数据杂乱无章,可按大小顺序,从小到大排列起来,使数据呈现出规律性。结果如图3-8 所示。

图3-8 数据序列化结果
第二步,计算变异幅度,即全距:
![]()
第三步,确定组数。
通过观察,成绩呈现中间部分单位数多,分布密度大,两端依次递减的正态分布,因此,可首先将成绩分为低、中、高三部分,以成绩比较集中的区域为中,左右两边分别确定为低和高,再将低的部分分为低与较低,高的部分分为较高与高。这样就将全距R=46 分成了5 组。
第四步,确定组限、组距。
以60 分作为关键组限,组距取10,第一组的下限为60-10=50<52,其他各组组限(下限)依次为60+10=70,70+10=80,80+10=90,最后一组的上限为90+10=100>98,包含了所有数据。分组结果如图3-9 所示。
![]()
图3-9 分组结果
这样,总共有4 个界限值,所有数据被分成了5 个部分,分别为:50~60 分;60~70 分;70~80 分;80~90 分;90~100 分。
第五步,计算各组次数,累计次数与比率。
第六步,以表格的形式将分组结果显示出来,由于成绩属于连续变量,相邻组组限必须重叠。
编制的变量数列如图3-10 所示。
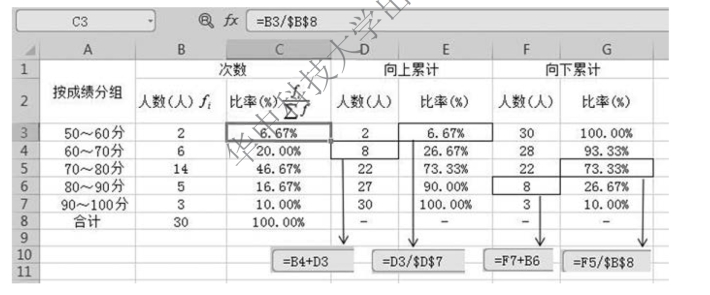
图3-10 考试成绩变量数列编制结果
