一、众数
(一)概念
众数是指一组数据中出现次数最多的变量值,它主要用于测度分类数据的集中趋势,其特点是不受极端值的影响,但仅能反映现象的一般水平。众数用Mo 表示。
(二)特征表现
在频数分布中,众数是频数最大的指标值;从数据的分布层面,它是分布数列中最常出现的标志值;在分配曲线图上,它是曲线的最高峰所对应的标志值。由于没有利用全部数据信息,而且还具有不唯一性,一组数据可能有众数,也可能没有众数;可能有一个众数,也可能有多个众数。数据分布与众数的关系如图5-11 所示。
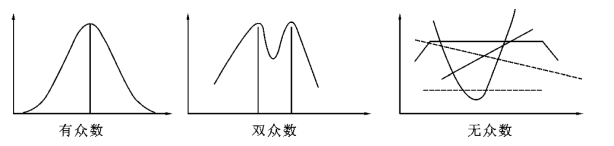
图5-11 数据分布与众数的关系
(三)适用条件
当数据分布存在明显的集中趋势,且有显著的极端值时,适合使用众数;当数据分布的集中趋势不明显(无众数)或存在两个以上分布中心(为双众数或多众数,也等于没有众数)时,不适合使用众数。
(四)众数的计算
根据资料是否分组,众数的计算有所不同。
1.根据未分组数据或单变量值计算众数
未分组数据或单变量值分组数据确定众数时,只需找出次数最多的变量值即可,该变量值即为众数值。步骤如下:
第一步,将标志值由小到大进行排序;
第二步,确定众数。
【例5-9】 某企业某部门10 名职工月工资数据如图5-12 所示。要求:计算平均工资。

图5-12 某部门职工月工资数据
解 从图5-12 中可以看出,职工J 的工资比其他人高出不少,属于极端数值。如果用计算算术平均数的方法计算平均工资,会拉高平均工资,脱离实际情况,不具有代表性,故用众数计算平均工资。工资为3000 元的人数最多,故3000 元就是平均工资。
2.根据组距式变量数列计算众数
当资料中数据可组成组距式变量数列时,首先,确定众数所在组,即次数最大的组(众数组);其次,确定众数所在的位置,众数肯定大于等于该组的下限而小于等于该组的上限,即L ≤Mo ≤U,众数的位置与其相邻组的次数分布有一定的关系,这种关系如图5-13 所示。
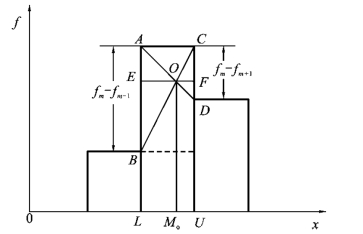
图5-13 组距式变量数列众数的位置与其相邻组的次数分布的关系
图5-13中,fm 为众数组的次数,fm-1 为众数组前一组的次数,fm+1 为众数组后一组的次数。众数组的次数与前一组次数之差表示为fm -fm-1= Δ1;众数组的次数与后一组次数之差表示为fm -fm+1=Δ2,L表示众数组的下限;U表示众数组的上限;d表示众数组的组距,即U-L= d。
当众数组后一组的频数大于众数组前一组的频数时,即fm-1 <fm+1,则众数会向其后一组移动,众数大于众数组组中值。当众数组相邻两组的频数相等时,即fm-1=fm+1,众数组的组中值即为众数;当众数组前一组的频数大于众数组后一组的频数时,即fm-1 >fm+1,则众数会向众数组前一组移动,众数小于众数组组中值。
设Mo 为众数,Mo=L+(Mo -L)或Mo -L= EO,U -Mo=OF。
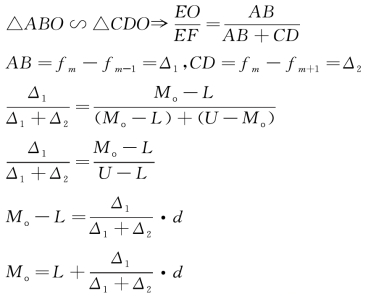
因此,下限公式为:
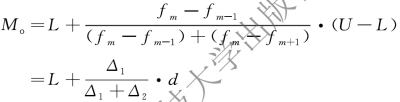
同理,上限公式为:
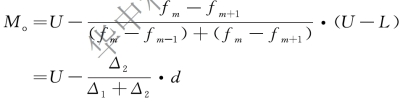
【例5-10】 某企业100 名职工按工资分组统计资料如图5-14所示。要求:计算平均工资。
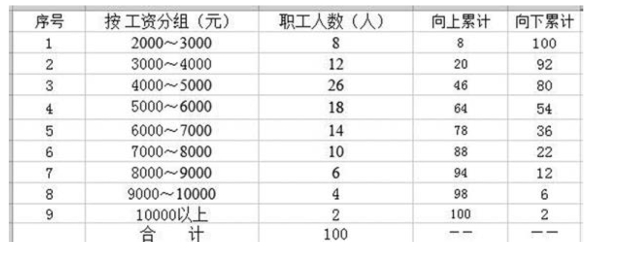
图5-14 某企业100 名职工按工资分组统计资料
解 绘制工资分布图,如图5-15 所示。
从图5-15 中可以看出,工资对应人数呈偏态分布,平均工资用众数计算更具有代表性。步骤如下:
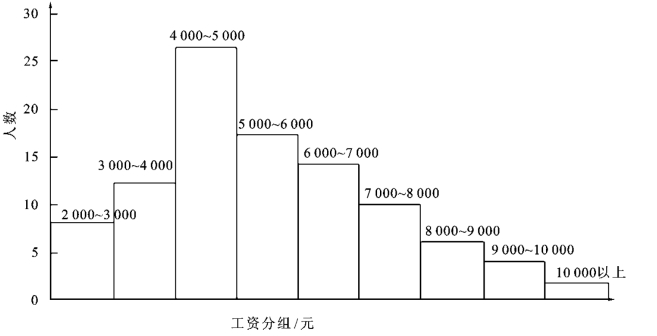
图5-15 工资分布图
第一步,确定众数组,如图5-16 所示。
第二步,计算众数。
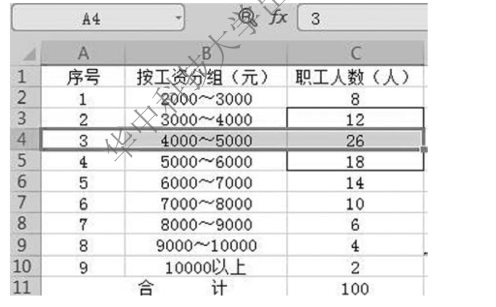
图5-16 确定众数组
已知U= 5000元,L= 4000元,d= 1000元,fm -fm-1= 26人-12人= 14人,fm -fm+1=26 人-18 人= 8 人。
根据下限公式计算:
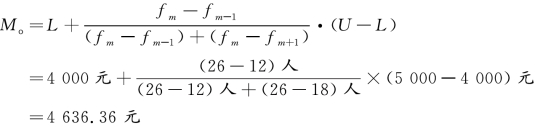
根据上限公式计算:
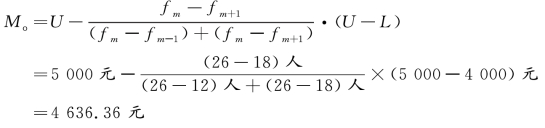
如果按算术平均数计算,则为:
![]()
综上所述,该公司平均工资为4636.36 元,比按算术平均数计算出的5540 元更具代表性。
