四、连环替代法
连环替代法是多因素指数分析法的简化形式，是根据因素之间的内在依存关系，依次测定各因素变动对对象指标差异影响的一种分析方法。
设指数间关系式为y=a×b×c，则连环替代过程为：
如例10-8 中，人工总成本可分解为生产量（a）、工时定额（b）和小时工资（c）三个因素。
基期人工总成本为Σa0b0c0，第一次替代将a0替换为a1，得到Σa1b0c0；第二次在第一次基础上将b0替换为b1，得到Σa1b1c0；第三次在第二次基础上将c0替换为c1，得到报告期总量Σa1 b1c1。将每一次替代后的总量与替代前的总量进行对比，所得指数即为此次被替代因素对人工总成本的影响程度，两个总量的差额也就反映了此次被替代因素对y 的绝对影响量。
第一次替代后与替代前的两个总量对比得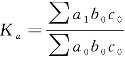
，此比率就是生产量（a）因素的综合变动程度及其对人工总成本影响程度的指数；两者差额Σa1b0c0-Σa0b0c0反映了生产量（a）的变动使人工总成本增减的绝对数量。
第二次替代后与替代前的两个总量对比得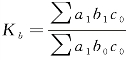
，此比率就是工时定额（b）因素的综合变动程度及其对人工总成本影响程度的指数；两者差额Σa1b1c0-Σa1b0c0反映了工时定额（b）的变动使人工总成本增减的绝对数量。
第三次替代后与替代前的两个总量对比得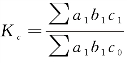
，此比率就是小时工资（c）因素的综合变动程度及其对人工总成本影响程度的指数；两者差额Σa1b1c1-Σa1b1c0反映了小时工资（c）的变动使人工总成本增减的绝对数量。
用最后一次替代结果Σa1b1c1 与基期人工总成本Σa0b0c0 进行对比，得Kabc=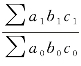
，此比率就是人工总成本指数；两者差额Σa1b1c1-Σa0b0c0反映了人工总成本报告期比基期增减的绝对数量。
相应的指数体系为：
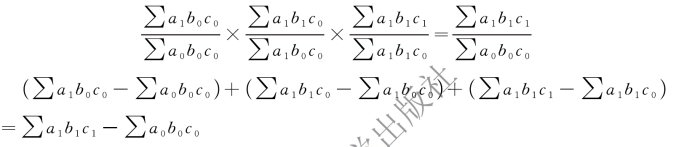
利用连环替代法，能够测定各个因素对分析指标的影响程度，不仅适用于总量指标，也适用于相对指标。在用连环替代法分析相对指标的变动时，主要测算各因素指标变动的绝对差异。
【例10-9】 某公司财务资料如表10-10 所示。
表10-10 财务资料
已知权益资本报酬率=销售经营利润率×资产周转率×财务费用比率×财务结构比率×税收效益比率。要求：计算2018年和2017年相比，权益资本报酬率的变化及各因素变动对权益资本报酬率的影响。
解 设权益资本报酬率为y，销售经营利润率为a，资产周转率为b，财务费用比率为c，财务结构比率为d，税收效益比率为e，则y=a bcde。
使用连环替代法计算过程如图10-5 所示。
2018年权益资本报酬率为：y2018=a1b1c1d1e1=7%×5×0.78×1.8×0.75=36.86%。
2017年权益资本报酬率为：y2017=a0b0c0d0e0=6%×4×0.8×2×0.75=28.8%。
增长率为：y2018 -y2017=36.86% -28.8%=8.06%。
其中：
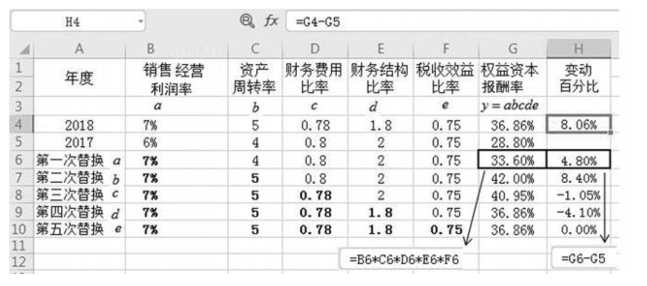
图10-5 连环替代法计算过程
①销售经营利润率的影响为：
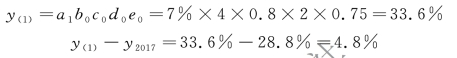
②资产周转率的影响为：
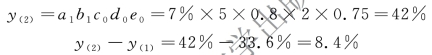
③财务费用比率的影响为：
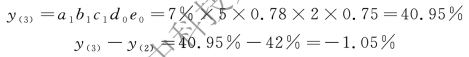
④财务结构比率的影响为：
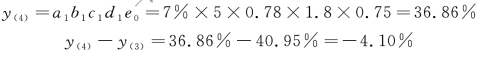
⑤税收效益比率的影响为：
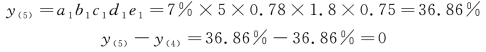
验证：
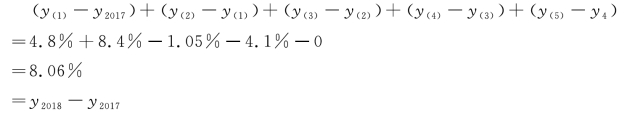
该企业2018 年和2017 年相比，权益资本报酬率增长率为8.06%，其中，销售经营利润率增长了4.8% ；资产周转率增长了8.4%；财务费用比率下降了1.05% ；财务结构比率下降了4.10% ；所得税率没有变化，税收效益比率的增长率为零。
连环替代法不仅适用于动态指数，也适用于静态指数，如对实际成本与标准成本进行比较分析，只需将报告期换为实际成本，将基期换为标准成本即可。