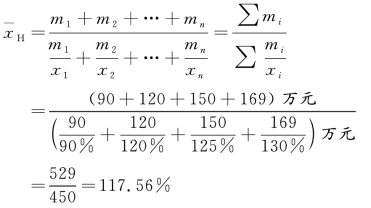二、调和平均数

二、调和平均数

调和平均数是算术平均数的另一种形式，是一组数据中各个变量值倒数的算术平均数的倒数，因而又称为倒数平均数，习惯上用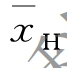 表示。

在实际工作中，经常会遇到资料中只有各组变量值和各组标志总量，缺少单位数的情况，这时就无法直接计算算术平均数，需要根据已知资料推算出单位数，再计算平均数，采用这种计算方法计算出的平均数称为调和平均数。

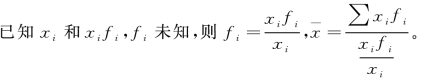
调和平均数分为简单调和平均数和加权调和平均数。

（一）简单调和平均数

式中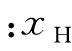 为调和平均数，n 为变量值的个数；xi 为第i 个变量值。

【例5-4】　已知某种时令水果早上每斤10 元（1 斤=500 g），中午每斤8 元，晚上每斤4 元，如果早中晚各买1 元该水果，平均价格为多少？

即平均价格为每斤6.32 元。

（二）加权调和平均数

当各组标志总量不相等时，用加权调和平均数。

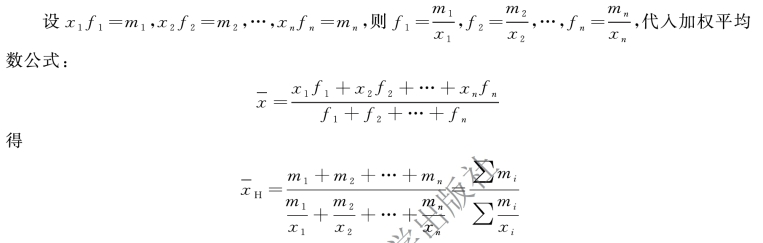
式中：xi 为第i 组的变量值；mi 为第i 组的标志总量。

加权调和平均数适用于总体资料经过分组整理形成变量数列的情况，分为根据平均数计算的加权调和平均数和根据相对数计算的加权调和平均数。

1.根据平均数计算加权调和平均数

【例55】　已知某商品在三个市场的平均价格与销售额统计资料如图5-5 所示，要求计算平均价格。

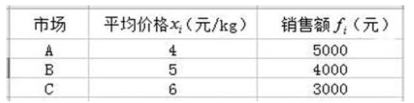
图5-5　某商品在三个市场的平均价格与销售额统计资料

解　平均价格=，由于销售量未知，用调和平均数。计算过程如图5-6 所示。

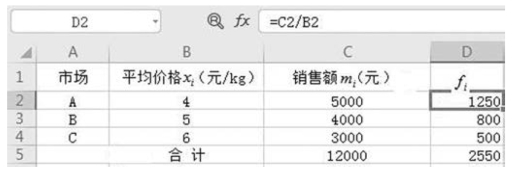
图5-6　平均价格计算过程

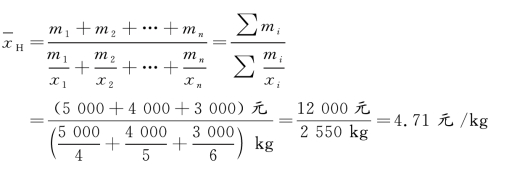
该商品平均价格为4.71 元/kg。

2.根据相对数计算加权调和平均数

【例5-6】　某公司4 个子公司销售计划完成情况如图5-7 所示。要求：计算平均计划完成程度。

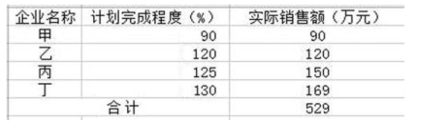
图5-7　某公司子公司销售计划完成情况

解　由于计划完成程度=，计划数未知，用调和平均数计算，计算过程如图5-8所示。

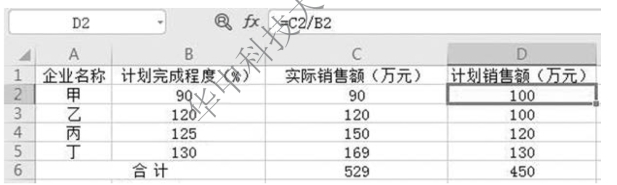
图5-8　平均计划完成程度计算过程