一、算术平均数
算术平均数，又称均值，是统计学中最基本、最常用的一种平均指标，通常用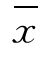
表示。其基本计算公式为：
上式中，分子、分母在内容上属于从属性质，分子是分母的特征值，分母是分子的直接承担者，算术平均数应区别于强度相对指标（强度相对数）。
根据所掌握的数据形式的不同，算术平均数有简单算术平均数和加权算术平均数之分。
（一）简单算术平均数
在总体资料未经分组整理、尚为原始资料的情况下，直接代入算术平均数的基本公式，形成简单算术平均数。
设数据集X=｛x1，x2，…，xn｝，简单算术平均数计算公式为：
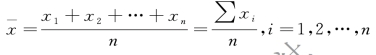
式中：n 为总体单位总数；xi 为第i 个单位的标志值。
【例5-1】 某售货小组5 人某日销售额分别为1100 元、1200 元、1300 元、1400 元、1500元，计算平均每人日销售额。
解 计算过程如下：
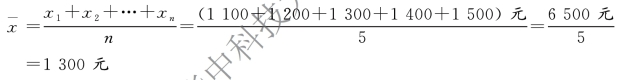
（二）加权算术平均数
在总体资料经过分组、整理形成变量数列的情况下，各组数据次数不再为1，且各不相等，必须首先计算各组标志总量，然后将各组标志总量汇总，才能计算出总体标志总量；再代入算术平均数的基本公式，形成加权算术平均数。
设各组变量值为xi（x1，x2，…，xn），各组次数为fi（f1，f2，…，fn），加权算术平均数计算公式为：
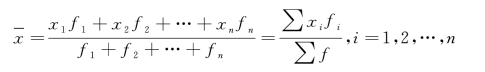
式中：fi 为第i 组的次数；n 为组数；xi 为第i 组的标志值，如果是分组数列，xi 为第i 组的组中值。
【例52】 某企业工人月产量统计资料如图5-1 所示。计算平均每个工人加工零件数。
解 平均每个工人加工零件数为：
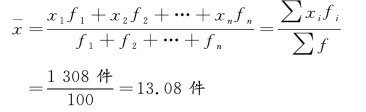
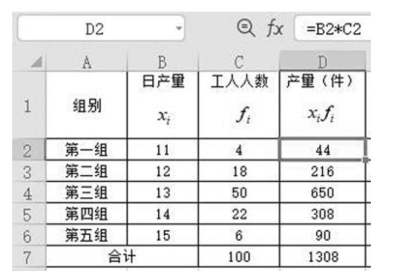
图5-1 某企业工人月产量统计资料
使用Excel 计算平均数步骤：首先，在Excel 表格中输入相关数据；然后，选中数据区域—“公式”—“自动求和”—“平均值”。
1.权数与加权的定义
从例5-2 的计算过程可以看出，加权算术平均数的大小受两个因素的影响：一个是变量xi；另一个是次数fi。在标志值或组中值不变的情况下，各组次数fi 对总体平均数的影响很大，具有权衡轻重的作用，故称权数。
权数（fi）指变量数列中各组标志值出现的次数，是变量值的承担者，反映了各组标志值对平均数的影响程度。
2.权数的表现形式
根据数值的表现形式，权数分为绝对权数和相对权数。
（1）绝对权数，表现为绝对数，如次数、频数、单位数等。在例5-2 中，绝对权数即图5-1 中的工人人数。
（2）相对权数，表现为相对数，如频率、比重，是由绝对数公式进行变形而来。
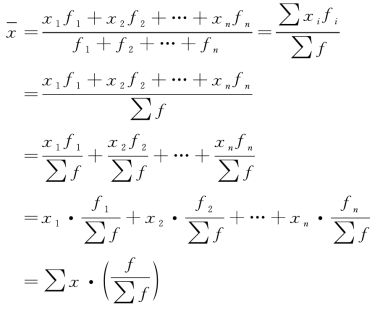
【例53】 某企业某日工人的月产量资料统计如图5-2 所示。要求：按比重计算平均每个工人加工零件数。
解 平均每个工人加工零件数为：
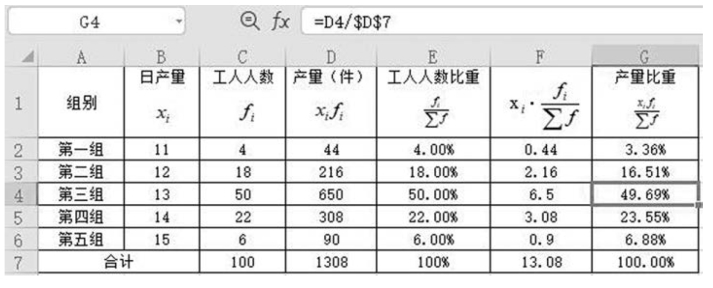
图5-2 某企业某日工人的月产量资料
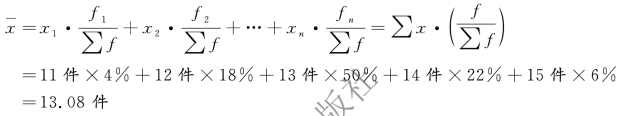
例5-3 计算结果与用绝对数计算的结果（例5-2）相同。这时，平均数演变为各组变量与结构相对数的乘积和，平均数的大小取决于总体结构。
3.权数的作用
权数对平均数具有权衡轻重的作用，通过以下几种情况予以说明。
第一种，如果各组权数相等，则加权算术平均数等于简单算术平均数，因此，简单算术平均数是加权算术平均数的特例。
设f1= f2=…= fn= f，则
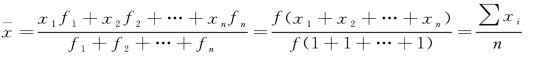
第二种，如果各组权数不相等，在各变量值不变的条件下，哪一组权数大，平均数就趋向哪一组的标志值。
从图5-1 中可以看出，第三组在各组中人数是最多的，因而比重也是最大的，即权数最大，平均数接近第三组，即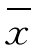
=13.08 件→x3=13 件。
如果将原第三组工人人数与第一组互换，其他不变，这时，第一组权数最大，总人数不变，再观察平均数的变化。所得统计资料如图5-3 所示。
由图5-3 可知，平均每个工人加工零件数为：
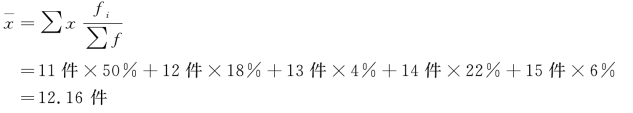
计算结果显示，第一组产量比重变大，平均数即向第一组移动，现在的平均数“12.16 件”比原“13.08 件”小。
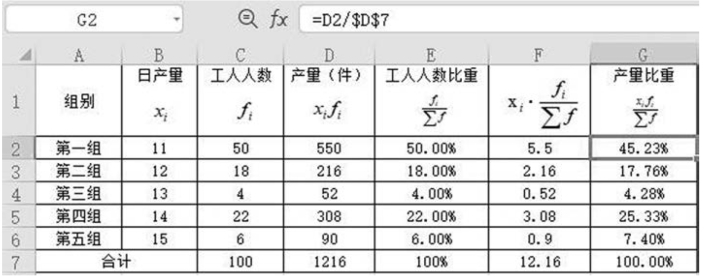
图5-3 第三组工人人数与第一组互换后的月产量统计资料
基于图5-2，如果将第三组工人人数与第五组互换，则第五组权数最大，而总人数不变，再观察平均数的变化。所得统计资料如图5-4 所示。
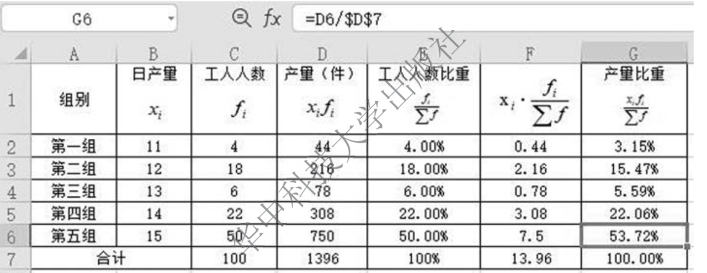
图5-4 第三组工人人数与第五组互换后的月产量统计资料
由图5-4 可知，平均每个工人加工零件数为：
可以看出，第五组产量比重变大，平均数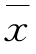
向第五组标志值移动。
从公式和以上计算过程可以看出，加权算术平均数的大小受变量值（xi）和权数（fi）的共同作用：变量值xi 决定平均数的范围；权数fi 则决定平均数的位置或大小，也就是趋中趋势。
4.权数的演变
相对权数在实际中应用更为广泛，当权数为相对数时，很多现象的总体结构相对数在一定期间内变化很小，甚至不变，表现为常数，这时，算术平均数的计算一般采用以下形式。
设变量为ki，总体结构为wj（wj 为常数），加权算术平均数用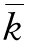
表示，则
这样，平均数的计算变得更为简单。
在实际工作中计算加权算术平均数时，根据需要和实际情况，可以判定哪一部分重要，并给予一个较大的权重再进行计算，反之可给予较小的权重。这种操作称为加权。
（三）算术平均数的主要数学性质
（1）总体单位数与其算术平均数的乘积等于总体标志总量。
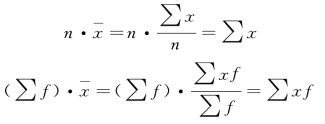
（2）各标志值（xi）与其算术平均数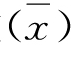
）的离差之和等于零。
①对于简单算术平均数：
式中，Σ（xi-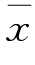
）称为离差，指某一变量值与平均数的距离。
证明过程如下：
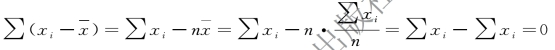
②对于加权算术平均数：
证明过程如下：
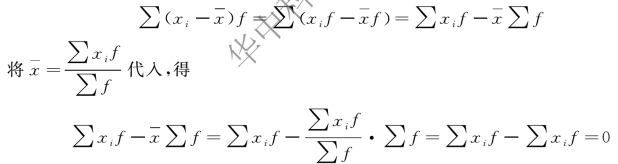
（3）各标志值与其算术平均数的离差平方和具有最小值。
①对于简单算术平均数：
证明：采用反证法，设A 为任意数，假设Σ（x -A）2=最小值，则
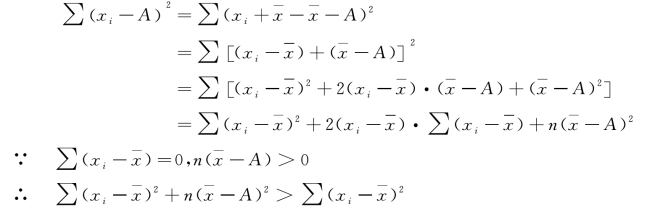
即
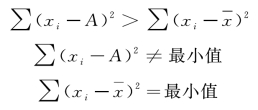
当A=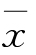
时，Σ（xi -A）2= Σ（xi -
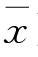）2。
②对于加权算术平均数：
求证方法一样，只需将f 代入展开即可。
（四）算术平均数的应用
（1）算术平均数是根据所有变量值综合计算出来的，属于数值平均数，当数值存在极端数值时，计算出的平均数的代表性就会大打折扣。有时为了提高算术平均数的代表性，通常先在数据中删除极大值和极小值，利用剩余的数据计算算术平均数，这样得到的平均数叫切尾平均数，又称为截尾平均数。
（2）在用组中值作为变量时，由于组中值的计算是假定这一组的变量值均匀分布，带有一定的假定性，计算出的平均数是一个近似值。