二、区间估计
总体参数的区间估计是依照一定的概率保证程度，用样本估计量估计总体参数取值范围的方法。以样本指标为中心，以抽样平均误差为距离单位，可以构造一个区间，并以一定的概率保证待估计的总体参数落在这个区间内。
区间估计必须具备三个基本条件，即样本指标、误差范围和置信度。下面通过一个简单的例子说明这几个概念。
例如，从一个班的学生中随机抽选出5 个学生，经测量，这5 个学生的平均身高为170 cm，平均误差
=10 cm，以此为依据来估计这个班学生的平均身高。
1.样本指标
样本指标中的变量可以是样本平均数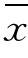
，也可以是样本成数p（在该例中，这5个学生的平均身高的平均误差就是样本指标）。
2.误差范围
误差范围即抽样极限误差，指在一定的概率保证程度上，样本指标与总体指标之间抽样误差的最大可能范围，也称作抽样允许误差，常用
表示。在上例中，这个班的学生的平均身高最大范围即为误差范围。
用数学公式表达误差范围：
即
上式表明，样本平均数（成数）是以总体平均数（成数）为中心，在相应的区间内变动的。这个变动区间叫作置信区间。
总体平均数和总体成数是未知的，要靠实测的抽样平均数和抽样成数来估计，因而抽样误差的实际意义是希望总体平均数（成数）落在某个已知的范围内。所以，前面的不等式应变换为：
在以上案例中，如果允许误差
= 30 cm，则
= 170 cm -30 cm= 140 cm，构成置信下限= 170 cm+30 cm= 200 cm，构成置信上限；置信区间为140～200 cm。这意味着这个班学生的平均身高在140 ～200 cm 范围内。如果允许误差
=10 cm，则
=170 cm -10 cm=160 cm
=170 cm+ 10 cm=180 cm，置信区间为160 ～180 cm。
在一个特定的全及总体中，当抽样方法和样本容量固定时，抽样平均误差是一个定值，因此，抽样极限误差通常以抽样平均误差为标准单位来衡量，即抽样极限误差通常表示为抽样平均误差的多少倍。
由于t 值与样本估计值落入允许误差范围内的概率有关，t 也称为概率度，它表示为了提高可靠性，必须将抽样平均误差扩大至一定的倍数。
抽样极限误差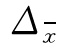
可用概率度t 和抽样平均误差相乘得到：
在以上案例中，允许误差
=30 cm，抽样允许误差就是抽样平均误差
的3倍。在该例中，显然这个班学生的平均身高在140 ～200 cm 范围内的概率要比在160 ～180 cm 范围内的概率大得多。
3.置信度
抽样指标和总体指标的误差不超过一定范围的概率大小，称为概率保证程度，也称抽样估计的置信度，一般用F（t）表示：
式中：P 表示概率，常用P（α）表示不在某个范围的概率，P（1 -α）表示在某个范围的概率。
在以上案例中，这个班学生的平均身高在140 ～200 cm 范围的概率是多少、在160 ～180 cm范围的概率是多少就可以用P 的相关表达式表示。
t 值与相应的概率保证程度存在一一对应的关系，在大样本条件下，常用的t 值及相应的概率保证程度如表6-1 所示。
表6-1 常用的t 值及相应的概率保证程度
概率度t 可以通过查正态分布概率（正态分布曲线下的区间面积比率）得到，如F（t）= 0.9500时，t=1.96，表示要达到95% 的概率保证程度，就必须将抽样平均误差扩大1.96 倍。在以上案例中，这个班学生的平均身高在140 ～200 cm 范围的概率是99.73%，在160 ～180 cm 范围的概率是68.27%。
置信度表达了参数区间估计的可靠性。置信区间越小，说明估计的精确度越高；置信度越大，估计可靠性就越大。一般来说，在样本容量一定的前提下，精确度与置信度往往是相互矛盾的。若置信度增加，则置信区间必然增大，会降低精确度；若精确度提高，则置信区间缩小，置信度必然减小。要同时提高估计的置信度和精确度，就要增加样本容量。